Toán 9 - Tiết 60: Kiểm tra 1 tiết

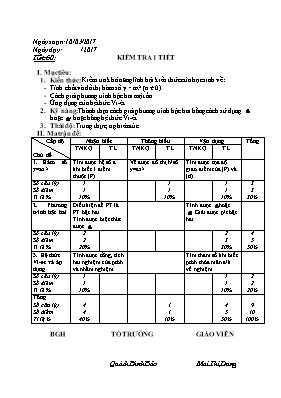
Ngày soạn: 10/03/2017
Ngày dạy: /2017
Tiết 60: KIỂM TRA 1 TIẾT
Mục tiêu:
Kiến thức: Kiểm tra khả năng lĩnh hội kiến thức của học sinh về:
Tính chất và đồ thị hàm số y = ax2 (a ≠ 0) 
Cách giải phương trình bậc hai một ẩn.
Ứng dụng của hệ thức Vi-ét
Kỹ năng: Thành thạo cách giải phương trình bậc hai bằng cách sử dụng hoặc hoặc bằng hệ thức Vi-ét.
Thái độ: Trung thực, nghiêm túc.
Ma trận đề:
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
TNKQ
TL
TNKQ
TL
TNKQ
TL
Hàm số y=ax2
Tìm được hệ số a khi biết 1 điểm thuộc (P)
Vẽ được đồ thị h/số y=ax2
Tìm được tọa độ giao điểm của (P) và (d)
Số câu (ý)
Số điểm
Tỉ lệ %
1
1
10%
1
1
10%
1
1
10%
3
3
30%
2. Phương trình bậc hai
Điều kiện để PT là PT bậc hai.
Tính được biệt thức được 
Tính được hoặc Giải được p/t bậc hai
Số câu (ý)
Số điểm
Tỉ lệ %
2
2
20%
2
3
30%
4
5
50%
3. Hệ thức 
Vi-et và áp dụng
Tính được tổng, tích hai nghiệm của ptbh và nhẩm nghiệm
Tìm tham số khi biết ptbh thỏa mãn đ/k về nghiệm.
Số câu (ý)
Số điểm
Tỉ lệ %
1
1
10%
1
1
10%
2
2
20%
Tổng
Số câu (ý)
Số điểm
Tỉ lệ %
4
4
40%
1
1
10%
4
5
50%
9
10
100%
 BGH TỔ TRƯỞNG GIÁO VIÊN
 Quách Đình Bảo Mai Thị DungTrường THCS Hùng Vương BÀI KIỂM TRA 1 TIẾT
Lớp: 9.. MÔN: ĐẠI 9
Họ và tên: . Thời gian: 45 phút
 Ngày  tháng năm 2017 
ĐIỂM
NHẬN XÉT CỦA GIÁO VIÊN
ĐỀ BÀI:
TRẮC NGHIỆM (4 điểm) Khoanh tròn chữ cái đứng trước câu trả lời đúng.
Câu 1: Đồ thị hàm số y = ax2 đi qua điểm A(5; 2). Khi đó a bằng
A. 
B. 
C. 25
D. 
Câu 2: Phương trình (m + 2)x2 – 2mx + 1 = 0 là phương trình bậc hai khi:
A. m ≠ 1.
B. m ≠ -2.
C. m ≠ 0.
D. mọi giá trị của m.
Câu 3: Phương trình x2 – 3x + 5 = 0 có biệt thức ∆ bằng
A. - 11.
B. -29.
C. -37.
D. 16.
Câu 4: Cho phương trình x2 – 6x – 8 = 0. Khi đó:
A. x1 + x2 = - 6; x1.x2 = 8.
B. x1 + x2 = - 6; x1.x2 = - 8. 
C. x1 + x2 = 6; x1.x2 = 8.
D. x1 + x2 = 6; x1.x2 = - 8.
TỰ LUẬN: (6 điểm).
Bài 1: (3điểm). Giải các phương trình sau:
	a) x2 + 9x + 8 = 0	; 	b) 16x2 – 8x + 1 = 0	
Bài 2: (2điểm). Cho hai hàm số y = x2 và y = x + 2
Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ.
Tìm tọa độ giao điểm của hai đồ thị đó.
Bài 3 : (1điểm). Cho phương trình x2 + 2x + m - 1 = 0	
 Tìm m để phương trình có hai nghiệm x1 ; x2 thỏa mãn điều kiện .
- - - - - - - - - - - - - Hết - - - - - - - - - - - - -
 ĐÁP ÁN VÀ BIỂU ĐIỂM 
Trắc nghiệm
ĐÁP ÁN
Điểm
Câu 1
D
1
Câu 2
B
1
Câu 3
A
1
Câu 4
D
1
Tự luận
ĐÁP ÁN
Điểm
Bài 1
(3 điểm)
x2 + 9x + 8 = 0
( a = 1 ; b = 9; c = 8)
 = 92 – 4.1.8 = 49 ; = 7
Vậy PT có hai nghiệm phân biệt:
 x1 = - 1 ; x2 = - 8
0,5
0,5
0,5
16x2 – 8 x + 1 = 0 
( a = 16 ; b’ = - 4 ; c = 1)
 = (- 4)2 – 16.1 = 0 ; = 1
Vậy PT có nghiệm kép: x1 = x2 = 
0,5
0,5
0,5
Bài 2
(2 điểm)
Vẽ đồ thị hai hàm số y = x2 và y = x + 2 
Hàm số: y = x + 2
x
0
1
y = x + 2
2
3
Hàm số : y = x2 
x
-2
-1
0
1
2
y = x2
4
1
0
1
4
Hoành độ giao điểm của hai đồ thị là:
 x2 = x + 2
 (a = 1 ; b = -1 ; c = - 2)
Vậy PT có hai nghiệm x1 = -1 ; x2 = 2
Với x1 = -1 y1 = (-1)2 = 1 
Với x2 = 2 y2 = 22 = 4 
Tọa độ giao điểm của hai đồ thị 
	A(-1; 1); 	B(2; 4)
0,5
0,5
0,5
0,5
Bài 3
(1 điểm)
 PT: x2 + 2x + m - 1 = 0	
 (a = 1 ; b’ = 1 ; c = m -1)
 = 12 – 1.(m - 1) = 2 - m
Phương trình có nghiệm 02 – m0m2
Theo hệ thức Vi-Ét: 
Và ta có: x1 – x2 = 4 (3)
Từ (1) và (3) ta có hệ: 
Thay giá trị của x1, x2 vào (2) m = -2 (tmđk)
Vậy với m = - 2 thì phương trình đã cho có 2 nghiệm thỏa mãn điều kiện .
0,25
0,25
0,25
0,25
Lưu ý: Cách làm khác đúng vẫn cho điểm tối đa.