Ôn tập Toán khối 7

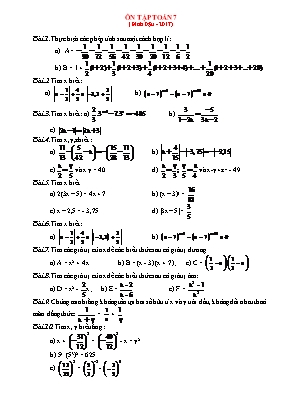
ÔN TẬP TOÁN 7
(Đinh Dậu - 2017)
Bài 1. Thực hiện các phép tính sau một cách hợp lí:
A= 
B = 1+ 
Bài 2. Tìm x biết: 
 a) 	b) 
Bài 3. Tìm x biết: a) 	b) 
c) 
Bài 4. Tìm x,y,z biết :
a) ; 	b) 
 	c) và x.y = 40 	d) và x-y+ z= - 49
Bài 5. Tìm x biết
a) 2(3x – 5) = 4x + 7 	b) (x – 3)4 = 
c) x – 2,5 = - 3,75 	d) |3x – 5| = 
Bài 6. Tìm x biết:
a) 	b) 	
Bài 7. Tìm các giá trị của x để các biểu thức sau có giá trị dương.
a) A = x2 + 4x 	b) B = (x - 3) (x + 7) ; 	c) C = 
Bài 8. Tìm các giá trị của x để các biểu thức sau có giá trị âm:
a) D = x2 - x ; 	b) E =	c) F = 
Bài 9. Chứng minh rằng không tồn tại hai số hữu tỉ x và y trái dấu, không đối nhau thoả mãn đẳng thức: = + 
Bài 10. Tìm x, y biết rằng:	
a) x + = - x = y2 	
b) 5x. (53)2 = 625 	
c) = - 	
Bài 11. Tìm x biết:
a) (5x + 1)2 = 	b) = 
c) (8x - 1)2n+1 = 52n+ 1 	(n Î N)
d) x2 + = 0 	 	e) + ≤ 0
Bài 12. Tìm x, y Î Z biết: 
a) 25 – = 8( x – 2009)	b) = + 1997	c) x + y + 9 = xy – 7.
Bài 13.
a) Tìm GTNN của biểu thức A = - 1
	b) Tìm GTLN của biểu thức B = + 3
Bài 14. Cho x + y = 2. Chứng minh rằng xy ≤ 1
Bài 15. Tìm các số x, y, z biết:
a) = = và x - 3y + 4z = 62; 	b) = ; = và x - y + z = -15
c) = ; = và 2x + 5y - 2z = 100
Bài 16.
a) Tìm x, y, z biết = = và x + y + z = 486. 
b) Tìm x, y, z biết: = = và xyz = 20
Bài 17. Tìm x, y, z biết: = = và x2 + y2 - z2 = 585
Bài 18. a) Cho 
Chứng minh rằng: 
b) Cho . Cmr: m, n, p lần lượt tỉ lệ với x, y, z 
Bài 19. Cho = (a ≠ 5; b ≠ 6). Chứng minh rằng = 
Bài 20. Chứng minh rằng nếu = thì = 
Bài 21. Ba kho có tất cả 710 tấn thóc. Sau khi chuyển đi số thóc ở kho I, số thóc ở kho II và số thóc ở kho III thì số thóc còn lại ở ba kho bằng nhau. Hỏi lúc đầu mỗi kho có bao nhiêu tấn thóc ?
Bài 22. Một khu vườn hình chữ nhật có diện tích là 300m2, hai cạnh tỉ lệ với 4 và 3. Tính chiều dài, chiều rộng khu vườn.
Bài 23. Tìm hai phân số tối giản biết hiệu của chúng là , các tử tỉ lệ với 3 và 5; các mẫu tương ứng tỉ lệ với 4 và 7.
Bài 24. Cho dãy tỉ số bằng nhau:
 = = = 
Tìm giá trị của biểu thức M, biết M = + + + 
Bài 25. Cho = ≠ ± 1 và c ≠ 0. Chứng minh rằng:
a) = 	b) = 
Bài 26. Cho b2 = ac ; c2 = bd. Với b, c, d ≠ 0 ; b + c ≠ d ; b3 + c3 ≠ d3
Chứng minh rằng: = 
Bài 27. Cho b2 = ac Chứng minh rằng = 
Bài 28. Cho = với a, b, c, d ≠ 0; c ≠ ± d. C.minh rằng = hoặc = 
Bài 29. Cho = = . Chứng minh rằng 
Bài 30. 
a) Số A được chia thành 3 số tỉ lệ theo . Biết rằng tổng các bình phương của ba số đó bằng 24309. Tìm số A.
b) Cho . Chứng minh rằng: 
Bài 31. Ba trường A, B, C cùng mua một số gói tăm từ thiện, lúc đầu số gói tăm dự định chia cho ba trường tỉ lệ với 5:6:7 nhưng sau đó chia theo tỉ lệ 4:5:6 nên có một trường nhận nhiều hơn dự định 40 gói. Tính tổng số gói tăm mà ba trường đã mua.
Bài 32. Cho 100 số hữu tỉ trong đó tích của bất kỳ ba số nào cũng là một số âm. Chứng minh rằng:
a) Tích của 100 số đó là một số dương. 
b) Tất cả 100 số đó đều là số âm.
Bài 33. Một số M được chia làm 3 phần sao cho phần thứ nhất và phần thứ hai tỉ lệ (thuận) với 5 và 6; phần thứ hai và phần thứ ba tỉ lệ (thuận) với 8 và 9. Biết phần thứ ba hơn phần thứ hai là 150. Tìm số M.
Bài 34. Một đội thuỷ lợi có 10 người làm trong 8 ngày đào đắp được 200m3 đất. Một đội khác có 12 người làm trong 7 ngày thì đào đắp được bao nhiêu mét khối đất ? (Giả thiết năng suất của mỗi người đều như nhau).
Bài 35. Vận tốc riêng của một ca nô là 21km/h, vận tốc dòng sông là 3km/h. Hỏi với thời gian để ca nô chạy ngược dòng được 30km thì ca nô chạy xuôi dòng được bao nhiêu km?
Bài 36. Một ô tô chạy từ A đến B với vận tốc 65km/h, cùng lúc đó một xe máy chạy từ B đến A với vận tốc 40km/h. Biết khoảng cách AB là 540km và M là trung điểm của AB. Hỏi sau khi khởi hành bao lâu thì ô tô cách M một khoảng bằng khoảng cách từ xe máy đến M.
Bài 37. Tìm 3 phân số tối giản biết tổng của chúng là 3, tử của chúng tỉ lệ với 2, 3, 5 còn mẫu tỉ lệ với 5, 4, 6.
Bài 38. Hai cạnh của một tam giác dài 25cm và 36cm. Tổng độ dài hai đường cao tương ứng là 48,8cm. Tính độ dài của mỗi đường cao nói trên.
Bài 39. Một xe ô tô chạy từ A đến B gồm 3 chặng đường dài bằng nhau nhưng chất lượng mặt đường tốt xấu khác nhau. Vận tốc trên mỗi chặng lần lượt là 72km/h; 60km/h; 40km/h. Biết tổng thời gian xe chạy từ A đến B là 4 giờ. Tính quãng đường AB.
Bài 40. Một ô tô dự định chạy từ A đến B trong một thời gian nhất định. Nếu xe chạy với vận tốc 64km/h thì đến nơi sớm được 1 giờ. Nếu xe chạy với vận tốc 63km/h thì đến nơi sớm được 2 giờ. Tính quãng đường AB và thời gian dự định đi.
Bài 41. Điều tra về số con của 20 hộ thuộc một thôn được cho trong bảng sau:
2
2
2
2
2
3
2
1
0
3
4
5
2
2
2
3
1
2
0
1
a) Dấu hiệu cần tìm hiểu ở đây là gì? b) Lập bảng “tần số”;
c) Tính số trung bình cộng và tìm mốt của dấu hiệu.
Bài 42. Điểm kiểm tra một tiết của lớp 7A được ghi lại như sau:
7
6
5
6
4
8
4
7
6
8
10
8
3
8
9
6
7
8
7
9
8
7
9
7
8
10
5
4
8
5
a) Lập bảng tần số 	b) Tính chung bình cộng và tìm Mo
Bài 43. T×m hiÓu thêi gian (®¬n vÞ: phót) lµm mét bµi tËp cña häc lớp 7 ngêi ta lËp ®îc b¶ng sau:
Thêi gian
3
4
5
6
7
8
9
10
11
12
Sè HS
1
3
5
9
6
4
3
2
1
1
N =35
a) Dấu hiÖu ë ®©y lµ g×?
b) TÝnh thêi gian trung b×nh làm một bài tập cña học sinh líp 7.
c) NhËn xÐt vÒ thêi gian lµm bµi tËp cña học sinh so víi thêi gian trung b×nh làm một bài toán
4	5	6	7	6	7	6	4
6	7	6	8	5	6	9	10	
5	7	8	8	9	7	8	8	
8	10	9	11	8	9	8	9
4	6	7	7	7	8	5	8	
Bài 44. Thời gian làm bài tập của các học sinh lớp 7 tính bằng phút đươc thống kê bởi bảng sau:
a) Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b) Lập bảng tần số? Tìm mốt của dấu hiệu? Tính số trung bình cộng? 
c) Vẽ biểu đồ đoạn thẳng?
Bài 45. Điểm kiểm tra học kỳ môn Toán của các học sinh nữ trong một lớp được ghi lại trong bảng sau:
	5	6	8	7	6	 9	8	10	 9	 7	9	5	6	8	9	10	8	7 4 8
a) Dấu hiệu ở đây là gì? Lập bảng tần số các giá trị của dấu hiệu.
b) Tính số trung bình cộng và tìm mốt của dấu hiệu.
BÀI TẬP HÌNH HỌC
Bài 46. Cho ABC vuoâng taïi A coù AB = 8cm, AC = 6cm.
a) Tính BC.
b) Treân caïnh AC laáy ñieåm E sao cho AE = 2cm , treân tia ñoái cuûa tia AB laáy ñieåm D sao cho AD = AB. Chöùng minh BEA = DEA
c) Chöùng minh raèng DE ñi qua trung ñieåm caïnh BC.
Bài 47. Cho ABC nhọn, có BC = a, CA = b, AB = c. Gọi M là một điểm thuộc miền trong của tam giác. Hạ MH, MK, MP lần lượt vuông góc với BC, CA, AB.
 	a) Chứng minh : AP2 + BH2 + CK2 = BP2 + CH2 + AK2.
 	b) Tìm giá trị nhỏ nhất của: AP2 + BH2 + CK2 (tính theo a,b,c)
Bài 48. Cho ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a) AC = EB và AC // BE
 	b) Gọi I là một điểm trên AC; K là một điểm trên EB sao cho AI = EK. Chứng minh ba điểm I , M , K thẳng hàng
 	c) Từ E kẻ . Biết = 50o ; =25o.Tính và 
Bài 49. Cho ABC cân tại A có , vẽ tam giác đều DBC (D nằm trong tam giác ABC). Tia phân giác của cắt AC tại M. Chứng minh:
a) Tia AD là phân giác của 
b) AM = BC
Bài 50. Cho ABC đều, phân giác BD và CE cắt nhau tại O. Chứng minh rằng:
a) BD ^ AC và CE ^ AB 
b) OA = OB = OC
c) = = từ đó suy ra số đo của mỗi góc ấy.
Bài 51. Cho O là trung điểm của AB. Trên hai nửa mặt phẳng đối nhau bờ AC, vẽ các tia Ax và By cùng vuông góc với AB. Lấy điểm M trên tia Ax, điểm N trên tia By sao cho AM = BN. Chứng minh rằng O là trung điểm của MN.
Bài 52. Cho DABC vuông tại A có = 45o. Vẽ phân giác AD. Trên tia đối của tia AD lấy điểm E sao cho AE = BC. Trên tia đối của tia CA lấy điểm F sao cho CF=AB.
Chứng minh rằng BE = BF và BE ^ BF
Bài 53. Cho DABC. Các điểm D và M di động trên cạnh AB sao cho AD = BM. Qua D và M vẽ các đường thẳng song song với BC cắt cạnh AC lần lượt tại E và N. Chứng minh rằng tổng DE + MN không đổi.
Bài 54. Cho DABC, , phân giác BD và CE cắt nhau tại O. Trên cạnh BC lấy hai điểm I và K sao cho = = 30o. Chứng minh rằng:
a) OI ^ OK 	
b) BE + CD < BC
Bài 55. Cho DABC. Vẽ ra phía ngoài của tam giác này các tam giác vuông cân ở A là ABE và ACF. Vẽ AH ^ BC. Đường thẳng AH cắt EF tại O. Chứng minh rằng O là trung điểm của EF.
Bài 56. Cho DABC, . Vẽ các đường cao BD và CE. Trên tia đối của tia BD lấy điểm I, trên tia đối của tia CE lấy điểm K sao cho BI = AC và CK = AB. Chứng minh rằng DAIK vuông cân.
Bài 57. Cho , điểm A trên tia Ox, điểm B trên tia Oy. Lấy điểm E trên tia đối của tia Ox, điểm F trên tia Oy sao cho OE = OB; OF = OA
a) Chứng minh rằng AB = EF và AB ^ EF
b) Gọi M và N lần lượt là trung điểm của AB và EF. Chứng minh rằng DOMN vuông cân.
Bài 58. Cho DABC. Qua A vẽ đường thẳng xy//BC. Từ điểm M trên cạnh BC vẽ các đường thẳng song song với AB, AC chúng cắt xy theo thứ tự tại D và E. Chứng minh rằng:
a) DABC = DMDE 
b) Ba đường thẳng AM, BD, CE cùng đi qua một điểm.
Bài 59. Cho ABC nhọn, = 60o, đường cao BD. Gọi M, N lần lượt là trung điểm của AB, AC. 
a) Xác định dạng của các tam giác BMD, AMD
b) Trên tia AB lấy điểm E sao cho AE = AN. Chứng minh CE ^ AB
Bài 60. Cho DABC vuông cân tại A. Vẽ ra ngoài DABC tam giác cân BCM có đáy BC và góc ở đáy 15o. Vẽ ABN đều (N thuộc nửa mặt phẳng bờ AB có chứa C). Chứng minh rằng ba điểm B, M, N thẳng hàng.
Bài 61. Cho DABC vuông tại A. Trên cạnh BC lấy hai điểm M và N sao cho BM = BA; CN = CA. Tính .
Bài 62. Cho ABC vuông tại A (AB < AC), phân giác AD. Từ D vẽ một đường thẳng vuông góc với BC cắt AC tại M. Tính .
Bài 63. Cho ABC có = 75o; = 60o. Kéo dài BC một đoạn thẳng CD sao cho CD = BC. Tính .
Bài 64. Cho ABC có < 900 và. Kẻ đường cao AH. Trên tia đối của tia BA lấy điểm E sao cho BE = BH. Đường thẳng HE cắt AC tại D.
a) Chứng minh .	
b) Chứng minh DH = DC = DA.
	c) Lấy B’ sao cho H là trung điểm của BB’. Chứng minh AB’C cân.
	d) Chứng minh AE = HC.
Bài 65. Cho ABC có đường trung tuyến AM, AB = 6cm, AC = 8cm, và AM = cm.
	a) Tính số đo góc BAC
	b) Tính BC
	c) Tính diện tích tam giác ABC. 
Bài 66. Cho ABC. Trung tuyến BM và đường phân giác CD cắt nhau tại I thỏa mãn IB = IC. Từ A kẻ AH BC. Chứng minh rằng IM = IH.
Bài 67. Cho ABC có góc BAC bằng 105o, đường phân giác trong CD và đường trung tuyến BM cắt nhau tại K thỏa mãn KB = KC. Gọi H là chân đường cao hạ từ A của tam giác ABC.
	a) Chứng minh rằng HA = HB
	b) Tính .
Bài 68. Cho ABC cân. Trên cạnh đáy BC lấy điểm D sao cho CD = 2BD. So sánh số đo và .
Bài 69. Gọi P là trung điểm cạnh BC của ABC và BE, CF là hai đường cao. Đường thẳng qua A, vuông góc với PE, cắt đường thẳng BE tại N. Gọi K và G lần lượt là trung điểm của BM và CN. Gọi H là giao điểm của đường thẳng KF là GE. CMR: AH EF.
Bài 70. Cho DEF vuông tại D, có EK là phân giác. Kẻ KM EF, kéo dài KM cắt đường thẳng DE tại I. Chứng minh:
a) DK = KM ; DE = EM.
b) EK IF.
c) Nếu cho M là trung điểm của EF. Chứng minh: .