Ôn tập môn Hình học 10 (cơ bản)

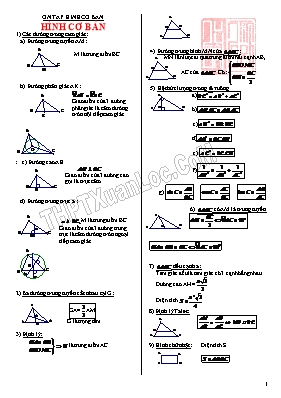
ON TAP HINH CO BAN
HÌNH CƠ BẢN 
 1) Các đường trong tam giác:
 a) Đường trung tuyến AM:
 M là trung điểm BC
 b) Đường phân giác AK: 
Giao điểm của 3 đường phân giác là tâm đường trịn nội tiếp tam giác
 : c) Đường cao AH
Giao điểm của 3 đường cao gọi là trực tâm
 d) Đường trung trực a :
 M là trung điểm BC
Giao điểm của 3 đường trung trực là tâm đường trịn ngoại tiếp tam giác
 2) Ba đường trung tuyến cắt nhau tại G: 
 GA=AM
 G là trọng tâm
 3) Định lý: 
 là trung điểm AC
 4) Đường trung bình MN của :
 MN lần lượt đi qua trung điểm hai cạnh AB, AC của . Cĩ: 
 5) Hệ thức lượng trong vuơng
a)
b)
 c)
 d)
 e) 
 f)
 g) ; ; 
 6) cĩ AM là trung tuyến 
7) đều cạnh a: 
 Tam giác đều là tam giác cĩ 3 cạnh bằng nhau
 Đường cao AH =
 Diện tích 
8) Định lý Talet: 
9) Hình chữ nhật: Diện tích S
10) Hình vuơng:
11) vuơng
12) Tam giác thường
13) Hình thang 
14) Hình bình hành
15) Hình thoi
, 
16) Hình trịn: 
17 ) Tam giác, tứ giác
 a) Tổng hai cạnh của 1 lớn hơn cạnh thứ ba
 b) Hiệu hai cạnh của 1 nhỏ hơn cạnh thứ ba
 c) Gĩc ngồi của 1 
 d) Tổng 3 gĩc trong 1 bằng 1800
 e) Tổng 4 gĩc trong 1 tứ giác bằng 
 Các phương pháp chứng minh
18) CM 2 bằng nhau
 a) Tam giác thường (3 cách)
 (c-g-c), (g-c-g), (c-c-c)
 b) vuơng (5 cách)
 (c-g-c), (g-c-g), (c-c-c)
 Cạnh huyền, 1 cạnh gĩc vuơng
 Cạnh huyền, 1 gĩc nhọn
19) CM cân 
 a) 2 cạnh bằng
 b) 2 gĩc bằng
 c) 1 đường cĩ 2 trong 3 tính chất: cao, phân giác, trung tuyến
 3) CM đều
 a) 3 cạnh bằng
 b) 3 gĩc bằng
 c) cân, cĩ 1 gĩc bằng 
20) CM hình thang: 
 CM tứ giác cĩ 2cạnh //
21) CM hình thang cân( 2 gĩc ở 1 đáy bằng nhau)
 CM tứ giác là hình thang cĩ:
 a) Hai gĩc kề 1 đáy bằng nhau
 b) Hai gĩc đối bù nhau (tổng bằng 1800)
 c) Hai đường chéo bằng nhau
22) CM tứ giác là hbh
 a) 2 cặp cạnh đối song song
 b) 2 cặp cạnh đối bằng nhau
 c) 1 cặp cạnh đối song song và bằng nhau
 d) 2 cặp gĩc đối bằng nhau 
 e) 2 đường chéo cắt nhau tại trung điểm của mỗi đường
23) CM tứ giác là hình thoi: 
 CM tứ giác
 a) là hbh cĩ 2 cạnh liên tiếp bằng nhau
 b) là hbh cĩ 2 đường chéo vuơng gĩc
 c) là hbh cĩ 1 đường chéo là phân giác của gĩc cĩ đỉnh thuộc đường chéo ấy 
 d) cĩ 4 cạnh bằng nhau
 e) cĩ mỗi đường chéo của tứ giác là phân giác của gĩc cĩ đỉnh thuộc đường chéo ấy
24) CM tứ giác là hcn: CM tứ giác
 a) là hbh cĩ 1 gĩc vuơng
 b) là hbh cĩ 2 đường chéo bằng nhau
 c) cĩ 3 gĩc vuơng
 d) là hình thang cân cĩ 1 gĩc vuơng
25) CM tứ giác là hình vuơng: CM tứ giác
 a) là hình thoi cĩ 1 gĩc vuơng
 b) là hình thoi cĩ 2 đường chéo bằng nhau
 c) là hcn cĩ 2 cạnh liên tiếp bằng nhau
 d) là hcn cĩ 2 đường chéo vuơng gĩc
26) CM 1 đường thẳng là tiếp tuyến của 1 đường trịn: CM đường thẳng đĩ vuơng gĩc với bán kính tại đầu mút của bán kính
OB là bán kính đường trịn
aOB tại B
Vậy a là tiếp tuyến của đường trịn (O)
27) CM 2 đoạn thẳng bằng nhau:
 a) CM 2 bằng nhau
 b) Cùng bằng cạnh thứ ba
 c) 
 d) Tổng (hay hiệu) của hai cặp đoạn thẳng bằng nhau từng đơi một thì bằng nhau
 e) cĩ 2 gĩc = cân 2 cạnh bằng nhau
 f) cân đường phân giác hay đường cao ở đỉnh chia đơi cạnh đáy
 g) Áp dụng đl I)3
 h) Tính chất đoạn chắn
 i) CM tứ giác là hbh 2 cạnh đối bằng nhau
 j) vuơng tại A cĩ AM là trung tuyến
 k) Khoảng cách từ tâm đến 2 dây cung bằng nhau thì 2 dây cung bằng nhau
 l) Giao điểm 2 tiếp tuyến trong 1 đường trịn cách đêu 2 tiếp điểm
 AB = AC
 m) 
28) CM 2 gĩc bằng nhau:
 a) CM 2 bằng nhau
 b) cĩ 2 cạnh bằng cân 2 gĩc bằng
 c) cân thì đường cao hay trung tuyến cũng là phân giác
 d) 2 cặp gĩc bằng đồng dạng cặp gĩc thứ ba bằng
 e) 2 gĩc đối đỉnh 
 f) 2 đường thẳng song song bị chắn bởi đường thẳng thứ ba 2 gĩc so le trong bằng nhau, 2 gĩc đồng vị bằng 
 g) 2 gĩc (cùng nhọn hoặc cùng tù) cĩ cạnh đơi một song song
 h) 2 gĩc (cùng nhọn hoặc cùng tù) cĩ cạnh đơi một vuơng gĩc
 i) cùng bằng gĩc thứ ba
 j) cùng phụ (hoặc cùng bù) với gĩc thứ ba
 k) cùng cộng với gĩc thứ ba bằng 
 l) 
 m) 2 gĩc là tổng (hay hiệu) của 2 gĩc bằng nhau từng đơi một
 n) CM tứ giác là hbh 2 gĩc đối bằng nhau
 o) Hai tiếp tuyến cắt nhau
29) CM 2 đường thẳng song song:
a) 2 gĩc so le trong bằng nhau 2 đt //
b) 2 gĩc đồng vị bằng nhau 2 đt //
c) 2 gĩc trong (hoặc ngồi) cùng phía bù nhau 2 đt //
d) 2 đt cùng // với đt thứ ba 2 đt //
 e) 2 đt cùng với đt thứ ba 2 đt //
 f) CM tứ giác là một trong các hình: hbh, hcn, h.thoi, h.vuơng 2 cạnh đối //
 g) Đường trung bình trong một thì // với cạnh thứ ba
 h) Áp dụng đl Ta let đảo mục I) 7)
30) CM 2 đường thẳng vuơng gĩc với nhau
 a) 2 đt giao nhau tạo thành 2 gĩc kề = 2 đt 
 b) 2 đt tạo thành gĩc 900, mục I) 6)
 c) cĩ 2 gĩc phụ nhau gĩc cịn lại bằng 2đt 
 d) 
 e) a // c, b // d, cd 
 f) cân đ.phân giác hay trung tuyến cũng là đcao
 g) 2 tia phân giác của hai gĩc kề bù thì vuơng gĩc 
 h) Định lý Pitago đảo
 i) Đường cao thứ 3 trong 1
 j) Đường kính qua trung điểm 1 dây khơng qua tâm đường kính dây cung
 k) Tiếp tuyến bán kính đi qua tiếp điểm
 l ) 2 cạnh của gĩc nội tiếp chắn nửa đường trịn
31 ) CM 3 điểm thẳng hàng
 a) A, B, C thẳng hàng
 b) A, B, C thẳng hàng
 c) A, B, C thẳng hàng 
 d) A, B, C thẳng hàng
 e) Định lý về các đường đồng quy trong 1 
 f) Đường trịn (O) cĩ AB là đường kính A, O, B thẳng hàng
 g) Đường trịn (O) và (O’) tiếp xúc nhau tại A O, A, O’ thẳng hàng 
32) CM 4 điểm nằm trên 1 đường trịn
 a) CM 4 điểm cách đều 1 điểm nào đĩ
 b) CM 4 điểm là 4 đỉnh của hình thang cân, hcn, h.vuơng
 c) CM là đỉnh của tứ giác cĩ tổng 2 gĩc đối bằng 1800
 d) 2 điểm M, N cùng nhìn đoạn AB dưới 1 gĩc vuơng
 e) 2 điểm M, N cùng nhìn đoạn AB dưới 1 gĩc 
 HÌNH 10
33) Quy tắc hình bình hành 
34) Quy tắc ba điểm: 
35) Quy tắc trừ: 
36) I là trung điểm AB 
37) G là trọng tâm 
38) Hai vectơ bằng nhau: 
39) Toạ độ của vt: Cho A(xA;yA) và B(xB;yB)
 =(xB-xA ; yB-yA)
40) Toạ độ trung điểm I của đoạn thẳng AB:
 A(xA;yA), B(xB;yB) 
 xI= , yI = 
41) Toạ độ trọng tâm G(xG ;yG ) của 
 xG =, yG =
42) Tích vơ hướng của hai véctơ 
43) Tam giác ABC
44) Biểu thức toạ độ của tích vơ hướng 
45) Độ dài của vectơ
46) Gĩc giữa hai vectơ
 Cos() ==
47) Khoảng cách giữa hai điểm
 AB =
48) Định lý Cơ sin 
 a2 = b2 + c2 -2bc cosA
 b2 = a2 + c2 -2ac cosB
 c2 = a2 + b2 -2ab cosC
49) Độ dài đường trung tuyến
ma2 = 
mb2 =, 
 mc2 =
50) Định lý sin: 
51) Diện tích tam giác
 a) S = ab sinC = bc sinA = ac sinB,
 b) S = , 
 c) S = pr,
 d) S = 
Trong đĩ p = , 
 r là bán kính đường trịn nội tiếp
 R là bán kính đường trịn ngoại tiếp
52) Phương trình tham số của đường thẳng 
 qua M0(x0;y0) và nhận làm vtcp ( song song hoặc trùng )
53)Phương trình tổng quát của đường thẳng 
 a(x –x0) +b(y –y0) = 0
 qua M0(x0;y0) và nhận làm vtpt ( vuơng gĩc với )
54) Vtcp nên=(c;d) =( -d;c)
55) Gĩc giữa hai đường thẳng 
 : a1x +b1y +c = 0
 : a2x +b2y +c = 0 cos===
Trong đĩ , 
Chú ý: a)
 b) và 
56) Khoảng cách từ điểm M0 đến đường thẳng 
 d ( M0;) =
57)Phương trình đường trịn tâm I(a;b) bán kínhR 
 (x –a)2 + (y –b)2 = R2 
58) Phương trình đường trịn tâm I(a;b) bán kính R = , điều kiện 
59) Phương trình tiếp tuyến của đường trịn (C) tâm I(a;b). Gọi là tiếp tuyến với (C) tại M0 (C)
 (x0 –a)(x –x0) + (y0 –b)(y –y0) = 0 
60) Phương trình đường elip
 M(x;y)( E)
 Trong đĩ b2 = a2 –c2 
Quan hệ vuơng gĩc
61/ Chứng minh hai đường thẳng vuơng gĩc.
 C1 : Dùng các quan hệ vuơng gĩc đã biết trong mặt phẳng.
 C2 : gĩc.
P
 C3: Dùng hệ quả:
 C4: Dùng hệ quả:
// , 
 C5 : Dùng hệ quả:
 C6 : Sử dụng định lí ba đường vuơng gĩc.
 C7: Dùng hệ quả: Nếu một đường thẳng vuơng gĩc với hai cạnh của một tam giác thì vuơng gĩc với cạnh cịn lại của tam giác
62/ Chứng minh đường thẳng vuơng gĩc mặt phẳng.
 C1 : Dùng định lý: Đường thẳng vuơng gĩc với mặt phẳng khi nĩ vuơng gĩc với hai đường thẳng cắt nhau nằm trong mặt phẳng
, cắt nhau , , 
 C2 : Dùng hệ quả: Cho hai đường thẳng // nếu đường thẳng này vuơng gĩc với mặt phẳng thì đường thẳng kia cũng vuơng gĩc với mặt phẳng
// , 
 C3 : Dùng hệ quả: Cho hai mặt phẳng vuơng gĩc theo giao tuyến b, nếu đường thẳng a nằm trong mẵt phẳng này vuơng gĩc với giao tuyến b thì đường thẳng a cũng vuơng gĩc với mặt phẳng kia
 C4 : Dùng hệ quả: Nếu hai mặt phẳng cắt nhau cùng vuơng gĩc với mặt phẳng thứ ba thì giao tuyến của hai mặt phẳng này cũng vuơng gĩc với mặt phẳng thứ ba đĩ
63/ Chứng minh hai mặt phẳng vuơng gĩc .
O
 C1 : Chứng minh gĩc giữa chúng là một vuơng.
, , 
Khi đĩ:
 gĩc gĩc 
 C2 : Dùng hệ quả:Cho hai mặt phẳng vuơng gĩc với nhau nếu cĩ một đường thẳng nằm trong mặt phẳng này vuơng gĩc với mặt phẳng kia.
CÁCH XÁC ĐINH GĨC
64/ Gĩc của hai đường thẳng
Chọn điểm O tuỳ ý.
Dựng qua O : a’ // a; b’ // b .
Gĩc (a,b) = gĩc (a’,b’) =
Thường chọn điểm O a hoặc O b
65/ Gĩc của hai mặt phẳng
Chọn điểm O thuộc giao tuyến của và .
Dựng qua O : và 
Gĩc = Gĩc = 
Chú ý: * 
 * Nếu thi chọn gĩc 
6/ Gĩc của đường thẳng và mặt phẳng 
Gĩc giữa đường thẳng và mặt phẳng là gĩc giữa đường thẳng đĩ và hình chiếu của nĩ trên mặt phẳng
Chọn điểm A thuộc đường thẳng a.
Dựng qua tại B.
 Dựng giao điểm O của a và nếu chưa cĩ. 
 ( OB là hình chiếu của a trên mặt phẳng ())
Khi đĩ: Gĩc = Gĩc = .
KHOẢNG CÁCH
Khoảng cách từ một điểm
đến một mặt phẳng
Khoảng cách từ một điểm
đến một đường thẳng
Khoảng cách giữa hai đường thẳng song song
Khoảng cách giữa mặt phẳng và đường thẳng // song song
Khoảng cách giữa hai 
mặt phẳng song song
Khoảng cách giữa hai 
Đường thẳng chéo nhau
HÌNH VẼ MỘT SỐ HÌNH CHĨP ĐẶC BIỆT
67/ Hình chóp tam giác đều
	 Hình chĩp tam giác đều:
 Đáy là tam giác đều
 Các mặt bên là những tam giác cân
 Đặc biệt: Hình tứ diện đều cĩ:
 Đáy là tam giác đều
 Các mặt bên là những tam giác đều
 Cách vẽ: 
 Vẽ đáy ABC Vẽ trung tuyến AI
 Dựng trọng tâm H Vẽ SH (ABC)
 Ta cĩ: 
 SH là chiều cao của hình chĩp
 Gĩc giữa cạnh bên và mặt đáy là: .
 Gĩc mặt bên và mặt đáy là: 
68/ Hình chĩp tứ giác đều
	 Hình chĩp tứ giác đều:
 Đáy là hình vuơng
 Các mặt bên là những tam giác cân
 Cách vẽ: 
 Vẽ đáy ABCD 
 Dựng giao điểm H của hai đường chéo AC & BD 
 Vẽ SH (ABCD)
 Ta cĩ: 
 SH là chiều cao của hình chĩp
 Gĩc giữa cạnh bên và mặt đáy là: .
 Gĩc mặt bên và mặt đáy là: 
69/ Hình chĩp cĩ một cạnh bên vuơng gĩc với đáy
 SA (ABC) 
 Gĩc giữa cạnh bên SB và mặt đáy là: 
 Gĩc giữa cạnh bên SC và mặt đáy là: 
.
 SA (ABCD) 
 Gĩc giữa cạnh bên SB và mặt đáy là: 
 Gĩc giữa cạnh bên SC và mặt đáy là: 
 Gĩc giữa cạnh bên SD và mặt đáy là: 
70) Chú ý:
 a/ Đường chéo của hình vuơng cạnh a là d = a, 
 Đường chéo của hình lập phương cạnh a là d = a, 
 Đường chéo của hình hộp chữ nhật cĩ 3 kích thước a, b, c là d = ,
 b/ Đường cao của tam giác đều cạnh a là h = 
 c/ Hình chĩp đều là hình chĩp cĩ đáy là đa giác đều và các cạnh bên đều bằng 
nhau ( hoặc cĩ đáy là đa giác đều, hình chiếu của đỉnh trùng với tâm của đáy).
 d/ Lăng trụ đều là lăng trụ đứng cĩ đáy là đa giác đều.	
THỂ TÍCH KHỐI ĐA DIỆN
71) Thể tích khối lăng trụ
 Với: B là diện tích mặt đáy
 h là chiều cao
72) Thể tích khối hộp chữ nhật
 Với a, b, c là ba kích thước
73) Thể tích khối lập phương
 Với a là độ dài cạnh
74) Thể tích khối chĩp 
 B là diện tích mặt đáy
 h là chiều cao
75) Tỉ số thể tích tứ diện
 Cho khối tứ diện SABC và , , là các điểm tùy ý lần lượt thuộc SA, SB, SC ta cĩ
76) Thể tích khối chĩp cụt CDEC’D’E’: 
 B, B’ là diện tích hai đáy
 h là chiều cao