Ôn tập giải tích – Chương I

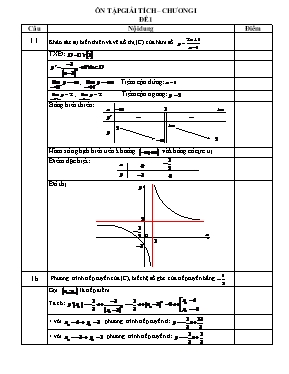
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 1
Câu
Nội dung
Điểm
1.1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
TXĐ: 
 ; Tiệm cận đứng: 
 ; Tiệm cận ngang: 
Bảng biến thiên:
Hàm số nghịch biến trên khoảng và không có cực trị
Điểm đặc biệt:
Đồ thị
o
1b
 Phương trình tiếp tuyến của (C), biết hệ số góc của tiếp tuyến bằng 
Gọi là tiếp điểm
Ta có: 
+ với . phương trình tiếp tuyến d: 
+ với . phương trình tiếp tuyến d: 
1c
Tìm để đường thẳng luôn cắt đồ thị (C) tại hai điểm phân biệt A, B sao cho AB ngắn nhất
Phương trình hoành độ giao điểm của d và đồ thị (C)
 điều kiện: 
 (1)
Ta có: 
 Phương trình (1) luôn có 2 nghiệm phân biệt
Do đó: đường thẳng d luôn cắt đồ thị (C) tại 2 điểm phân biệt A, B
Gọi là 2 nghiệm của phương trình (1), khi đó: 
 , 
 khi 
2.1
Tìm GTLN, GTNN của hàm số trên đoạn 
Trên đoạn , ta có: 
 , , , 
Vậy: , 
2.2
Tìm để hàm số có cực đại, cực tiểu
TXĐ: ; ; 
Hàm số có cực đại, cực tiểu khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt hoặc 
3
Tìm để phương trình: (1) có nghiệm.
Điều kiện: 
Đặt ; 
 ta có: 
 ; (có thể lập bảng biến thiên)
Do đó: 
Phương trình (1) thành: (2)
Đặt: 
Phương trình (2) có nghiệm khi và chỉ khi d và (C) có điểm chung
 với 
 ; 
Bảng biến thiên: 
4 
Phương trình (1) có nghiệm 
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 2
Câu
Nội dung
Điểm
1.1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
TXĐ: 
 ; 
 ; 
Bảng biến thiên:
Hàm số đồng biến trên các khoảng và 
Nghịch biến trên khoảng 
Đạt cực đại tại và , Đạt cực tiểu tại và 
Điểm đặc biệt:
Đồ thị
o
1.2
Viết phương trình tiếp tuyến d của đồ thị (C) tại điểm có hoành độ 
Gọi là tiếp điểm
 Phương trình tiếp tuyến d: 
1.3
Tìm để phương trình có ba nghiệm phân biệt.
Đặt: 
Số nghiệm của phương trình (1) là số giao điểm của d và (C)
Phương trình (1) có 3 nghiệm phân biệt 
2.1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 
Điều kiện: 
Trên đoạn ta có: 
Trên khoảng ta có: 
 ; 
Vậy: , 
2.2
Chứng minh rằng : đường thẳng luôn cắt đồ thị (C) tại hai điểm phân biệt A, B.Tìm để 
Phương trình hoành độ giao điểm của d và đồ thị (C)
 điều kiện: 
 (1)
Ta có: 
 Phương trình (1) luôn có 2 nghiệm phân biệt
Do đó: đường thẳng d luôn cắt đồ thị (C) tại 2 điểm phân biệt A, B
Gọi là 2 nghiệm của phương trình (1), khi đó: 
 , 
3.1
Cho hàm số (1). 
Tìm để hàm số (1) đồng biến trên tập xác định.
TXĐ: ; 
Hàm số (1) đồng biến trên khi va chỉ khi 
3.2
Tìm để hàm số (1) có cực đại, cực tiểu
 (2). Hàm số (1) có cực đại, cực tiểu khi và chỉ khi phương trình (2) có 2 nghiệm phân biệt 
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 3
Câu
Nội dung
Điểm
1.1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
TXĐ: 
 ; 
 ; 
Bảng biến thiên:
Hàm số đồng biến trên khoảng 
Nghịch biến trên các khoảng và 
Đạt cực đại tại và , Đạt cực tiểu tại và 
Điểm đặc biệt:
Đồ thị
o
1.2
Viết phương trình tiếp tuyến của (C), biết hệ số góc của tiếp tuyến bằng 
Gọi là tiếp điểm
Ta có: 
+ với . phương trình tiếp tuyến d: 
+ với . phương trình tiếp tuyến d: 
1.3
Tìm để phương trình có ba nghiệm phân biệt.
 (1)
Đặt: 
Số nghiệm của phương trình (1) là số giao điểm của d và (C)
Phương trình (1) có 3 nghiệm phân biệt 
2.1
Tìm để hàm số đạt cực tiểu tại 
TXĐ: ; ; 
 Hàm số đạt cực tiểu tại ,ta có: 
Khi ta có: hàm số đạt cực tiểu tại 
Vậy là giá trị cần tìm.
2.2
Tìm GTLN, GTNN của hàm số: trên đoạn 
Trên đoạn ta có: 
Trên khoảng ta có: 
 ; Vậy: ,
3
Tìm để phương trình: (1) có nghiệm.
Điều kiện: 
Đặt ; 
 ta có: 
 ; (có thể lập bảng biến thiên)
Do đó: 
Phương trình (1) thành: (2)
Đặt: 
Phương trình (2) có nghiệm khi và chỉ khi d và (C) có điểm chung
 với 
 ; 
Bảng biến thiên: 
4 
Phương trình (1) có nghiệm 
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 4
Câu
Nội dung
Điểm
1.1
Khảo sát và vẽ đồ thị (C) của hàm số khi 
khi hàm số thành: 
TXĐ: 
 ; 
 ; 
Bảng biến thiên:
Hàm số đồng biến trên các khoảng và 
Nghịch biến trên các khoảng và 
Đạt cực đại các tại , và 
 Đạt cực tiểu tại và 
Điểm đặc biệt:
Đồ thị
o
1.2
Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ 
Gọi là tiếp điểm
 Phương trình tiếp tuyến d: 
1.3
Tìm để hàm số (1) có 3 cực trị
 ; 
Hàm số (1) có 3 cực trị khi và chỉ khi phương trình có 3 nghiệm phân biệt phương trình có 2 nghiệm phân biệt khác 0 
2.1
Tìm để hàm số đạt cực đại tại 
TXĐ: ; 
 Hàm số đạt cực đại tại ,ta có: 
Khi ta có: ; 
Bảng biến thiên: 
Vậy là giá trị cần tìm.
2.2
Tìm GTLN, GTNN của hàm số: 
Điều kiện: 
Trên đoạn ta có: 
Trên khoảng ta có: 
 ; ; 
Vậy: , 
3
Cho hàm số: (C). Tìm để đường thẳng d: cắt đồ thị (C) tại 2 điểm phân biệt A;B sao cho diện tích OAB bằng (với O là gốc tọa độ)
Phương trình hoành độ giao điểm của d và đồ thị (C)
 điều kiện: 
 (1)
Ta có: 
 Phương trình (1) luôn có 2 nghiệm phân biệt
Do đó: đường thẳng d luôn cắt đồ thị (C) tại 2 điểm phân biệt A, B
Gọi là 2 nghiệm của phương trình (1), khi đó: 
 , 
 d: đi qua 2 điểm A,B 
Diện tích tam giác OAB: 
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 5
Câu
Nội dung
Điểm
1.1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
TXĐ: 
 ; 
 ; 
Bảng biến thiên:
Hàm số đồng biến trên các khoảng và 
Nghịch biến trên khoảng 
Đạt cực đại tại và , Đạt cực tiểu tại và 
Điểm đặc biệt:
Đồ thị
o
1.2
Viết phương trình tiếp tuyến d của đồ thị (C) tại điểm có hoành độ 
Gọi là tiếp điểm
 Phương trình tiếp tuyến d: 
1.3
Tìm để phương trình có ba nghiệm phân biệt.
Đặt: 
Số nghiệm của phương trình (1) là số giao điểm của d và (C)
Phương trình (1) có 3 nghiệm phân biệt 
2
Cho hàm số . Tìm để hàm số đạt cực đại, cực tiều lần lượt tại và sao cho 
TXĐ: 	 
Hàm số (1) có cực đại, cực tiểu khi và chỉ khi phương trình (2) luôn có 2 nghiệm phân biệt
Hai nghiệm của phương trình (2): 
Bảng biến thiên: 
Ta có: và ; 
 (3)
Ta xét 2 trường hợp:
 Phương trình (3) thành:
 (loại) 
 Phương trình (3) thành
\ Vậy: là giá trị cần tìm
3
Cho hàm số: (C). Tìm các giá trị của để đường thẳng d: cắt đồ thị (C) tại 2 điểm phân biệt A;B và đoạn thẳng AB ngắn nhất.
Phương trình hoành độ giao điểm của d và đồ thị (C)
 điều kiện: 
 (1)
Ta có: 
đường thẳng d cắt đồ thị (C) tại 2 điểm phân biệt A, B
 Phương trình (1) luôn có 2 nghiệm phân biệt
Gọi là 2 nghiệm của phương trình (1), khi đó: 
 , 
Áp dụng bất đẳng thức Cô-si với 2 số dương: và 
Dấu = xảy ra khi: 
Vậy khi thì 
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 6
Câu
Nội dung
Điểm
1.1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
TXĐ: 
 ; 
 ; 
Bảng biến thiên:
Hàm số đồng biến trên các khoảng và 
Nghịch biến trên khoảng 
Đạt cực đại tại và , Đạt cực tiểu tại và 
Điểm đặc biệt:
Đồ thị
o
1.2
Viết phương trình tiếp tuyến d của đồ thị (C) biết tọa độ tiếp điểm 
Gọi là tiếp điểm
 Phương trình tiếp tuyến d: 
1.3
Biện luận theo số nghiệm của phương trình 
Đặt: 
Số nghiệm của phương trình (1) là số giao điểm của d và (C)
Biện luận:
Số giao điểm của d và (C)
Số nghiệm của phương trình (1)
1
1
2
2
3
3
2
2
1
1
2
Cho hàm số. Tìm để hàm số đạt cực đại, cực tiều lần lượt tại và sao cho 
TXĐ: 	 
Hàm số (1) có cực đại, cực tiểu khi và chỉ khi phương trình (2) luôn có 2 nghiệm phân biệt
Hai nghiệm của phương trình (2): 
Bảng biến thiên: 
Ta có: và ; (3)
Ta xét 2 trường hợp:
Phương trình (3) thành:
 (loại)
Phương trình (3) thành:
Vậy: là giá trị cần tìm
3
Cho hàm số: (C). Tìm các giá trị của để đường thẳng d: cắt đồ thị (C) tại 2 điểm phân biệt A;B và đoạn thẳng AB ngắn nhất.
Phương trình hoành độ giao điểm của d và đồ thị (C)
 điều kiện: 
 (1)
Ta có: 
đường thẳng d cắt đồ thị (C) tại 2 điểm phân biệt A, B
 Phương trình (1) luôn có 2 nghiệm phân biệt
Gọi là 2 nghiệm của phương trình (1), khi đó: 
 , 
Áp dụng bất đẳng thức Cô-si với 2 số dương: và vơi 
Dấu = xảy ra khi: 
Vậy khi thì 
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 7
Câu
Nội dung
Điểm
1.1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
TXĐ: 
 ; Tiệm cận đứng: 
 ; Tiệm cận ngang: 
Bảng biến thiên:
Hàm số nghịch biến trên khoảng và không có cực trị
Điểm đặc biệt:
Đồ thị
o
1.2
 Phương trình tiếp tuyến của (C), biết hệ số góc của tiếp tuyến bằng 
Gọi là tiếp điểm
Ta có: 
+ với . phương trình tiếp tuyến d: 
+ với . phương trình tiếp tuyến d: 
1.3
Tìm trên đồ thị (C) các điểm có tọa độ nguyên.
Các điểm thuộc (C) có tọa độ nguyên: 
1.4
Chứng minh rằng: đường thẳng d: luôn cắt đồ thị (C) tại hai điểm phân biệt A, B. Tìm để tam giác OAB có diện tích bằng 4 ( O là gốc tọa độ)
Phương trình hoành độ giao điểm của d và đồ thị (C)
 điều kiện: 
 (1)
Ta có: 
 Phương trình (1) luôn có 2 nghiệm phân biệt
Do đó: đường thẳng d luôn cắt đồ thị (C) tại 2 điểm phân biệt A, B
Gọi là 2 nghiệm của phương trình (1), khi đó: 
 , 
 d: đi qua 2 điểm A,B 
Diện tích tam giác OAB: 
Vậy: và là giá trị cần tìm
2.1
Cho hàm số. Tìm để hàm số đạt cực đại, cực tiểu tại thỏa mãn 
TXĐ: 	
 (2)
Hàm số (1) có cực đại, cực tiểu khi và chỉ khi phương trình (2) luôn có 2 nghiệm phân biệt
 hoặc 
Gọi là hai nghiệm của (2), ta có: ; 
Ta có: 
3
Tìm để bất phương trình nghiệm đúng 
 (1)
Đặt: với 
Bảng biến thiên: 
Ta có: ; 
 ; 
Từ (1), ta có: 
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 8
Câu
Nội dung
Điểm
1.1
Khảo sát và vẽ đồ thị của hàm số. (C)
TXĐ: 
 ; 
Bảng biến thiên:
Hàm số đồng biến trên các khoảng và 
Nghịch biến trên các khoảng và 
Đạt cực đại tại và 
Đạt cực tiểu các tại , và 
Điểm đặc biệt:
Đồ thị
o
1.2
Viết phương trình tiếp tuyến của (C) tại điểm thuộc (C), 
biết và 
 + 
Phương trình tiếp tuyến d: 
1.3
Dựa vào đồ thị (C), tìm để phương trình có 4 nghiệm phân biệt .
 (1)
Đặt: 
Số nghiệm của phương trình (1) là số giao điểm của d và (C)
Phương trình (1) có 4 nghiệm phân biệt 
2
Cho hàm số: (C). Tìm để đường thẳng d: cắt đồ thị (C) tại 2 điểm phân biệt A;B và AB
Phương trình hoành độ giao điểm của d và đồ thị (C)
 điều kiện: 
 (1)
Ta có: 
đường thẳng d cắt (C) tại 2 điểm phân biệt A, B
Gọi là 2 nghiệm của phương trình (1), khi đó: 
 , 
AB
 (thỏa)
3
Cho hàm số . Tìm để hàm số đạt cực đại, cực tiểu tại thỏa mãn 
TXĐ: 	
 (2)
Hàm số (1) có cực đại, cực tiểu khi và chỉ khi phương trình (2) luôn có 2 nghiệm phân biệt
Gọi là hai nghiệm của (2), ta có: ; 
Giải hệ: 
Giải (3): (thỏa)
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 9
Câu
Nội dung
Điểm
1.1
Khảo sát và vẽ đồ thị của hàm số. (C)
TXĐ: 
 ; Tiệm cận đứng: 
 ; Tiệm cận ngang: 
Bảng biến thiên:
Hàm số đồng biến trên khoảng và 
Hàm số không có cực trị
Điểm đặc biệt:
Đồ thị
o
2
Viết phương trình tiếp tuyến của (C) tại điểm có tung độ 
 3. Phương trình tiếp tuyến d: 
3
Tìm tọa độ điểm M thuộc đồ thị (C) sao cho khoảng cách từ điểm M đến đường thẳng là nhỏ nhất.
Đồ thị
o
Nhận xét: để khoảng cách tử điểm đến đường thẳng d nhỏ nhất, ta chọn nhánh bên phải của tiệm cận đứng: 
 với 
Xét hàm số: với 
 ; 
Bảng biến thiên:
 khi 
 khi ; 
Vậy khi ( quan sát đồ thị)
2
Cho hàm số . Tìm để hàm số đạt cực đại, cực tiểu tại thỏa mãn 
TXĐ: 	 ; 
Hàm số (1) có cực đại, cực tiểu khi và chỉ khi phương trình (2) luôn có 2 nghiệm phân biệt 
 hoặc 
Giải hệ: 
3
Tìm để hàm số nghịch biến trên đoạn có độ dài bằng 1
TXĐ: 	 
 (2) 
Ta có: , Ta xét các trường hợp sau:
Khi đó: Hàm số (1) đồng biến trên (không thỏa)
Phương trình (2) có 2 nghiệm 
Vì hàm số nghịch biến trong khoảng 
Ta có: ; 
Theo đề bài ta có: 
ÔN TẬP GIẢI TÍCH – CHƯƠNG I
ĐỀ 10
Câu
Nội dung
Điểm
1.1
Khảo sát và vẽ đồ thị của hàm số. (C)
TXĐ: 
 ; Tiệm cận đứng: 
 ; Tiệm cận ngang: 
Bảng biến thiên:
Hàm số đồng biến trên các khoảng và 
Hàm số không có cực trị
Điểm đặc biệt:
Đồ thị
o
2
Viết phương trình tiếp tuyến của (C), biết tiếp tuyến song song với đường thẳng 
 hệ số góc của đường thẳng 
Gọi là hệ số cóc của tiếp tuyến d
Gọi là tiếp điểm
Ta có: 
+ với . phương trình tiếp tuyến d: 
+ với . phương trình tiếp tuyến d: 
3
Tìm tọa độ điểm M thuộc (C), biết tiếp tuyến của (C) tại điểm M cắt hai trục tọa độ tại A và B sao cho tam giác OAB có diện tích bằng 
Phương trình tiếp tuyến d của (C) tại điểm M
. Tọa độ điểm A là nghiệm của hệ:
. Tọa độ điểm B là nghiệm của hệ:
Diện tích tam giác OAB: 
 với 
Với ; Với 
2
Cho hàm số: (C). Tìm tọa độ điểm M thuộc (C) sao cho khoảng cách từ điểm M đến đường thẳng bằng 
 ; 
 với 
Với ; Với 
3.1
Tìm để hàm số (1) đồng biến trên đoạn có độ dài bằng 2
 TXĐ: 	 
 (2) 
Ta có: , Ta xét các trường hợp sau:
Khi đó: Hàm số (1) nghịch biến trên (không thỏa)
Phương trình (2) có 2 nghiệm 
Vì hàm số đồng biến trong khoảng 
Ta có: ; 
Theo đề bài ta có: 
3.2
Cho hàm số (1). Tìm để hàm số đạt cực đại, cực tiểu tại thỏa mãn 
TXĐ: 	 
 (2) 
Hàm số (1) có cực đại, cực tiểu khi và chỉ khi phương trình (2) luôn có 2 nghiệm phân biệt
 hoặc 
Gọi là hai nghiệm của (2), ta có: ; 
Giải hệ: 
Giải (3):