Kiểm tra học kỳ I môn Toán học 9

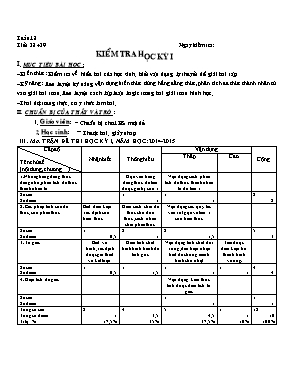
Tuần 18	 
Tiết 38 +39 Ngày kiểm tra:
 KIỂM TRA HỌC KỲ I
I. MỤC TIÊU BÀI HỌC :	
-Kiến thức: Kiểm tra về hiểu bài của học sinh, biết vận dụng lý thuyết để giải bài tập 
-Kỹ năng: Rèn luyện kỹ năng vận dụng kiến thức dùng hằng đẳng thức, phân tích đa thức thành nhân tử
vào giải bài toán.Rèn luyện cách lập luận lo gic trong bài giải toán hình học. 
-Thái độ:trung thực, có ý thức làm bài. 
II. CHUẨN BỊ CỦA THẦY VÀ TRÒ :
1. Giáo viên : - Chuẩn bị cho 1HS một đề
 2. Học sinh : - Thuộc bài, giấy nháp 
 III . MA TRẬN ĐỀ THI HỌC KỲ I, NĂM HỌC: 2014-2015
 Cấp độ
Tên chủ đề
(nội dung, chương)
Nhận biết
Thơng hiểu
Vận dụng
Cộng
Thấp
Cao
1.Những hằng đẳng thức đáng nhớ, phân tích đa thức thành nhân tử
Dựa vào hằng đẳng thức để tìm được giá trị của x
Vận dụng cách phân tích đa thức thành nhân tử để tìm x
Số câu
Số điểm
1
1
1
1
2
2
2. Các phép tính của đa thức, của phân thức
Biết điều kiện xác định của biểu thức 
Hiểu cách chia đa thức cho đơn thức ,cách nhân chia phân thức
Vận dụng các quy tắc vào rút gọn và tìm x của biều thức
Số câu
Số điểm
1
0,5
2
1
2
1,5
5
3
3. Tứ giác
Biết vẽ hình,xác định được giả thiết và kết luận
Hiểu tính chất hình bình hành để tính gĩc
Vận dụng tính chất đối xứng, dấu hiệu nhận biết để chứng minh hình chữ nhật 
Tìm được điều kiện trở thành hình vuơng.
Số câu
Số điểm
1
0,5
1
1,5
1
1
1
1
4
4
4. Diện tích đa giác
Vận dụng kiến thức tính được diên tích tứ giác
Số câu
Số điểm
1
1
1
1
Tổng số câu 
Tổng số điểm
Tỉ lệ: %
2
1
17,5%
4
3,5
35%
5
4,5
37,5%
1
1
10%
12
10
100%
PHỊNG GD & ĐT MANG YANG ĐỀ KIỂM TRA HỌC KÌ I – NĂM HỌC 2014 -2015
 Trường THCS Ayun Mơn: Tốn Lớp 8 
Lớp: Thời gian: 90 phút
Họ và tên: (Khơng kể thời gian phát đề) 
ĐỀ BÀI:
 Bài 1: (1 điểm): Tính 
(24x5 -20x4) : 4x4
 Bài 2 / (2 điểm ) : Tìm x , biết :
 a/ x2 + 6x + 9 = 0 
 b/ 3 (3x - 2) + 3x2 - 2x = 0 
 Bài 3: (2 điểm): Cho biểu thức : A = .
a) Tìm điều kiện của x để giá trị của A xác định .
b) Rút gọn biểu thức A .
c) Tìm giá trị của x để giá trị của A bằng 1 .
 Bài 4: (1,5 điểm):
 Cho hình bình hành ABCD ,biết . Tính, , và 
Bài 5 / (3,5 điểm ) : Cho tam giác HIK cân tại H , đường trung tuyến HM . Gọi N là trung điểm của HK và E là điểm đối xứng với M qua N .
a) Tứ giác HMKE là hình gì ? Vì sao ?
b) Cho HK = 5 cm ; IK = 8 cm . Tính diện tích tứ giác HMKE.
c) Tìm điều kiện của tam giác HIK để tứ giác HMKE là hình vuông .
ĐÁP ÁN VÀ THANG ĐIỂM KIỂM TRA HỌC KÌ I – NĂM HỌC 2014 - 2015
Mơn: Tốn Lớp 8 
Bài 1
( 1 ,0đ)
a) (24x5 –20x4) : 4x4 = 6x – 5
0,5
b) = 
0,5
Bài 2
(2,0đ)
a) x2 + 6x + 9 = 0 ( x + 3)2 = 0
 x + 3 = 0
 x = – 3 
0,5
0,25
0,25
 b/ 3 (3x –2) + 3x2 – 2x = 0 
 3 (3x – 2) + x (3x – 2) = 0 
 (3x – 2) (3 + x) = 0 
 3x – 2 = 0 hoặc 3 + x = 0
 x = 2/3 hoặc x = – 3
0,25
0,25
0,25
0,25
Bài 3
(2đ)
Để biểu thức A có giá trị xác định thì 
 ( x + 1) ( 2x – 8 ) 0 
 x + 1 0 và 2x – 8 0 x -1 và x 4 
0,5
 b) A = 
0,7 5
 c) Ta có : Giá trị của biểu thức B bằng 1 khi 
 3x = 2x -8 
 x = -8 ( Thoả mãn điều kiện xác định ) . 
Vậy khi giá trị của x = -8 thì giá trị của biểu thức A bằng 1. 
0,25
0,25
0,25
Bài 4
(1,5 đ)
Xét hình bình hành ABCD; 
Vì AB//CD (cạnh đối hình bình hành)
 nên ( cặp gĩc trong cùng phía) 
 => = 1800-1100=700 
 Vì = , = ( gĩc đối hình bình hành)
= 1100 ; = 700
0,25
0,5
0,25
0,5
Bài 5
(3,5 đ)
vẽ hình đúng ; ghi giả thiết và kết luận đúng 
GT: HIK ( HI = HK ) ;
 HN = NK ( NHK) ; KM = MI ( MIK) ; 
 E đối xứng với M qua N 
 HK = 5 cm ; IK = 8 cm
KL : a) Tứ giác HMK E là hình gì ? Vì sao ? 
 b) Tính S HMKE .
 c) Tìm điều kiện của tam giác HIK để tứ giác HMKE là hình vuông .
Chứng minh 
a) Xét tứ giác HMKE có HN = NK ( gt ) ; NM = NE ( Vì E là điểm đối xứng với M qua N ), suy ra tứ giác HMKE là hình bình hành . (1) 
Mặt khác:Tam giác HIK cân tại H mà HM là đường trung tuyến nên HM cũng là đường cao,suy ra = 900 (2) 
Từ (1) và (2) suy ra tứ giác HMKE là hình chữ nhật . 
0,5
0,5
0,5
b/Ta có MK = mà IK = 8 cm nên MK = 4cm .
Xét tam giác M HK vuông tại M có HM =( Theo định lí Py ta go) . Suy ra HM = = = 3 (cm) 
Vậy SHMKE = M H . MK = 3 . 4 = 12 ( cm2 ) .	( 1điểm ) 
0,25
0,25
0,5
c) Để hình chữ nhật HMKE là hình vuông thì M H = MK mà MK = IK 
 nên M H = IK .
Xét tam giác HIK có M H = IK và HK = HI, suy ra HIK là tam giác vuông cân . 
0,5
0,5
Lưu ý :Mọi cách giải đúng đều đạt điểm tối đa