Kieåm tra giữa kì I môn Toán- Lớp 11

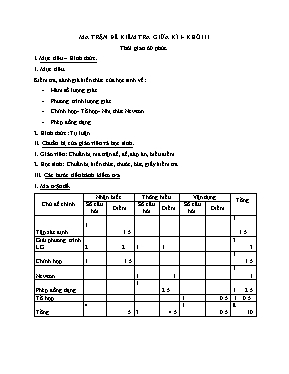
MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ I- KHỐI 11
Thời gian 60 phút.
I. Mục tiêu – Hình thức.
1. Mục tiêu.
Kiểm tra, đánh giá kiến thức của học sinh về: 
Hàm số lượng giác
Phương trình lượng giác
Chỉnh hợp- Tổ hợp- Nhị thức Newton
Phép đồng dạng
2. Hình thức: Tự luận.
II. Chuẩn bị của giáo viên và học sinh.
1. Giáo viên: Chuẩn bị ma trận đề, đề, đáp án, biểu điểm.
2. Học sinh: Chuẩn bị kiến thức, thước, bút, giấy kiểm tra ...
III. Các bước tiến hành kiểm tra.
1. Ma trận đề. 
Chủ đề chính
Nhận biết
Thông hiểu
Vận dụng
Tổng
Số câu hỏi
Điểm
Số câu hỏi
Điểm
Số câu hỏi
Điểm
Tập xác định
1
 1.5
1
 1.5
Giải phương trình LG
2
 2 
1
 1
3
3
Chỉnh hợp
1
1.5
1
 1.5
Newton
1
1
1
 1
Phép đồng dạng
1
2.5
1 2.5 
Tổ hợp
1
0.5
 1 0.5 
Tổng
4
5
3
4.5
1
0.5
8
10
 SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỒNG NAI	 KIEÅM TRA GIỮA KÌ I
 TRƯỜNG THPT NGUYỄN VĂN TRỖI Môn :Toán- Lớp 11 
 TỔ TOÁN-TIN 	 Thời gian: 60 phút
	 Không kể thời gian giao đề
	ĐỀ BÀI 	
	Bài 1(1.5đ): Tìm tập xác định của hàm số sau : 
 fx=sinx+ cos3x1-sinx
 Bài 2(3đ): Giải phương trình sau:
tanx+π6-3 = 0 b) sin2x-4 = 4cosx-2sinx 
 c) 2cos2x+3sinx+5=0 
 Bài 3(2.5đ): a) Từ các chữ số 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có năm chữ số khác nhau và chia hết cho 2 ?
 b) Tìm hệ số của x2015 trong khai triển 3+x52016
 Bài 4( 2.5đ): Cho (C) : x2 + y2 -4x +6y - 3 = 0. Tìm ảnh của (C) qua phép đồng dạng bằng cách thực liên tiếp phép tiến v=(-2; 3) và phép vị tự tâm O tỉ số bằng 2
 Bài 5 ( 0.5đ): Trong một đa giác lồi 2015 cạnh, ta kẻ tất cả các đường chéo. Biết rằng không có ba đường chéo nào trong chúng đồng quy. Tìm số giao điểm của các đường chéo này.
 ĐÁP ÁN CHẤM BÀI GIỮA KÌ I- TOÁN KHỐI 11
Câu1 (1.5 đ) 
 fx=sinx+ cos3x1-sinx
 Hàm số xác định khi 1 - sinx ≠0
 ó sinx ≠ 1 ó x ≠π2+k2π , k∈Z
1,0 đ
 Vậy D= R\ π2+k2π, k∈Z
0,5 đ
Câu 2: ( 3 đ) 
tanx+π6-3 = 0 ó tanx+π6=3=tanπ3
0,5 đ
 ó x+π6= π3+kπ , k∈Z
0,25 đ
 ó x = π6+ kπ , k∈ Z
 Vậy phương trình có nghiệm x = π6+ kπ , k∈ Z
0,25 đ
sin2x-4 = 4cosx-2sinx ó 2sinxcosx – 4 -4 cosx + 2sinx = 0
 ó 2sinx( cosx + 1) – 4(cosx + 1) = 0
 ó ( 2sinx – 4) ( cosx +1 ) = 0 
0.5đ
 ó 2sinx-4=0cosx+1=0 ó x= π+k2π ¸ k∈Z
 0.5 đ
 2cos2x+3sinx+5=0 
ó 2( 1-2sin2x)+3sinx+5=0
ó -4sin2x+3sinx+7=0
 0.5 đ
 ó sinx=-1sinx=74( loại) ó x = -π 2+ k2π , k∈Z
 0.5 đ
Câu 3: (2.5đ): a) Gọi chữ số cần tìm là: a1a2a3a4a5
0.25 đ
 Vì số đó chia hết cho 2 nên: a5 ∈2;4;6 do đó a5 có 3 cách chọn
 4 chữ số còn lại được lấy từ 6 chữ số còn lại khác nhau là một chỉnh hợp chập 4 của 6 phần tử là A46 = 360 ( số).
0,75 đ
0,25đ
 Vậy số cần tìm là 3.360 = 1008 số
0,25 đ
Tìm hệ số của x2015 trong khai triển 3+x52016
 Ta có 3+x52016 có số hạng tổng quát là: C2016k32016-kx5k
0,25 đ
 = C2016k32016-kx5k
0,25 đ
 Hệ số của x2015 ứng với 5k = 2015 ó k = 403
0,25 đ
 Vậy hệ số cần tìm là C201640331613 
 0.25 đ
Câu 4: ( 2.5 đ) 
 (C) có tọa độ tâm I( 2; -3) và bán kính R = 4
0.25 đ
Phép tịnh tiến: Gọi (C’) = Tv (C) nên (C’) có tọa độ tâm O (0; 0) và bán kính R= 4
 0.75 đ
 (C’) là x2+y2=16
 0.25 đ
 Phép vị tự: Gọi (C’’) = VO;2(C') nên 
 (C’’) có tọa độ tâm O( 0; 0) và bán kính R’’= 8
0,25 đ
0.75đ
 (C’’) là x2+y2=64
0,25 đ
Câu 5: (0,5đ) 
Mỗi giao điểm của hai đường chéo ứng với một và chỉ một bộ là 4 đỉnh của đa giác
Nên số giao điểm cần tìm là C42015
 0.5 đ