Đề thi thử học kì I Toán lớp 12 - Đặng Việt Hùng

Khóa học LUYỆN ĐỀ TRẮC NGHIỆM TOÁN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 
Chương trình Luyện thi new PRO–S Toán 2017: Giải pháp tối ưu nhất cho kì thi THPT Quốc Gia 2017! 
VIDEO BÀI GIẢNG và LỜI GIẢI CHI TIẾT CÁC BÀI TẬP chỉ có tại website MOON.VN 
Group thảo luận bài tập : https://www.facebook.com/groups/Thayhungdz 
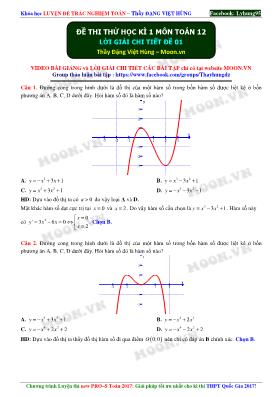
Câu 1. Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn 
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? 
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
A. 3 3 1y x x= − + + B. 3 23 1y x x= − + 
C. 3 23 1y x x= + + D. 3 23 1y x x= − − − 
HD: Dựa vào đồ thị ta có 0a > do vậy loại A và D. 
Mặt khác hàm số đạt cực trị tại 0x = và 2x = . Do vậy hàm số cần chọn là 3 23 1y x x= − + . Hàm số này 
có 2
0
' 3 6 0
2
x
y x x
x
=
= − = ⇔ 
=
. Chọn B. 
Câu 2. Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn 
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? 
-2 -1 1 2
-2
-1
1
2
x
y
A. 3 23 1y x x= − + + B. 4 22y x x= − + 
C. 4 22 2y x x= − + + D. 4 22 2y x x= − − + 
HD: Dựa vào đồ thị ta thấy đồ thị hàm số đi qua điểm ( )0;0O nên chỉ có đáp án B chính xác. Chọn B. 
ĐỀ THI THỬ HỌC KÌ 1 MÔN TOÁN 12 
LỜI GIẢI CHI TIẾT ĐỀ 01 

	

	
Khóa học LUYỆN ĐỀ TRẮC NGHIỆM TOÁN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 
Chương trình Luyện thi new PRO–S Toán 2017: Giải pháp tối ưu nhất cho kì thi THPT Quốc Gia 2017! 
Câu 3. Cho hàm số ( )y f x= xác định, liên tục trên R và có bảng biến thiên : 
x -∞ 2− 0 +∞ 
y’ - || + 0 + 
y 
+∞ + ∞ 
 4− 
Khẳng định nào sau đây là khẳng định đúng ? 
A. Hàm số có đúng hai cực trị. B. Hàm số có giá trị nhỏ nhất bằng 4− . 
C. Hàm số có giá trị cực tiểu bằng 0. D. Hàm số không xác định tại 2x = − . 
HD: Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại 2x = − . Tuy rằng hàm số không có đạo hàm 
tại điểm 2x = − nhưng vẫn đạt cực trị tại điểm 2x = − là điểm cực trị duy nhất và giá trị của cực tiểu là 
4y = − . Hàm số đạt giá trị nhỏ nhất tại 2x = − và min 4
x R
y
∈
= − . Chọn B. 
Câu 4. Cho hàm số ( )y f x= có 
( 1)
lim ( )
x
f x
+→ −
= +∞ và 
1
lim ( )
x
f x
−→
= +∞ . Chọn mệnh đề đúng ? 
A. Đồ thị hàm số đã cho không có tiệm cận đứng. 
B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng. 
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y = 1 và y = −1. 
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 1 và x = −1. 
HD: Ta có 
( 1)
lim ( )
x
f x
+→ −
= +∞ và 
1
lim ( )
x
f x
−→
= +∞ nên đồ thị hàm số đã cho có 2 đường tiệm cận đứng là 
1x = và 1x = − . Chọn D. 
Câu 5. Tìm giá trị cực đại 
ĐCy của hàm số
3 3 4y x x+= − − . 
A. 1CĐy = − . B. 7CĐy = − . C. 4CĐy = − . D. 2CĐy = − . 
HD: Ta có: 2' 3 3 0 1y x x= − + = ⇔ = ± . Do hàm số có 1a = − nên 1 2CD CT CD CDx x x y> ⇒ = ⇒ = − . 
Chọn D. 
Câu 6. Tìm khoảng đồng biến của hàm số 3 3 4y x x= − + − . 
A. ( ) ( ) ; 1 1;và−∞ − +∞ . B. ( )0;2 . C. ( )1;1− . D. ( )0;1 . 
HD: Ta có: 2 2' 3 3 0 1 0 1 1y x x x= − + > ⇔ − < ⇔ − < < do vậy hàm số đồng biến trên khoảng ( )1;1− . 
Chọn C. 
Câu 7. Đường thẳng 3y x= − cắt đồ thị hàm số 3 22 2y x x−= − tại điểm có tọa độ 0 0( ; )x y . Tìm 0y ? 
A. 0 0y = . B. 0 1y = . C. 0 3y = − . D. 0 2y = − . 
HD: PT hoành độ giao điểm của 2 đồ thị là: 3 2 3 22 2 3 2 3 2 0x x x x x x− − = − ⇔ − + − = 
0 0 01 1 3 3x x y x⇔ = ⇒ = ⇒ = − = − . Chọn C. 
Câu 8. Tìm giá trị nhỏ nhất của hàm số 2x 2 xy e e= + trên đoạn [ ]0;2 . 
A. [ ]0;2min 3.y = B. [ ]
4 2
0;2
min 2 2 .y e e= + 
Khóa học LUYỆN ĐỀ TRẮC NGHIỆM TOÁN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 
Chương trình Luyện thi new PRO–S Toán 2017: Giải pháp tối ưu nhất cho kì thi THPT Quốc Gia 2017! 
C. [ ]
4 2
0;2
min 2 .y e e= + D. [ ] 20;2
1 2
min .y
e e
= + 
HD: Ta có: ( ) [ ]( )2' 2 2 2 1 0 0;2x x x xy e e e e x= + = + > ∀ ∈ . Do đó hàm số đã cho liên tục và đồng biến 
trên đoạn [ ]0;2 do vậy GTNN của hàm số đã cho trên đoạn [ ]0;2 là ( ) 0 00 2 3y e e= + = . Chọn A. 
Câu 9. Tìm giá trị nhỏ nhất của hàm số 3
1
xy
x
+
=
−
 trên đoạn [ ]1;0− . 
A. [ ]1;0min 3.y− = − B. [ ]1;0min 2.y− = − C. [ ]1;0min 4.y− = − D. [ ]1;0min 3.y− = 
HD: Ta có: ( )2
4
' 0
1
y
x
−
= <
−
 nên hàm số đã cho liên tục và nghịch biến trên đoạn [ ]1;0− do đó GTNN 
của hàm số đã cho trên trên đoạn [ ]1;0− là ( )0 3y = − . Chọn A. 
Câu 10. Tìm giá trị lớn nhất của hàm số 2x 2 2xy e e= − + trên đoạn [ ]1;2− . 
A. [ ]
4 2
1;2
max 2 2.y e e
−
= − + B. [ ]
4 2
1;2
max 2 2 .y e e
−
= − 
C. [ ]
4 2
1;2
max 2 2.y e e
−
= − + D. [ ]
4 2
1;2
max 2 2 2.y e e
−
= − + 
HD: Ta có: ( )2' 2 2 0 2 1 0 0x x x xy e e e e x= − = ⇔ − = ⇔ = . Do hàm số liên tục trên đoạn [ ]1;2− 
Lại có ( ) ( ) ( ) 4 221 21 2; 0 1; 2 2 2y y y e ee e− = − + = = − + . Dựa vào đó suy ra GTLN của hàm số đã cho trên 
đoạn [ ]1;2− là 4 22 2e e− + . Chọn A. 
Câu 11. Tìm tất cả các giá trị của tham số m để hàm số 3 2 23( 1) 3 4 1y x m x m x m= − + − − − + nghịch biến 
trên tập xác định của nó. 
A. 1
2
m ≥ B. 1m ≥ C. 0m ≥ D. 1
2
m >
HD: TXĐ: D R= . Để hàm số đã cho nghịch biến trên R ⇔ ( )2 2' 3 6 1 3 0y x m x m= − + − − ≤ ( x R∀ ∈ , 
dấu bằng xảy ra tại hữu hạn điểm ) 
Khi đó ( )2 2
3 0 12 1 0
' 9 1 0 2
a
m m
m m
= − <
⇔ − + ≤ ⇔ ≥  ∆ = − − ≤  
. Chọn A. 
Câu 12. Tìm tất cả các giá trị của tham số m để hàm số 4 2 22 (2 6) 4 2016y x m x m= − − + − + có đúng một 
cực trị. 
A. 3m < − B. 0m ≥ C. 3m ≥ − D. 3m ≤ −
HD: Ta có: ( )3 2
0
' 8 2 2 6 0 2 6
4
x
y x m x m
x
=

= − − + = ⇔ + =
 −
. 
Để hàm số có 1 cực trị 2 6 0 2 6 0 3
4
m
m m
+
⇔ ≤ ⇔ + ≥ ⇔ ≥ −
−
. Chọn C. 
Câu 13. Tìm m để hàm số 4 2 2( 3) 2y x m x m= − + + − có ba cực trị. 
Khóa học LUYỆN ĐỀ TRẮC NGHIỆM TOÁN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 
Chương trình Luyện thi new PRO–S Toán 2017: Giải pháp tối ưu nhất cho kì thi THPT Quốc Gia 2017! 
A. 3m > − . B. 0m ≥ . C. 3m ≥ − . D. 3m < − . 
HD: Ta có: ( )3 2
0
' 4 2 3 0 3
2
x
y x m x m
x
=

= − + = ⇔ + =

. 
Để hàm số có 3 điểm cực trị 3 0 3
2
m
m
+
⇔ > ⇔ > − . Chọn A. 
Câu 14. Tìm tất cả các giá trị của tham số m để hàm số 3 2 23( 2) 3 4 1y x m x m x m= − − + − + đồng biến trên 
tập xác định của nó. 
A. 1m < B. 1m ≥ C. 0m ≥ D. 1m ≤
HD: Ta có: D R= và ( )2 2' 3 6 2 3y x m x m= − − + . Để hàm số đồng biến trên ' 0R y x R⇔ ≥ ∀ ∈ (dấu 
bằng xảy ra tại hữu hạn điểm) 
Khi đó ( )2 2
'
3 0
4 4 0 1
' 9 2 0y
a
m m
m m
= >
⇔ − + ≤ ⇔ ≥  ∆ = − − ≤  
. Chọn B. 
Câu 15. Cho hàm số 3 23 5 2y x x x= − + − có đồ thị (C). Tìm phương trình tiếp tuyến với đồ thị (C) tại 
điểm có hệ số góc nhỏ nhất. 
A. 2 1y x= − . B. 2 2y x= − . 
C. 2y x= − . D. 2 1y x= − + . 
HD: Gọi ( )0 0;A x y là tiếp điểm. Ta xét ( ) ( )220 0 0 0' 3 6 5 3 1 2 2k y x x x x= = − + = − + ≥ . 
Khi đó tiếp tuyến có hệ số góc nhỏ nhất khi 0 01; 2 1x k y PTTT= = ⇒ = ⇒ là ( )2 1 1 2 1y x x= − + = − . 
Chọn A. 
Câu 16. Tìm m để hàm số 3 2 21 (2 3) 2 1
3
y x m x m x m= − + + − + không có cực trị. 
A. 13 mm ∨− ≥ −≤ . B. 1m ≥ − . C. 3m ≥ − . D. 3 1m− ≤ ≤ − . 
HD: Ta có ( )2 2' 2 2 3 .y x m x m= − + + 
YCBT ( ) ( )( )2 2' 2 3 0 3 3 3 0 3 1.m m m m m⇔ ∆ = + − ≤ ⇔ + + ≤ ⇔ − ≤ ≤ − Chọn D 
Câu 17. Cho hàm số 3
1 2
xy
x
=
+
. Khẳng định nào sau đây là khẳng định đúng? 
A. Đồ thị hàm số có tiệm cận ngang là y = 3. 
B. Đồ thị hàm số có tiệm cận đứng là 1x = . 
C. Đồ thị hàm số có tiệm cận ngang là 3
2
y = . 
D. Đồ thị hàm số không có tiệm cận. 
HD: ( )C có tiệm cận đứng 1
2
x = − và tiệm cận ngang 3 .
2
y = Chọn C 
Câu 18. Đồ thị sau đây là của hàm số 3 23 2y x x= − − + : 
Khóa học LUYỆN ĐỀ TRẮC NGHIỆM TOÁN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 
Chương trình Luyện thi new PRO–S Toán 2017: Giải pháp tối ưu nhất cho kì thi THPT Quốc Gia 2017! 
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Với giá trị nào của m thì phương trình 3 23 1 0x x m− − + − = có ba nghiệm phân biệt. ? 
A. 1 3m− < < . B. 3 1m− ≤ ≤ . C. 3 1m− < < . D. 1m < . 
HD: YCBT 3 23 2 1x x m⇔ − − + = + có ba nghiệm phân biệt 
⇔ đường thẳng 1y m= + cắt đồ thị hàm số 3 23 2y x x= − − + tại ba điểm phân biệt 
2 1 2 3 1.m m⇔ − < + < ⇔ − < < Chọn C 
Câu 19. Cho hàm số 3 3 2y x x= − + + có đồ thị (C). Tìm phương trình tiếp tuyến của (C) tại giao điểm 
của (C) với trục tung. 
A. 5 2y x= + . B. 2y = . C. 13 −= xy . D. 3 2y x= + . 
HD: Gọi A là giao điểm của ( )C và trục tung. 
Tọa độ A là nghiệm của hệ ( )
3 23 2 0;2 .
00
yy x x
A
xx
= = − + + 
⇔ ⇒ 
== 
Phương trình tiếp tuyến của ( )C tại A là ( ) ( ): ' 0 . 0 2.d y y x= − + 
Ta có ( )2' 3 3 ' 0 3 : 3 2.y x y d y x= − + ⇒ = ⇒ = + Chọn D 
Câu 20. Cho hàm số 3 3 3y x x= − + + có đồ thị (C). Tìm phương trình tiếp tuyến của (C) tại điểm có 
hoành độ là 1. 
A. 6 5y x= − + . B. 3y = . C. 6 5y x= + . D. 5y = . 
HD: Tiếp tuyến của ( )C tại điểm có hoành độ bằng 1, gọi điểm này là .A 
Tọa độ A là nghiệm của hệ ( )3
1 1
1;5 .
53 3
x x
A
yy x x
= = 
⇔ ⇒ 
== − + + 
Phương trình tiếp tuyến của ( )C tại A là ( ) ( ): ' 1 . 1 5.d y y x= − + 
Ta có ( )2' 3 3 ' 1 0 : 5.y x y d y= − + ⇒ = ⇒ = Chọn D 
Câu 21. Cho biểu thức 32 2K = . Hãy tìm biểu thức K được viết dưới dạng lũy thừa với số mũ hữu tỉ. 
A. 
5
32K = B. 
2
32K = C. 
4
32K = D. 
1
32K = 
HD: Ta có 
1
1 4 4 4 1 22
.
3 3 3 3 2 32.2 2 2 2 2 .K
 
= = = = = 
 
 Chọn B 
Câu 22. Tìm tất cả các giá trị thực của a để biểu thức ( )2log 7B a= − có nghĩa. 
Khóa học LUYỆN ĐỀ TRẮC NGHIỆM TOÁN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 
Chương trình Luyện thi new PRO–S Toán 2017: Giải pháp tối ưu nhất cho kì thi THPT Quốc Gia 2017! 
A. 7a > B. 7a ≤ C. 7a ≤ D. 7a < 
HD: ( )2log 7B a= − có nghĩa 7 0 7.a a⇔ − > ⇔ > Chọn A 
Câu 23. Cho 0 1.a< ≠ Tính giá trị của biểu thức 3log 2aa . 
A. 2 2 B. 3 2 C. 2 3 D. 2 
HD: Ta có ( ) ( )3 33log 2 log 2 2 2 2.a aa a= = = Chọn A 
Câu 24. Tìm tất cả các giá trị của m để phương trình 22 2 4 28 0xx m m− − + − = có nghiệm. 
A. 0∨m . 
HD: YCBT 
22 2 4 28 x x m m− −⇔ = − có nghiệm 2 0 0 1.m m m⇔ − > ⇔ < < Chọn B 
Câu 25. Tìm tập nghiệm của phương trình: 4 2 45 125x x− − = . 
A. 1
2
 
 
 
 B. { }2 C. 1
8
 
− 
 
 D. 1
16
 
− 
 
HD: ( )44 2 3 3.4 15 5 5 4 2 12 .8
x
x xPT x x x− −⇔ = = ⇔ − − = ⇔ = − Chọn C 
Câu 26. Tìm tập nghiệm của phương trình: 
2 3 105 1x x+ − = . 
A. { }2;1 B. { }2;5− C. { }2;5 −− D. { }5;2 
HD: 2
2
3 10 0
5
x
PT x x
x
=
⇔ + − = ⇔ 
= −
 Chọn B 
Câu 27. Tìm tập nghiệm của phương trình: 2( 2 1) 2 1x− = + . 
A. { }1− B. { }1 C. 






−
2
1
 D. 






2
1
HD: ( ) ( )2 2 11 12 1 2 1 1 2 1 0 .22 1
x x
PT x x
+
⇔ − = ⇔ − = ⇔ + = ⇔ = −
−
 Chọn C 
Câu 28. Tìm tập nghiệm của phương trình: 2 2 13 .2 72x x+ = . 
A. 1
4
 
 
 
 B. 3
4
 
− 
 
 C. { }1− D. { }1 
HD: ( )22 2 2 23 .2 36 3.2 36 6 6 2 2 1.xx x xPT x x⇔ = ⇔ = ⇔ = ⇔ = ⇔ = Chọn D 
Câu 29. Tìm tập nghiệm của phương trình: 2 1 2 2 2 3 2 1 2 2 23 3 3 5 9.5 5x x x x x x+ + + + ++ + − = + . 
A. { }0 B. { }1 C. { }2− D. { }3− 
HD: 2 2 2 3 2 2 2 2 23.3 3 .3 3 .3 5.5 9.5 5 .5x x x x x xPT ⇔ + + = + + 
2
2 2 339.3 39.5 1 2 0 0.
5
x
x x x x
 
⇔ = ⇔ = ⇔ = ⇔ = 
 
 Chọn A 
Khóa học LUYỆN ĐỀ TRẮC NGHIỆM TOÁN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 
Chương trình Luyện thi new PRO–S Toán 2017: Giải pháp tối ưu nhất cho kì thi THPT Quốc Gia 2017! 
Câu 30. Cho phương trình 23log (4 8 12) 2 0x x+ + − = . Trong các khẳng định sau đây khẳng định nào là 
khẳng định đúng? 
A. Phương trình có hai nghiệm dương 
B. Phương trình có một nghiệm âm và một nghiệm dương 
C. Phương trình có hai nghiệm âm 
D. Phương trình vô nghiệm 
HD: ( )2 2 23
1
2log 4 8 12 2 4 8 12 3
3
2
x
PT x x x x
x

= −
⇔ + + = ⇔ + + = ⇔ 

= −

 Chọn C 
Câu 31. Tính tổng các nghiệm của phương trình: 2 2 2
3(log 2 2).log 2 (log 2 1)
2
x x x− = − . 
A. 2
2
. B. 8 2
2
+
. C. 8 2
2
−
. D. 4 . 
HD : 
2
2
2 2
2
4log 2 3
7 3log 2 log 2 0 1 22 2 log 2
2 2
xx
PT x x
x x
==
⇔ − + = ⇔ ⇔
 = =
 
 . Chọn B. 
Câu 32. Cho khối chóp S.ABC, M và N lần lượt là trung điểm của cạnh SA, SB. Thể tích khối chóp S.ABC 
bằng 8a3. Tính thể tích của khối chóp S.MNC. 
A. 2a3. B. 1
8
a
3
. C. 1
4
a
3
. D. 1
2
a
3
. 
HD : Ta có 3.
. .
.
1 1 1 1
. . . .1 2
2 2 4 4
S MNC
S MNC S ABC
S ABC
V SM SN SC V V a
V SA SB SC
= = = ⇒ = = . Chọn A. 
Câu 33. Cho khối chóp S.ABC, M là trung điểm của cạnh SC. Tính tỉ số thể tích của khối chóp S.MAB và 
thể tích khối chóp S.ABC. 
A. 1
8
. B. 1
6
. C. 1
4
. D. 1
2
. 
HD : Ta có .
.
1 1
. . .1.1
2 2
S MAB
S CAB
V SM SA SB
V SC SA SB
= = = . Chọn D. 
Câu 34. Cho khối chóp S.ABC có SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với 
(ABC), AB = 2a và tam giác ABC có diện tích bằng 6a2. Tính thể tích khối chóp S.ABC. 
A. 2a3 . B. 6a3. C. 12a3. D. 4a3 3 . 
Khóa học LUYỆN ĐỀ TRẮC NGHIỆM TOÁN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 
Chương trình Luyện thi new PRO–S Toán 2017: Giải pháp tối ưu nhất cho kì thi THPT Quốc Gia 2017! 
HD : Gọi H là trung điểm của ( )AB SH ABC⇒ ⊥ 
Do tam giác SAB vuông cân tại S và 12
2
AB a SH AB a= ⇒ = = 
Ta có 26ABCS a= 
2 3
.
1 1
. . .6 2
3 3S ABC ABC
V SH S a a a⇒ = = = . Chọn A. 
Câu 35. Cho hình chóp S.ABC có ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của S trên (ABC) 
là điểm H thuộc cạnh BC sao cho HC = 2HB.
Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 600. 
Tính thể tích khối chóp S.ABC. 
A. 7 a3 B. 7
2
a
3
 C. 2 7
3
a
3
 D. 7
4
a
3
HD : Ta có 2 2 0 2 72 . .cos60
3
aAH BH BA BH BA= + − = 
Mặt khác ( )( )
 
 0, 60SA ABC SAH= = 
0 2 7 2 21
.tan 60 . 3
3 3
a aSH AH⇒ = = = . 
Ta có ( )
2
22 3 3
4ABC
a
S a= = 
3
2
.
1 1 2 21 2 7
. . . 3
3 3 3 3S ABC ABC
a aV SH S a⇒ = = = . Chọn C. 
Câu 36. Cho khối chóp S.ABCD có SA ⊥ (ABCD), 2SA a= và ABCD là hình vuông cạnh a . Tính bán 
kính R của mặt cầu ngoại tiếp khối chóp S.ABCD. 
A. 2R a= B. R a= C. 2R a= D. 2
2
R a= 
HD : Gọi O là giao điểm của AC và BD , qua O kẻ đường thẳng song 
song với SA cắt SC tại ( )I OI ABCD⇒ ⊥ 
I⇒ là tâm mặt cầu ngoại tiếp khối chóp .S ABCD 
Ta có 2 2 2AC AB BC a= + = 
2 2 2SC SA AC a SI a R⇒ = + = ⇒ = = . Chọn B. 
Câu 37. Cho hình chóp S.ABC có SA ⊥ (ABC), góc giữa SB và (ABC) bằng 600; tam giác ABC đều cạnh 
3a. Tình thể tích khối chóp S.ABC. 
A. 3 3 a3 B. 27
4
a
3
 C. 81
4
a
3
 D. 9 a3 
Khóa học LUYỆN ĐỀ TRẮC NGHIỆM TOÁN – Thầy ĐẶNG VIỆT HÙNG Facebook: Lyhung95 
Chương trình Luyện thi new PRO–S Toán 2017: Giải pháp tối ưu nhất cho kì thi THPT Quốc Gia 2017! 
HD : Ta có ( )( )
 
 0, 60SB ABC SBA= = 

 0
. tan 3 . tan 60 3 3SA AB SBA a a⇒ = = = 
Ta có ( )
2 23 3 9 3
4 4ABC
a aS = = 
2 3
.
1 1 9 3 27
. .3 3.
3 3 4 4S ABC ABC
a aV SH S a⇒ = = = . Chọn B. 
Câu 38. Cho khối chóp S.ABC có thể tích là 
3
3
a
. Tam giác SAB có diện tích là 22a . Tính khoảng cách d 
từ C đến mặt phẳng (SAB). 
A. d a= . B. 
2
ad = . C. 2ad = . D. 2
3
ad = . 
HD : Ta có ( )( ) 3. 23, 22S ABCSAB
V a ad C SAB
S a
= = = . Chọn B. 
Câu 39. Cho khối chóp đều S.ABCD có thể tích là 38m , điểm M là trung điểm của cạnh bên SA. Tính thể 
tích của khối chóp S.MBC ? 
A. 34m . B. 32m . C. 38
3
m . D. 31m . 
HD : Ta có 3.
. . .
.
1 1 1 1
. . .1.1 2
2 2 2 4
S MBC
S MBC S ABC S ABCD
S ABC
V SM SB SC V V V m
V SA SB SC
= = = ⇒ = = = . Chọn B. 
Câu 40. Cho khối chóp đều S.ABCD có thể tích là 38m . Diện tích tam giác SAB là 26m . Tính khoảng 
cách k từ điểm D đến mặt phẳng (SAB). 
A. 4k m= B. 2k m= C. 1k m= D. 0,5k m= 
HD : Ta có ( )( ) 3.. 2
3
3 122
, 2
6
S ABCD
S ABD
ABC ABC
VV md D SAB m
S S m
= = = = . Chọn B.