Đề thi khảo sát học sinh khá giỏi lần 2 môn Toán Lớp 11 - Đề gốc 1 - Năm học 2016-2017 - Trường THPT Lạng Giang số 1

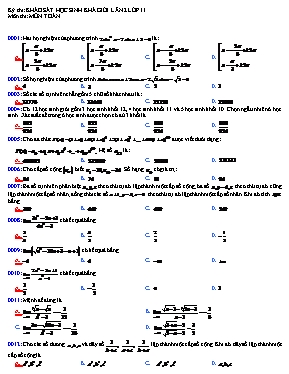
Kỳ thi: KHẢO SÁT HỌC SINH KHÁ GIỎI LẦN 2 LỚP 11
Môn thi: MÔN TOÁN
0001: Hai họ nghiệm của phương trình là:
A. 	B. 	C. 	D. 
0002: Số họ nghiệm của phương trình 
A. 	B. 	C. 	D. 
0003: Số các số tự nhiên chẵn gồm 5 chữ số khác nhau là:
A. 	B. 	C. 	D. 
0004: Có 12 học sinh giỏi gồm 3 học sinh khối 12, 4 học sinh khối 11 và 5 học sinh khối 10. Chọn ngẫu nhiên 6 học sinh. Xác suất để trong 6 học sinh được chọn có đủ 3 khối là
A. 	B. 	C. 	D. 
0005: Cho đa thức được viết dưới dạng: 
 Hệ số là:
A. 	B. 	C. 	D. 
0006: Cho cấp số cộng biết . Số hạng có giá trị:
A. 	B. 	C. 	D. 
0007: Ba số tự nhiên phân biệt theo thứ tự đó lập thành một cấp số cộng; ba số theo thứ tự đó cũng lập thành một cấp số nhân; đồng thời các số theo thứ tự đó lập thành một cấp số nhân. Khi đó tích bằng
A. 	B. 	C. 	D. 
0008: có kết quả bằng
A. 	B. 	C. 	D. 
0009: có kết quả bằng
A. 	B. 	C. 	D. 
0010: có kết quả bằng
A. 	B. 	C. 	D. 
0011: Mệnh đề đúng là
A. .	B. .
C. .	D. 
0012: Cho các số dương và dãy số lập thành một cấp số cộng. Khi đó dãy số lập thành một cấp số cộng là
A. .	B. .	C. . 	D. .
0013: Cho hàm số . Để tồn tại thì bằng
A. .	B. .	C. .	D. .
0014: Cho hàm số . Hàm số liên tục tại điểm khi tổng của bằng
A. .	B. .	C. .	D. 
0015: Cho hàm số liên tục trên đoạn sao cho , . Có thể kết luận gì về số nghiệm của phương trình trên đoạn ?
A. Không thể kết luận gì.	B. Có hai nghiệm.	C. Vô nghiệm.	D. Có ít nhất một nghiệm.
0016: Trong các mệnh đề sau. Mệnh đề sai là
A. Hai mặt phẳng cùng song song với một mặt phẳng thì song song với nhau.
B. Hai mặt phẳng song song với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều song song với mặt phẳng kia.
C. Hai mặt phẳng song song thì không có điểm chung.
D. Một mặt phẳng cắt hai mặt phẳng song song cho trước theo hai giao tuyến thì hai giao tuyến song song với nhau.
0017: Mệnh đề nào sau đây đúng
A. Nếu một mặt phẳng cắt một trong hai đường thẳng song song thì mặt phẳng đó sẽ cắt đường thẳng còn lại.
B. Hai mặt phẳng lần lượt đi qua hai đường thẳng song song thì cắt nhau theo một giao tuyến song song với một trong hai đường thẳng đó.
C. Nếu một đường thẳng cắt một trong hai đường thẳng song song thì đường thẳng đó sẽ cắt đường thẳng còn lạ
D. Hai mặt phẳng có một điểm chung thì cắt nhau theo một giao tuyến đi qua điểm chung đó.
0018: Trong các mệnh đề sau đây, mệnh đề nào đúng ?
A. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
B. Hai đường thẳng phân biệt không chéo nhau thì cắt nhau.
C. Hai đường thẳng phân biệt không song song thì chéo nhau.
D. Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau.
0019: Cho hai mặt phẳng và song song với nhau. Mệnh đề nào sau đây sai :
A. và thì .
B. Nếu đường thẳng thì 
C. Mọi đường thẳng đi qua điểm và song song với đều nằm trong .
D. Nếu đường thẳng cắt thì cũng cắt .
0020: Cho hình chóp với đáy là hình bình hành. Gọi lần lượt là trung điểm các cạnh. Gọi là điểm bất kì trên . Thiết diện của với hình chóp là:
A. Hình thang.	B. Hình bình hành.	C. Hình thoi.	D. Hình chữ nhật.
0021: Đạo hàm của hàm số là
A. .	B. .	C. .	D. .
0022: Cho hàm số . Phương trình tiếp tuyến của đồ thị tại điểm là
A. 	B. 	C. 	D. 
0023: Cho hàm số . Phương trình tiếp tuyến của biết hệ số góc của tiếp tuyến đó bằng 9 là:
A. 	B. 	C. 	D. 
0024: Tiếp tuyến của đồ thị hàm số vuông góc với đường thẳng có phương trình là
A. .	B. .	C. 	D. .
0025: Giả sử một vật rơi tự do từ trên đài quan sát của tòa nhà cách mặt đất . Biết vật đó chuyển động theo phương trình (đơn vị ), tính bằng giây. Vận tốc của vật khi chạm đất là
A. .	B. .	C. 	D. .