Đề thi học sinh giỏi vòng huyện Di Linh môn Toán lớp 9 (Năm học: 2011 – 2012)

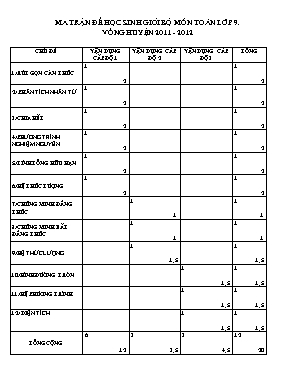
MA TRẬN ĐỀ HỌC SINH GIỎI BỘ MÔN TOÁN LỚP 9.
VÒNG HUYỆN 2011 - 2012
CHỦ ĐỀ
VẬN DỤNG 
CẤP ĐỘ 1
VẬN DỤNG CẤP ĐỘ 2
VẬN DỤNG CẤP ĐỘ 3
TỔNG
1/RÚT GỌN CĂN THỨC
1
2
1
2
2/ PHÂN TÍCH NHÂN TỬ
1
2
1
2
3/CHIA HẾT
1
2
1
2
4/PHƯƠNG TRÌNH NGHIỆM NGUYÊN
1
2
1
2
5/TÍNH TỔNG HỮU HẠN
1
2
1
2
6/HỆ THỨC LƯỢNG
1
2
1
2
7/CHỨNG MINH ĐẲNG THỨC
1
1
1
1
8/CHỨNG MINH BẤT ĐẲNG THỨC
1
1
1
1
9/HỆ THỨC LƯỢNG
1
1,5
1
1,5
10/HÌNH ĐƯỜNG TRÒN
1
1,5
1
1,5
11/HỆ PHƯƠNG TRÌNH
1
1,5
1
1,5
12/ DIỆN TÍCH
1
1,5
1
1,5
TỔNG CỘNG
6
12
3
3,5
3
4,5
12
20
PHỊNG GIÁO DỤC & VÀ ĐÀO DI LINH
 ĐỀ CHÍNH THỨC 
ĐỀ THI HỌC SINH GIỎI VÒNG HUYỆN
MÔN TOÁN LỚP 9
Thời gian làm bài : 150 phút (không kể thời gian phát đề )
(Năm học: 2011 – 2012)
Câu1 :(2đ) Rút gọn A = 
Câu 2 :(2đ) Phân tích đa thức x3 – 19x – 30 thành nhân tử
Câu 3 :(1,5đ) Chứng minh n(31n2 -1 ) chia hết cho 6 với mọi số nguyên n
Câu 4 :(2đ) Cho tam giác ABC vuơng tại A cĩ hai đường trung tuyến BD và AE vuơng gĩc với nhau(D, E lần lượt trung điểm của AC và BD) Biết AB = cm. Tính BC
Câu 5 :(1,5đ) Tính tích 
Câu 6 :(2đ) Giải hệ phương trình 
Câu 7 : (1,5đ) Tìm nghiệm nguyên của phương trình : x2 – 4x +2y – xy + 9 = 0 
Câu 8 :(1,5đ) Cho hình bình hành ABCD, kẻ BFAD, BECD (F thuộc AD, E thuộc CD). Chứng minh DC.EC = AD.FA
Câu 9 :(1,5đ) Cho nửa đường trịn đường kính AB, trên cùng nửa mặt phẳng với nửa đường trịn bờ AB kẻ hai tiếp tuyến Ax;By với nửa đường trịn (A;B là tiếp điểm). Từ điểm M thuộc nửa đường trịn (M khác A;B) kẻ tiếp tuyến thứ ba với nửa đường trịn cắt Ax và By lần lượt tại C và D, gọi I là giao điểm của AD và BC. Chứng minh MI song song BD .
Câu 10 :(1,5đ) Cho và . Chứng minh:
Câu 11 :(1,5đ) Cho hình bình hành ABCD . Gọi M là trung điểm của AD, BM cắt AC tại K . Tính . 
Câu 12 :(1,5đ) Cho a > 0; b > 0 và a + b = 1. Chứng minh : 
 HẾT 
Thí sinh không được sử dụng máy tính
ĐÁP ÁN CHÍNH THỨC ĐỀ THI HỌC SINH GIỎI VÒNG HUYỆN
MÔN TOÁN LỚP 9
(Năm học: 2011 – 2012)
Câu1 :(2đ) Rút gọn A = 
	 (0,5 điểm)
	(0,5 điểm)
=	(0,5 điểm)
= 1	(0,5 điểm)
Câu 2 :(2đ) Phân tích đa thức x3 – 19x – 30 thành nhân tử
= (x + 2)(x2 – 2x – 15)	(1 điểm)
= (x + 2)(x + 3)(x – 5)	(1 điểm)
Câu 3 :(1,5đ) Chứng minh n(31n2 -1 ) chia hết cho 6 với mọi số nguyên n
Ta cĩ: n(31n2 -1 ) = n(30n2 + n2 – 1) 	(0,5 điểm)
 = (n – 1)n(n + 1) + 30n2	(0,5 điểm)
Kết luận	(0,5 điểm)
Câu 4 :(2đ) Cho tam giác ABC vuơng tại A cĩ hai đường trung tuyến BD và AE vuơng gĩc với nhau(D, E lần lượt trung điểm của AC và BD) Biết AB = cm. Tính BC
Ta cĩ: BG.BD = AB2 	(0,5 điểm)	
=> BD2 = 12 => BD2 = 18 	(0,5 điểm)	 
=> AD2 = 6	
=> AC2 = 24 G	(0,5 điểm)	
=> BC = 6(cm)	(0,5 điểm)
Câu 5 :(1,5đ) Tính tích 	
	(0,5 điểm)
	(0,5 điểm)
	(0,5 điểm)
Câu 6 :(2đ) Giải hệ phương trình 
ĩ 	(0,5điểm)	
Giải hpt : cĩ nghiệm là 	 (0,25điểm )
Giải hpt : cĩ 2 nghiệm : (1,-2) ; (-2;1) 	 (0,5điểm)
Kết luận : 	 (0,25điểm
Câu 7 : (1,5đ) Tìm nghiệm nguyên của phương trình : x2 – 4x +2y – xy + 9 = 0 
 (x – 2)(x – y – 2) = –5	 (0,5 điểm)
Mà –5 = (–5)(1) = (1)(–5) = (5)(–1) = (–1)(5) 
Từ đĩ ta cĩ bốn nghiệm (x; y) = (–3;–6); (3; 6);(7;6);(1;- 6)	 (1 điểm)
Câu 8 :(1,5đ) Cho hình bình hành ABCD, kẻ BFAD, BECD (F thuộc AD, E thuộc CD). Chứng minh DC.EC = AD.FA
FBA đồng dạng với EBC (g-g) 	 (0,5 điểm)
	 (0,5 điểm)
	 (0,5 điểm) 
Câu 9 :(1,5đ) Cho nửa đường trịn đường kính AB, trên cùng nửa mặt phẳng với nửa đường trịn bờ AB kẻ hai tiếp tuyến Ax;By với nửa đường trịn (A;B là tiếp điểm). Từ điểm M thuộc nửa đường trịn (M khác A;B) kẻ tiếp tuyến thứ ba với nửa đường trịn cắt Ax và By lần lượt tại C và D, gọi I là giao điểm của AD và BC. Chứng minh MI song song BD .
C/m : AC//BD => 	(0,5 điểm)
Lí luận chỉ ra : 	(0,5 điểm)
=>	(0,5 điểm)
Câu 10 :(1,5đ) Cho và . Chứng minh:
Ta cĩ: 
 	(0,5điểm)
 	(0,5điểm)
Lập luận ra được 	(0,5điểm)
Câu 11 :(1,5đ) Cho hình bình hành ABCD . Gọi M là trung điểm của AD, BM cắt AC tại K . Tính . 
Chứng minh SAKM = 	(0,5điểm)
Chứng minh SAOD = 	(0,5điểm)
Suy ra SAKM = 	(0,5điểm)
Câu 12 :(1,5đ) Cho a > 0; b > 0 và a + b = 1. Chứng minh : 
x,y > 0 ta cĩ 	(0,75 điểm)
 	(0,75 điểm)
Học sinh làm cách khác đúng giám khảo phân bước tương ứng cho điểm.