Đề ôn tập thi học sinh giỏi Hình học: lớp 7

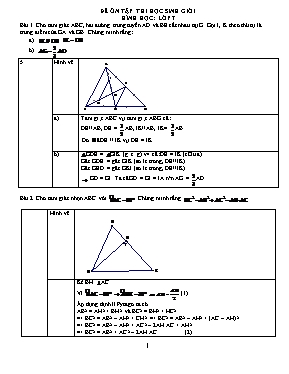
ĐỀ ễN TẬP THI HỌC SINH GIỎI 
HèNH HỌC: LỚP 7
Bài 1. Cho tam giỏc ABC, hai đường trung tuyến AD và BE cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GA và GB. Chứng minh rằng:
; 
5
Hỡnh vẽ
a)
Tam giác ABC và tam giác ABG có:
DE//AB, DE = AB, IK//AB, IK= AB
 Do đó DE // IK và DE = IK
b)
GDE = GIK (g. c. g) vì có: DE = IK (câu a)
Góc GDE = góc GIK (so le trong, DE//IK)
Góc GED = góc GKI (so le trong, DE//IK)
 GD = GI. Ta có GD = GI = IA nên AG = AD.
Bài 2. Cho tam giỏc nhọn ABC với . Chứng minh rằng 
Hỡnh vẽ
Kẻ BH AC
Vỡ (1)
Áp dụng dịnh lớ Pytago ta cú
AB2 = AH2 + BH2 và BC2 = BH2 + HC2
=> BC2 = AB2 – AH2 + CH2 => BC2 = AB2 – AH2 + (AC – AH)2
=> BC2 = AB2 – AH2 + AC2 – 2AH.AC + AH2 
=> BC2 = AB2 + AC2 – 2AH.AC (2)
Từ (1) và (2: 
Bài 3. Cho tam giỏc ABC cú đường cao AH bằng nửa cạnh BC. Trờn nửa mặt phẳng bờ AB chứa C vẽ tia Bx sao cho trờn tia Bx lấy điểm D sao cho BD =BA. Kẻ phõn giỏc BF của gúc ABD 
Tớnh cỏc gúc chưa biết của tam giỏc ABD
Chứng minh AB=BD=DA
Chứng minh AC =CB
Hỡnh vẽ
a)
Vẽ phõn giỏc BF của ABD chứng minh: ABF= DBF (c-g-c) 
Từ đú nhờ định lý tổng ba gúc trong tam giỏc chứng minh: 
b)
Kẻ phõn giỏc AI dựa vào định lý tổng 3 gúc trong tam giỏc chứng minh 
 Từ đú chứng minh Suy ra AB=AD 
Mà theo giải thiờt: AB=BD nờn AB=BD=DA
c)
Gọi E là trung điểm của BC, chứng minh: 
Từ đú chứng minh 
Chứng minh rồi chứng minh 
Chứng minh 
Chứng minh 
Bài 4. Cho , gọi M và N theo thứ tự là trung điểm của AC và AB. Trờn tia đối cả tia MB lấy điễm D sao cho MD = MB, trờn tia đối của tia NC lấy điểm E sao cho NE = NC. Chứng minh rằng:
Ba điểm E, A, D thẳng hàng.
A là trung điểm của ED.
Hỡnh vẽ
a)
Từ (1) và (2) thẳng hàng
b)
Từ chứng minh trờn A là trung điểm của ED