Đề kiểm tra Đại số 11 chương IV

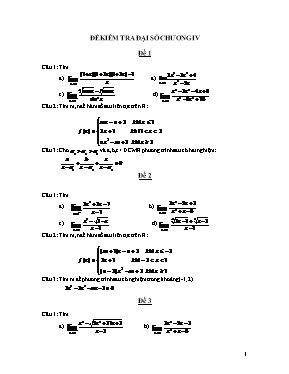
ĐỀ KIỂM TRA ĐẠI SỐ CHƯƠNG IV
Đề 1
Câu 1: Tìm
	a) a) 
	c) d) 
Câu 2: Tìm m,n để hàm số sau liên tục trên R:
Câu 3: Cho và a,b,c < 0 CMR phương trình sau có hai nghiệm:
Đề 2
Câu 1: Tìm
	a) b) 
	c) d) 
Câu 2: Tìm m,n để hàm số sau liên tục trên R:
Câu 3: Tìm m để phương trình sau có nghiệm trong khoảng (-1;2)
Đề 3
Câu 1: Tìm
	a) 	b) 
	c) d) 
Câu 2: Tìm m,n để hàm số sau liên tục trên R:
Câu 3: Tìm m để phương trình sau có nghiệm thuộc khoảng 
Đề 4
Câu 1: Tìm
	a) 	 b) 
	c) d) 
Câu 2: Tìm m,n để hàm số sau liên tục trên R:
Câu 3: Cho và a,b,c < 0 CMR phương trình sau có hai nghiệm:
Đề 5
Câu 1: Tìm
	a) 	b) 
	c) d) 
Câu 2: Tìm a, b để hàm số sau liên tục trên R
Câu 3: Cho và a,b,c < 0 CMR phương trình sau có hai nghiệm:
Đề 6
Câu 1: Tìm 
	a) b) 
	c) 	 c) 
Câu 2: Tìm m,n để hàm số sau liên tục trên R
Câu 3: Tìm m để phương trình sau có nghiệm thuộc khoảng (-2;3)
Đề 7
Câu 1(6đ):Tìm
	a) b) 
	c) 	 d) 
Câu 2(3đ): Với giá trị nào của a thì hàm số sau liên tục trên biết:
Nếu 
Nếu 
Câu 3(1đ): Chứng minh rằng phương trình sau luôn có nghiệm:
Đề 8
Câu 1: (6 điểm) Tìm các giới han sau:
	a) 
	b) 
 c) 	 	 
Câu 2: (3điểm) Cho hàm số: , Tìm m để hàm số liên tục tại x = 2.
 Câu 3:( 1điểm) Cho phương trình: , m là tham số
CMR phương trình trên luôn có ít nhất một nghiệm dương với mọi giá trị của tham số m
Đề 9
Câu 1(2điểm): Tính các giới hạn sau:
	a/ limn+44+3n-n2	b/ lim3n+12+n2
Câu 2(2điểm): Tính các giới hạn sau:
	a/ limx→3x2-7x+12x-3	b/ limx→4x+5-3x-4
Câu 3(5điểm):
 a/ Cho hàm số: y=fx=x2+3x+2x+2 (x<2)3ax-5 (x≥2) 
	Định m để hàm số liên tục trên R.
 b/ Chứng minh phương trình: x3+3x2-1=0 có nghiêm trên(-2;2).
 c/ Định m để phương trình: m-3x4+3m+1x2+3m2-m-4=0
có nghiệm trên khoảng (-1;0).
Đề 10
Bài 1. ( 6 điểm) Tìm các giới hạn sau:
	1) 	2) 	
 3)	 4) 
Bài 2. ( 4 điểm)
	1) Xét tính liên tục của hàm số sau trên tập xác định của nó:
	2) Chứng minh rằng phương trình sau có ít nhất hai nghiệm : .