Đề kiểm tra chương III - Hình học 8 năm học 2016 – 2017

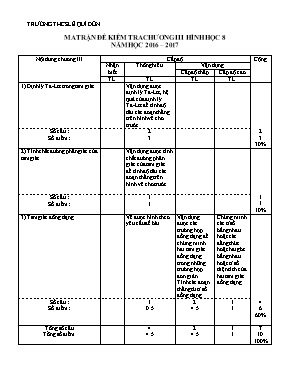
TRƯỜNG THCS LÊ QUÍ ĐÔN
MA TRẬN ĐỀ KIỂM TRA CHƯƠNG III HÌNH HỌC 8
NĂM HỌC 2016 – 2017 
Nội dung chương III
Cấp độ
Cộng
Nhận biết
Thông hiểu
Vận dụng
Cấp độ thấp
Cấp độ cao
TL
TL
TL
TL
1) Định lý Ta-Let trong tam giác
Vận dụng được định lý Ta-Let , hệ quả của định lý 
Ta-Let để tính độ dài các đoạn thẳng trên hình vẽ cho trước .
2
3
30%
Số câu :
Số điểm :
2
3
2) Tính chất đường phân giác của tam giác
Vận dụng được tính chất đường phân giác của tam giác để tính độ dài các đoạn thẳng trên hình vẽ cho trước .
1
1
10%
Số câu :
Số điểm :
1
1
3) Tam giác đồng dạng
Vẽ được hình theo yêu cầu đề bài .
Vận dụng được các trường hợp đồng dạng để chứng minh hai tam giác đồng dạng trong những trường hợp đơn giản .
Tính các đoạn thẳng từ tỉ số đồng dạng .
Chứng minh các tỉ số bằng nhau hoặc các đẳng thức hoặc hai góc bằng nhau hoặc tỉ số diện tích của hai tam giác đồng dạng .
4
6
60%
Số câu :
Số điểm :
1
0.5
2
4.5
1
1
Tổng số câu
Tổng số điểm
4
4.5
2
4.5
1
1
7
10
100%
KIỂM TRA CHƯƠNG III HÌNH HỌC LỚP 8 NĂM HỌC 2016-2017
Thời gian làm bài 45 phút
Bài 1(4 điểm)
Tính các độ dài x, y trong mỗi hình vẽ sau:
	 Hình 2
 Hình 1
 Hình 3
 ( AD là phân giác của góc BAC)
 Bài 2(6điểm): Cho tam giác ABC vuông tại A có AB = 12 cm, AC = 16 cm. Vẽ đường cao AH.
	a) Chứng minh HBA ഗ ABC
	b) Tính BC, AH, BH.
	c)Tia phân giác của góc B cắt AC và AH theo thứ tự ở M và N.Kẻ HI song song với BN (IAC).Chứng minh AN2=NI.NC
ĐÁP ÁN VÀ BIỂU ĐIỂM
Bài
Câu
Nội dung
Điểm
1
1a
Hình 1
Vì ABC có MN // BC 
( định lí Ta-lét)	
1đ
(0,25đ)
(0,25đ)
(0,5đ)
1b
Hình 2:
Vì AB // DE (hệ quả của định lí Ta-let)	
Hay 	
Suy ra : 	
2đ
(0,5đ)
(0,5đ)
(0,5đ)
(0,5đ)
1c
Hình 3:
ABC có BD là tia phân giác của góc BAC
 (T/c đường phân giác trong tam giác)	
(T/c của dãy tỉ số bằng nhau)	
Vậy DB = 3.2 = 6 
 ( Học sinh trình bày cách khác vẫn cho trọn điểm)
1đ
(0,25đ)
(0,25đ)
(0,25đ)
(0,25đ)
3
Hình vẽ 
0,5đ
a
a) Chứng minh HBA ഗ ABC
 HBA và ABC có:
 = = 900(gt)
 chung
Do đó HBA ABC (g.g)
1,5đ
0,5đ
0,5đ
0,5đ
b
 vuông tại A (gt) 
 BC2 = AB2 + AC2 
 BC = 
cm
* Vì vuông tại A nên: 
=> (cm)
* HBA ABC(cmt)
=> 
=>= = 7,2 (cm)
 ( Học sinh trình bày cách khác vẫn cho trọn điểm)
3đ
0,25đ
0.25đ
0,25đ
0,25đ
0,5đ
0,5đ
0,5đ
0,5đ
c
Ta có AHI có HI//MN (HI//BN) 
 (định lí ta let)
Mà (vì BM là phân giác của góc B của tam giác ABH)
 (ABC HBA)
 ( vì BN là phân giác của góc B của tam giác ABC)
Suy ra 
 ( Học sinh trình bày cách khác vẫn cho trọn điểm)
1đ
0,25đ
0,25đ
0,25đ
0,25đ