Đề đề xuất kiểm tra học kỳ I năm học 2015 – 2016 môn Toán 9

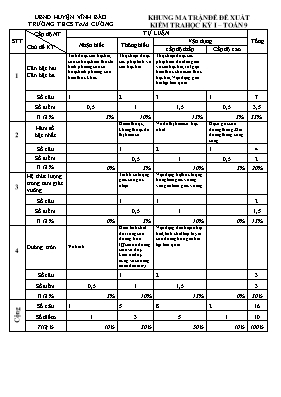
UBND HUYỆN VĨNH BẢO
KHUNG MA TRẬN ĐỀ ĐỀ XUẤT 
TRƯỜNG THCS TAM CƯỜNG
KIỂM TRA HỌC KỲ I – TOÁN 9
STT
 Cấp độ NT
Chủ đề KT
TỰ LUẬN
Tổng
Nhận biết
Thông hiểu
Vận dụng
cấp độ thấp
Cấp độ cao
1
Căn bậc hai.
Căn bậc ba
Tính được căn bậc hai, của số hoặc biểu thức là bình phương của số hoặc bình phương của biểu thức khác
Thực hiện được các phép tính về căn bậc hai
Thực hiện được các phép biến đổi đơn giản về căn bậc hai, rút gọn biểu thức chứa căn thức bậc hai, Vận dụng giải bài tập liên quan
Số câu
1
2
3
1
7
Số điểm
0,5
1
1,5
0,5
3,5
Tỉ lệ %
5%
10%
15%
5%
35%
2
Hàm số 
bậc nhất
Điểm thuộc, không thuộc đồ thị hàm số
Vẽ đồ thị hàm số bậc nhất
Hệ số góc của đường thẳng. Hai đường thẳng song song
Số câu
1
2
1
4
Số điểm
0,5
1
0,5
2
Tỉ lệ %
0%
5%
10%
5%
20%
3
Hệ thức lượng trong tam giác vuông
Tính tỉ số lượng giác của góc nhọn
Vận dụng hệ thức lượng trong tam giác vuông vào giải tam giác vuông 
Số câu
1
1
2
Số điểm
0,5
1
1,5
Tỉ lệ %
0%
5%
10%
0%
15%
4
Đường tròn
Vẽ hình
Hiểu tính chất đối xứng của đường tròn (Quan hệ đường kính và dây; Liên hệ dây cung và khoảng cách đến tâm)
Vận dụng dấu hiệu nhận biết, tính chất tiếp tuyến của đường tròn giải bài tập liên quan
Số câu
1
2
3
Số điểm
0,5
1
1,5
3
Tỉ lệ %
5%
10%
15%
0%
30%
Cộng
Số câu
1
5
8
2
16
Số điểm
1
3
5
1
10
Tỉ lệ %
10%
30%
50%
10%
100%
UBND HUYỆN VĨNH BẢO
ĐỀ ĐỀ XUẤT KIỂM TRA HỌC KỲ I 
TRƯỜNG THCS TAM CƯỜNG
NĂM HỌC 2015 – 2016
MÔN TOÁN 9
(Đề có 01 trang)
Thời gian làm bài 90 phút
Bài 1. (1,5 điểm) Thực hiện phép tính:
a) b) c/ 
Bài 2. (1,5 điểm) Cho biểu thức: 
 	 P = (Với x > 0; x 1; x4)
 a/ Rút gọn P.
 b/ Với giá trị nào của x thì P có giá trị bằng
 c/ Tính giá trị của P tại 
Bài 3. (2 điểm) Cho đường thẳng (d): y = (m + 4)x - m + 6 (m là tham số)
Tìm m để đường thẳng (d) đi qua điểm A(-1; 2).
Vẽ đường thẳng (d) với giá trị tìm được của m ở câu a).
Tìm m để đường thẳng (d) song song với đường thẳng y = -2x + 3.
CMR: Khi m thay đổi thì đường thẳng (d) luôn đi qua một điểm cố định.
Bài 4. (4,5 điểm) Cho nửa (O), đường kính AB = 2R và dây AC = R.
Chứng minh rABC vuông 
Giải rABC.
Gọi K là trung điểm của BC. Qua B vẽ tiếp tuyến Bx với (O), tiếp tuyến này cắt tia OK tại D. Chứng minh DC là tiếp tuyến của (O).
Tia OD cắt (O) ở M. Chứng minh OBMC là hình thoi.
Vẽ CH vuông góc với AB tại H và gọi I là trung điểm của CH. Tiếp tuyến tại A của (O) cắt tia BI tại E. Chứng minh E, C, D thẳng hàng.
Bài 5. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức sau: A = 
-------------Hết--------------
UBND HUYỆN VĨNH BẢO
HƯỚNG DẪN CHẤM ĐỀ XUẤT KIỂM TRA HK I
TRƯỜNG THCS TAM CƯỜNG
MÔN TOÁN LỚP 9
Bài
Đáp án sơ lược
Cho điểm
Cộng
1.a
= =
0,25x2
0,5
1.b
= =
0,25x2
0,5
1.c
 = 
0,25x2
0,5
2.a
0,25x2
0,5
2.b
P = = Û = 8 
 x = 64 (TMĐK)
0,25
0,25
0,5
2.c
= TMĐK. Tính 
Thay vào P và tính đúng được 
0,25
0,25
0,5
3.a
Thay đúng x=-1; y=2 vào y = (m + 4)x - m + 6 
 Tính đúng được m = 0
0,25
0,25
0,5
3.b
Với m = 0 ta có y = 4x+6. Chỉ ra được 2 điểm thuộc (d)
Vẽ đúng (d): y = 4x+6
0,25
0,25
0,5
3.c
Chỉ ra đ/k: m+4=-2 và 6-m=3
Tính được m=-6 
0,25
0,25
0,5
3.d
(d) luôn đi qua điểm cố định I(x0; y0) Û y0=(m+4)x0-m+6 
 Tính được (x0; y0) =(1;10)
0,25
0,25
0,5
4
Hình vẽ đúng ( cho câu a)
0,5
0,5
4a
rABC nội tiếp đường tròn đường kính AB
nên rABC vuông tại C
0,25x2
0,5
4b
Tính được BC = 
ÐB = 300; ÐA = 600
0,5
0,25x2
1
4c
Khẳng định OD ^BC
C/m rOBD = rOCD
Suy ra OC ^ CD 
Suy ra DC là tiếp tuyến tại C của (O).
0,25x4
1
4d
C/m được K là trung điểm của OM
Suy ra OCMB là hình bình hành
Mà OM ^ CB nên OCMB là hình thoi
0,25x3
0,75
4e
Gọi F là giao điểm của BC và AE. C/m được AE = EF
C/m được ECO = 900
Suy ra ECD = 1800 nên E; C; D thẳng hàng
0,25x3
0,75
5
ĐK: x1, = 
Vậy MinA = 3 Û x = 2(t/m)
0,25
0,25
0,5
Chú ý: HS làm cách khác đúng vẫn cho điểm tối đa.