Đáp án đề thi học sinh giỏi Vật lí lớp 9 - Năm học 2009-2010 - Sở GD & ĐT Nghệ An

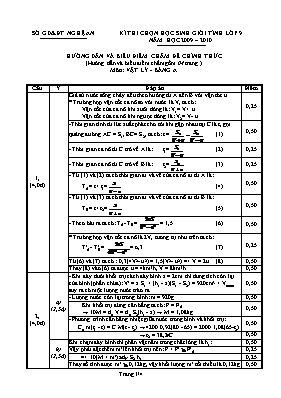
SỞ GD&ĐT NGHỆ AN
KÌ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9
NĂM HỌC 2009 – 2010
HƯỚNG DẪN VÀ BIỂU ĐIỂM CHẤM ĐỀ CHÍNH THỨC
(Hướng dẫn và biểu điểm chấm gồm 04 trang )
Môn: VẬT LÝ - BẢNG A
Câu
Ý
Đáp án
Điểm
1,
(4,0đ)
Giả sử nước sông chảy đều theo hướng từ A đến B với vận tóc u.
* Trường hợp vận tốc ca nô so với nước là V, ta có:
	Vận tốc của ca nô khi xuôi dòng là: V1= V+ u.
	Vận tốc của ca nô khi ngược dòng là: V2= V- u.
0,25
-Thời gian tính từ lúc xuất phát cho tới khi gặp nhau tại C là t, gọi quảng đường AC = S1, BC= S2, ta có:	t = 	(1)
0,50
- Thời gian ca nô từ C trở về A là:	t1=	(2)
0,25
- Thời gian ca nô từ C trở về B là:	t2=.	(3)
0,25
- Từ (1) và (2) ta có thời gian đi và về của ca nô đi từ A là: 
	TA= t+ t1=	(4)
0,50
- Từ (1) và (3) ta có thời gian đi và về của ca nô đi từ B là: 
	TB= t+ t2=	(5)
0,50
- Theo bài ra ta có: TA- TB= = 1,5	(6)
0,50
* Trường hợp vận tốc ca nô là 2V, tương tự như trên ta có:
	T'A- T'B= = o,3	(7)
0,25
Từ (6) và (7) ta có : 0,3(4V2- u2) = 1,5(V2- u2) => V = 2u	(8)
0,50
Thay (8) vào (6) ta được u = 4km/h, V = 8km/h.
0,50
2,
(4,0đ)
a)
(2,5đ)
- Khi đáy dưới khối trụ cách đáy bình x = 2cm thì dung tích còn lại của bình (phần chứa): V' = x.S1 + (h1 - x)(S1 - S2) = 920cm3 < Vnước
suy ra có một lượng nước trào ra
0,50
- Lượng nước còn lại trong bình: m = 920g
0,50
Khi khối trụ đứng cân bằng ta có: P = FA
Þ 10M = dn.V = dn.S2(h1 - x) Þ M = 1,08kg
0,50
- Phương trình cân bằng nhiệt giữa nước trong bình và khối trụ:
 Cn.m(t1 - t) = C.M(t - t2) Þ 4200.0,92(80 - 65) = 2000.1,08(65-t2)
0,50
	 Þ t2 = 38,20C
0,50
b)
(2,5đ)
Khi chạm đáy bình thì phần vật nằm trong chất lỏng là h1:
0,50
Vậy phải đặt thêm m' lên khối trụ nên: P + P' F'A
0,25
 => 10(M + m')dN.S2.h1
0,25
Thay số tính được m' 0,12kg, vậy khối lượng m' tối thiểu là 0,12kg
0,50
3,
(4,0đ)
a)
(2,25đ)
Điện trở tương đương của mạch:
R= R1+ RMN = R1+ Thay số ta tính được: R= 40.
0,50
- Dòng điện chạy qua R1 là I1= I= Thay số tính được: I1= I= 1,5A
0,50
- Vì: (R2+R3) = (R4+R5) nên I2= I4= 0,5I = 0,75A
0,50
- Hiệu điện thế trên R2 và trên R4 tương ứng là:
 U2= I2R2= 0,75.20= 15V, U4= I4R4= 0,75.40= 30V.
0,50
- Vậy số chỉ của vôn kế là UV= U4- U2 = 15V
0,25
b)
(1,75đ)
- Thay vôn kế bằng bóng đèn dòng điện qua đèn ID= 0,4A có chiều từ P đến Q, nên: I3= I2 - 0,4; I5= I4+ 0,4	
0,25
Mà U2+ U3= U4 + U5 => 20I2+ 40(I2- 0,4) = 40I4+ 20(I4+ 0,4)
0,50
=> I2= I4+ 0,4 ; I = I2+ I4 = 2I4+ 0,4
0,25
Mặt khác: U1+ U4 + U5= U => 10(2I4+ 0,4)+ 40I4+ 20(I4+ 0,4) = 60	=> I4 = 0,6A ; I2 = 1A
Hiệu điện thế hai đầu bóng đèn là: UD= U4 - U2 = 40.0,6 - 20.1= 4V
0,50
Điện trở của đèn là: RD= = = 10
0,25
4,
(4,0đ)
a)
(2,5đ)
- Điện trở toàn mạch: R= r + RAB = r + 
0,50
- Dòng điện mạch chính: I=
0,25
Từ hình vẽ ta có: U2= UAB=I.RAB= 
0,25
- Công suất trên R2 : P2= = 
0,50
Vận dụng bất đẳng thức côsi ta có:
	P2 = 
0,25
Vậy P2MAX= Khi R2(r +R1) = rR1 => R2 = 	(1)
0,25
Mặt khác theo bài ra ta có: = =>.= 
	 => = => R1=3R2	(2)
0,25
Từ (1) và (2) Giải ra ta có: R2= 2; R1=6
0,25
b)
(1,5đ)
Thay R2 bằng đèn. Từ hình vẽ ta có:
	Cường độ dòng điện mạch chính . I =
0,25
Công suất trên AB: PAB= I2.RAB => PAB= 	=> PABMAX= Khi r=RAB = 3
0,50
Mặt khác RAB= = 3 => =3 => Rd = 6
0,25
Do Rd=R1 => Pd=P1===3W
0,25
Mặt khác vì RAB= r => Ud=UAB==6V
0,25
5,
(4,0đ)
Ta xét với 3 trường hợp:
a/ Với là góc nhọn:
Góc INI’ hợp giữa hai pháp tuyến cũng bằng . Vận dụng định lí về góc ngoài của một tam giác đối với tam giác II’N: i = i’+ (hình a)
Đối với II’B: 2i = 2i’+. Từ đó suy ra: = 2.
0,50
Có thể xảy ra trường hợp giao điểm N giữa hai pháp tuyến nằm trong góctạo bởi hai gương (hình b).
Chứng minh tương tự ta vẫn có= 2.
0,50
b/ Trường hợp là góc tù (hình c):
	Với DII’O: = i +i’
	Với DII’B: =2(900- i + 900- i’) = 3600- 2(i + i’)
	Từ đó suy ra: = 3600- 2
0,50
c/ Trường hợp = 900
	Dễ dàng nhận thấy các tia SI và I’R song song và ngược chiều nhau, ta chứng minh được= 1800 (hình d)
0,50
G2
Hình a
Hình b
S
R
b
G1
a
b
 i
i
i' i
S
G2
G1
Hình c
S
R
b
O
i'
i
R
S
G2
Hình d
G2
G1
G1
Lưu ý: Mỗi hình vẽ đúng cho 0,50 điể
m
2,00
Chú ý: Nếu thí sinh giải theo cách khác đúng vẫn cho điểm tối đa
- - - Hết - - -