63 câu toán giải tích 12 chương I

63 câu TOÁN GIẢI TÍCH 12 CHƯƠNG I 
0001: Hàm số 
3 21 1
3 2
m
y x x m x đạt cực đại tại 1x khi 
A. 2m B. 2m C. 2m D. 2m 
0002: Cho hàm số 
4 33 4y x x . Khẳng định nào sau đây đúng 
A. Hàm số không có cực trị B. Hàm số đạt cực đại tại gốc tọa độ 
C. Hàm số đạt cực tiểu tại gốc tọa độ D. Điểm 1; 1A là điểm cực tiểu 
0003: Đồ thị hàm số 
2
2 1
3 2
x
y
x x
 có 
A. Một đường tiệm cận B. Hai đường tiệm cận C. Ba đường tiệm cận D. Không có tiệm cận 
0004: Cho đường cong 3y x x ( )C . Phương trình tiếp tuyến của ( )C tại điểm 1;0A là 
A. 2 2y x B. 2 2y x C. 2 2y x D. 2 2y x 
0005: Tiệm cận ngang của đồ thị hàm số 
2
3x 2
x
y là 
A. 
1
3
y B. 
1
3
x C. 
1
3
y D. 
1
3
x 
0006: Hàm số nào sau đây có cực đại 
A. 
2
2
x
y
x
 B. 
2
2
x
y
x
 C. 
2
2
x
y
x
 D. 
2
2
2
x
y
x
0007: Đường thẳng y m cắt đồ thị hàm số 4 2y x x tại bốn điểm phân biệt khi và chỉ khi 
A. 
1
0
4
m B. 
1
0
4
m C. 
1
4
m D. 0m 
0008: Tâm đối xứng của đồ thị hàm số 
2 1
1
x
y
x
 là 
A. 2;1 B. 1;2 C. 1;2 D. 2; 1 
0009: Đồ thị hàm số nào sau đây không có điểm uốn 
A. 
3 21 43
3 3
y x x x B. 3 23 3y x x 
C. 
3 2y x x D. 2 3 1y x x 
0010: Đồ thị sau đây là đồ thị của hàm số nào? 
A. 
4 32xy x B. 4 22y x x C. 3 22y x x D. 
2
1
x
y
x
0011: Tập xác định của hàm số 
2 1
2
x
y
x
 là: 
A. D B. ;2 2;D 
C. ; 2 2;D D. \ 2D 
0012: Phương trình tiếp tuyến với đồ thị hàm số ( )y f x tại điểm 
0 0
( ; )M x y có dạng là: 
A. 
0
'
0 0
.
x
y f x x y B. 
0
'
0 0
.
x
y f x x y C. 
0
'
0 0
.
x
y f x x y D. 
0
'
0 0
.
x
y f x x y 
0013: Đồ thị hàm số: 
2 5
3
x
y
x
 Có bao nhiêu điểm cực trị? 
A. 0 B. 1 C. 2 D. 3 
0014: Đồ thị hàm số 
3 23 4y x x có bao nhiêu đường tiệm cận: 
A. 1 B. 0 C. 2 D. 4 
0015: Phương trình hoành độ giao điểm của hai đồ thị hàm số ( )y f x và ( )y g x là: 
A. '( ) '( )f x g x B. ( ) ( )f x g x C. '( ) 0f x D. '( ) 0g x 
0016: Tập xác định của hàm số 
3 23 4y x x là: 
A. ;0D B. 0;D C. D D. \ 0D 
0017: Cho hàm số 
2 3
2
x
y
x
 chọn câu trả lời đúng 
A. 
2
lim
x
y B. 
2
lim
x
y C. 
2
lim
x
y D. 
2
lim
x
y 
0018: Cho hàm số 
3 23 3y x x chọn câu trả lời đúng 
A. lim
x
y B. lim 0
x
y C. lim 0
x
y D. lim
x
y 
0019: Trong các hàm số sau, hàm số nào nghịch biến trên R: 
A. 
4 22 1y x x B. 
3 1
1
x
y
x
C. 
3 22 1y x x D. 3 22 10 1y x x x 
0020: Đồ thị hàm số: 
4 21 2 6
4
y x x Có bao nhiêu điểm cực tiểu? 
A. 3 B. 1 C. 2 D. 0 
0021: Đồ thị hàm số 
2 1
2
x
y
x
 có bao nhiêu đường tiệm cận: 
A. 1 B. 2 C. 0 D. 4 
0022: Phương trình tiếp tuyến với đồ thì hàm số 
3 1
1
x
y
x
 tại điểm 1;2M là: 
A. 1y x B. 1y x C. 
1 3
2 2
y x D. 
1 3
2 2
y x 
0023: Giá trị lớn nhất và nhỏ nhất của hàm số 
4 22 3y x x trên đoạn 0;2 là: 
A. 
0;2 0;2
max 15; min 2y y B. 
0;2 0;2
max 11; min 2y y 
C. 
0;2 0;2
max 11; min 2y y D. 
0;2 0;2
max 15; min 2y y 
0024: Phương trình tiếp tuyến với đồ thì hàm số 3 23 1y x x tại điểm có hoành độ 
0
1x là 
A. 9 6y x B. 9 6y x C. 9 6y x D. 9 6y x 
0025: Hàm số: 
4 2 22 1y x m x m Có ba điểm cực trị thì: 
A. 1;m B. ;1m C. 1;m D. ; 1m 
0026: Hàm số 3 3y x x cắt trục Ox tại mấy điểm 
A. 1 B. 3 C. 2 D. 4 
0027: Hàm số: 3 2 33 3y x mx m Có hai điểm cực trị thì: 
A. 0m B. 0m C. 0m D. 0m 
0028: Giá trị lớn nhất và nhỏ nhất của hàm số 3 23 9 35y x x x trên đoạn [ 4;4] là 
A. 
4;4 4;4
max 40; min 15y y B. 
4;4 4;4
max 40; min 8y y 
C. 
4;4 4;4
max 15; min 1y y D. 
4;4 4;4
max 40; min 41y y 
0029: Cho hàm số 3 23y x x ( )C . Tiếp tuyến với đồ thị ( )C và song song với đường thẳng 9 5y x có 
phương trình là 
A. 9 27y x B. 9 27y x C. 9 2y x D. 9 2y x 
0030: Cho hàm số: 
3 22 3
3
m
y x x m x m . Hàm số luôn đồng biến khi đó m nhận giá trị là: 
A. 2m B. 0m C. 1m D. 4m 
0031: Cho hàm số: 
3 22 1y x x m x ( )C . Đồ thị ( )C tại trục Ox tại 3 điểm phân biệt khi 
A. ;0 \ 1m B. 0; 1m C. ;0m D. 1; \ 0m 
0032: Cho hàm số: 
3 23 2 3y mx x m x . Hàm số nghịch biến trên khi 
A. 1m B. 1m C. 1m D. 1m 
0033: Cho hàm số: 
3 2
2
x
y
x
 ( )C . Đường thẳng 1y x m cắt đồ thị ( )C tại hai điểm phân biệt khi 
A. ;3 5;m B. 3;5m 
C. ;2 10;m D. 2;10m 
0034: Cho hàm số:
3 2 23 3 1y x mx m x hàm số đạt cực đại tại 
0
1x khi m bằng: 
A. 0m B. 2m C. 0 và 2m m D. 0; 2m m 
0035: Cho hàm số 
2 3 2y x x ( )C . Tiếp tuyến với đồ thị ( )C và vuông góc với đường thẳng 1y x 
có phương trình là: 
A. 1y x B. 1y x C. 2 1y x D. 2 1y x 
0036: Hàm số 
3 21 1 3
3
y x m x m x đồng biến trên khoảng 0;3 thì: 
A. 
12
;
7
m B. 
12
;3
7
m C. 
12
;
7
m D. 
12
;3
7
m 
0037: Đồ thị hàm số 
4 2 22 1y x m x m có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác vuông khi: 
A. 0m B. 1m C. 2m D. 3m 
0038: Cho hàm số: 
2 1
1
x
y
x
 ( )C . Đường thẳng 2y x m cắt đồ thị ( )C tại hai điểm phân biệt ,A B 
biết diện tích tam giác OAB bằng 3 khi đó: 
A. 1m B. 2m C. 3m D. 4m 
0039: Cho hàm số 3 2 3 1y x x x , mệnh đề nào sau đây là đúng 
A. Hàm số luôn nghịch biến; B. Hàm số luôn đồng biến 
C. Hàm số đạt cực đại tại 1x D. Hàm số đạt cực tiểu tại 1x 
0040: Hàm số 4 22 1y x x đồng biến trên những khoảng nào ? 
A. 1;0 . B. 1;0 và 1; . C. 1; . D. ; . 
0041: Kết luận nào sau đây về tính đơn điệu của hàm số 
2 1
1
x
y
x
 là đúng 
A. Hàm số luôn nghịch biến trên \{ 1} 
B. Hàm số luôn đồng biến trên \{ 1} 
C. Hàm số luôn nghịch biến trên các khoảng ( ; 1);( 1; ) 
D. Hàm số luôn đồng biến trên các khoảng ( ; 1);( 1; ) 
0042: Hàm số nào sau đây đồng biến trên R? 
A. 
2 2(x 1) 3 2y x B. 
2 1
x
y
x
 C. 
1
x
y
x
 D. tany x 
0043: Hàm số 
1
y x
x
. Mệnh đề nào sau đây là đúng: 
A. Hàm số đồng biến trên từng khoảng xác định ( ;0)và (0; ) 
B. Hàm số nghịch biến trên từng khoảng xác định ( ;0)và (0; ) 
C. Hàm số đồng biến trên ( ; 1)và(1; ) nghịch biến trên( 1;1) 
D. Hàm số nghịch biến trên ( ; 1)và(1; ) đồng biến trên( 1;1) 
0044: Hàm số 
3 23 6y x mx mx m luôn đồng biến khi: 
A. 0 2m B. 0m hoặc 2m C. 0 8m D. 0 8m 
0045: Các điểm cực đại của hàm số: 
3 26 15 1y x x x là : 
A. 5x . B. 1x . C. 1x . D. 5x . 
0046: Hàm số: 
4 22 1y x x có điểm cực tiểu là : 
A. 0x . B. 1x . C. 1x . D. 1, 1x x . 
0047: Cho hàm số 
3 2 2 5
3
y x mx m x . Tìm m để hàm số có cực trị tại x = 1 
A. 1m . B. 
3
4
m . C. 
7
3
m . D. 
4
3
m . 
0048: Cho hàm số 
4 2 5y x mx . Giá trị của m để hàm số có ba cực trị là: 
A. 0m . B. 2m . C. 0m . D. 2m . 
0049: Giá trị nhỏ nhất của hàm số 
2 310 15 6y x x x trên [ 3;3] là: 
A. 35 B. 17 C. 10 D. 2 
0050: Giá trị lớn nhất của hàm số : 
1
1
x
y
x
 trên [2;3] là: 
A. 1 . B. 
1
2
 . C. 2. D. 1 . 
0051: Giá trị nhỏ nhất của hàm số : 3 23 18y x x x trên [0; ) là: 
A. 1 . B. 0. C. 2. D. 1 . 
0052: Cho hình chữ nhật có chu vi bằng 16 cm. Hình chữ nhật đó có diện tích lớn nhất bằng: 
A. 
236cm . B. 220cm . C. 216cm . D. 230cm . 
0053: Tiệm cận đứng của đồ thị hàm số 
2 1
5 3
x
y
x
 là đường thẳng có phương trình: 
A. 
3
5
x B. 
2
5
y C. 
3
5
y D. 
2
5
x 
0054: Tiệm cận ngang của đồ thị hàm số 
6 3
2
x
y
x
 là đường thẳng có phương trình: 
A. 3y B. 2x C. 3x D. 2y 
0055: Với giá trị nào của m thì đồ thị hàm số 
2 1 1m x
y
x m
 có tiệm cận ngang là đường thẳng có phương 
trình 3y ? 
A. 2 B. 1 C. 3 D. 1 
0056: Phương trình tiếp tuyến của đồ thị hàm số 
3 2
1
x
y
x
 tại điểm (2;4)A là 
A. 6y x B. 2y x C. 4y x D. 2 1y x 
0057: Cho hàm số 
2 2 3y x x có đồ thị ( )C . Tiếp tuyến của ( )C tại ( ; )M a b có hệ số góc bằng 2 thì a b 
bằng 
A. 5 B. 4 C. 3 D. 2 
0058: Số giao điểm của đồ thị của hàm số 
4 22 3y x x và trục hoành là 
A. 2 B. 4 C. 1 D. 3 
0059: Với giá trị nào của m thì đồ thị của hàm số 4 22 1y x x và đường thẳng : 1d y m có ít nhất 3 
điểm chung? 
A. 1 0m B. 1 0m C. 0 1m D. 1 0m 
0060: Cho hàm số 
2 3
2
x
y
x
 có đồ thị (C) và đường thẳng d: y = x + m. Với giá trị nào của m thì d cắt (C) tại 
hai điểm phân biệt? 
A. 2m B. 6m C. 2 6m D. 2m hoặc 6m 
0061: Đồ thị được vẽ trên hình là đồ thị 
của hàm số nào dưới đây 
A. 
4 1
2 2
x
y
x
 B. 
2 2
1
x
y
x
 C. 
2 1
1
x
y
x
 D. 
2 1
1
x
y
x
0062: Cho hàm số 3 3 1y x x có đồ thị (C). Với giá trị nào của a thì phương trình: 
3 33 1 3 1x x a a có một nghiệm đơn duy nhất. 
A. 2a B. 2a hoặc 2a C. 0a D. 1a hoặc 1a 
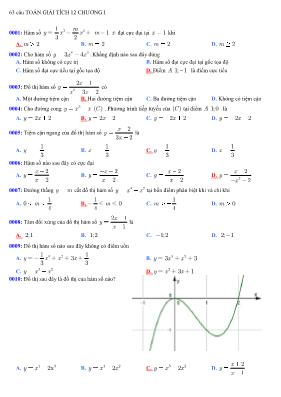
0063: Đồ thị được vẽ trên hình là đồ thị 
của hàm số nào dưới đây 
A. 
3 2y x B. 3 2y x C. 3
1
2 1
3
y x x D. 3 2
1
2
3
y x x