Toán - Đường trung bình của tam giác đường trung bình hình thang

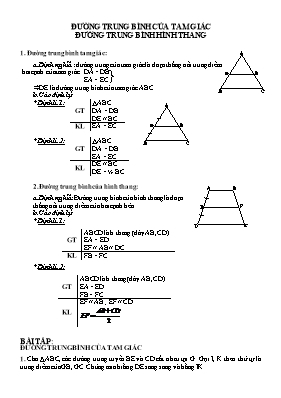
ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC 
ĐƯỜNG TRUNG BÌNH HÌNH THANG
1. Đường trung bình tam giác:
a. Định nghĩa : đường trung của tam giác là đoạn thẳng nối trung điểm
 hai cạnh của tam giác 	DA = DB
EA = EC
ÞDE là đường trung bình của tam giác ABC.
b. Các định lý: 
GT
 ABC
DA = DB
DE // BC
KL
EA = EC
* Định lí 1:
GT
 ABC
DA = DB
EA = EC 
KL
DE // BC
DE = ½ BC
* Định lí 2:
2. Đường trung bình của hình thang:
a. Định nghĩa: Đường trung bình của hình thang là đoạn 
thẳng nối trung điểm của hai cạnh bên.
b. Các định lý: 
* Định lí 1:
GT
ABCD là h.thang (đáy AB, CD)
EA = ED
EF // AB // DC
KL
FB = FC
* Định lí 2:
GT
ABCD là h.thang (đáy AB, CD)
EA = ED
FB = FC 
KL
EF // AB ; EF // CD
BÀI TẬP:
ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC 
1. Cho ABC, các đường trung tuyến BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE song song và bằng IK.
2. Cho ABC, đường trung tuyến AM.
a. Lấy điểm D thuộc AC sao cho DC = 2AD, gọi I là giao điểm của BD và AM. Chứng minh rằng AI = MI.
b. Gọi I là trung điểm của AM, D là giao điểm của BI và AC. Chứng minh rằng DC = 2AD.
3. Cho tam giác ABC vuông tại B, Â = 600, phân giác AD. Gọi M,N, I theo thứ tự là trung điểm của AD, AC, CD.
a. Chứng minh rằng BMNI là hình thang cân.
b. Tính các góc của tứ giác BMNI.
4. Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh rằng MI = IK = KN
5. Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng:
a. EI // CD; IF // AB.
B. EF ≤ 
6. Cho hình thang ABCD (AB // CD), gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng ba điểm E, F, I thẳng hàng.
7. Cho hình thang ABCD (AB // CD), gọi E, F, I theo thứ tự là trung điểm của AD , BC, AC, BD. Tính độ đài các đoạn EK, KI, IF biết:
a. AB = 12cm và CD = 16cm
b. AB = 8cm và CD = 6cm.
ĐƯỜNG TRUNG BÌNH HÌNH THANG
9. Cho hình thang ABCD (AB // CD), gọi E, F, I, K theo thứ tự là trung điểm của AD, BC, AC, BD. Tính độ dài các đoạn EK, KI, IF biết AB = 18cm và CD = 12cm.
10. Cho hình thang vuông ABCD (Â= = 900), gọi M là trung điểm của BC. Chứng minh rằng tam giác MAD là tam giác cân.
11. Cho h.thang ABCD (AB//CD), có AB = a, CD = b. Trên AD lấy 2 diểm E, F sao cho AE = EF = FD, trên BC lấy hai điểm M, N, sao cho BM = MN = NC. Tính độ dài các đoạn EM, FN theo a và b.
12. Cho h.thang ABCD (AB//CD), có AB = a, BC = b, CD = c, DA = d. Các đường phân giác của các góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N
a. Chứng minh rằng MN//AB
b. Tính độ dài MN theo a, b, c, d
13. Đường cao xuất phát từ đỉnh góc tù của một hình thang cân chia đáy lớn thành hai đoạn thẳng có độ dài 6cm và 30cm. Tính độ dài đường trung bình của hình thang đó.