Toán 12 - Chương III: Phương pháp tọa độ trong không gian

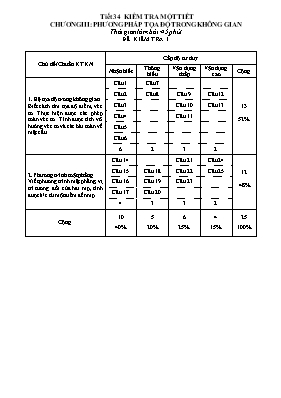
 Tiết 34 KIỂM TRA MỘT TIẾT 
CHƯƠNG III: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Thời gian làm bài: 45 phút
ĐỀ KIỂM TRA 1
Chủ đề/Chuẩn KTKN
Cấp độ tư duy
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Cộng
1. Hệ tọa độ trong không gian
Biết cách tìm tọa độ điểm, véc tơ. Thực hiện được các phép toán véc tơ. Tính được tích vô hướng véc tơ và các bài toán về mặt cầu.
Câu 1
Câu 7
13
52%
Câu 2
Câu 8
Câu 9
Câu 12
Câu 3
Câu 10
Câu 13
Câu 4
Câu 11
Câu 5
Câu 6
6
2
3
2
2. Phương trình mặt phẳng
Viết phương trình mặt phẳng, vị trí tương đối của hai mp, tính được k/c từ một điểm đến mp. 
Câu 14
Câu 21
Câu 24
12
 48%
Câu 15
Câu 18
Câu 22
Câu 25
Câu 16
Câu 19
Câu 23
Câu 17
Câu 20
4
3
3
2
Cộng
10
40%
5
20%
6
25%
4
15%
25
100%
BẢNG MÔ TẢ CHI TIẾT NỘI DUNG CÂU HỎI ĐỀ KIỂM TRA
CHƯƠNG III: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
ĐỀ KIỂM TRA 1
Chủ đề
Câu
Nội dung
1. Hệ tọa độ trong không gian
Biết cách tìm tọa độ điểm, véc tơ. Thực hiện được các phép toán véc tơ. Tính được tích vô hướng véc tơ và các bài toán về mặt cầu.
1
Nhận biết: CT tính tọa độ trung điểm của đoạn thẳng
2
Nhận biết: CT tính khoảng cách giữa hai điểm
3
Nhận biết: Cách biểu diễn một vecto qua các vecto đơn vị
4
Nhận biết : 2 vecto bằng nhau
5
Nhận biết: Viết phương trình mặt cầu
6
Nhận biết: độ dài vecto và điều kiện 2 vecto vuông góc
7
Thông hiểu: Cộng, trừ vecto, nhân vecto với một số và hai vecto bằng nhau
8
Thông hiểu: Điều kiện để 2 vecto cùng phương, 3 điểm thẳng hàng
9
Vận dụng thấp: Cho tọa độ ba điểm A,B,C. Tìm D để ABCD là hình bình hành.
10
Vận dụng thấp: Cho Tam giác ABC biết tọa độ A,B,C. Tính độ dài đoạn thẳng từ một đỉnh đến trọng tâm của tam giác.
11
Vận dụng thấp: Viết phương trình mặt cầu biết đường kính AB với A,B có tọa độ cho trước.
12
Vận dụng cao: Cho hai điểm A,B. Tìm điểm C trên một trục tọa độ sao cho tam giác ABC là tam giác vuông.
13
Vận dụng cao: Viết phương trình mặt cầu đi qua hai điểm A,B và có tâm nằm trên một trục tọa độ.
2. Phương trình mặt phẳng
Viết phương trình mặt phẳng, vị trí tương đối của hai mp, tính được k/c từ một điểm đến mp.
14
Nhận biết: Kiểm tra một điểm có thuộc thuộc mặt phẳng hay không.
15
Nhận biết: Xác định VTPT của mp
16
Nhận biết: Lập phương trình mp theo đoạn chắn biết tọa độ 3 điểm.
17
Nhận biết: Lập PTMP biết một điểm và song song với đường thẳng cho trước
18
Thông hiểu: Lập PTMP biết một điểm và vuông góc với đường thẳng cho trước
19
Thông hiểu: Xác định phương trình mp chứa một trục tọa độ cho trước.
20
Vận dụng thấp: Lập phương trình mp đi qua ba điểm cho trước.
21
Vận dụng thấp: viết được phương trình mặt phẳng dựa vào tích có hướng để tìm được véc tơ pháp tuyến
22
Vận dụng thấp: Vận dụng được phương trình mặt phẳng theo đoạn chắn để viết phương trình mặt phẳng
23
Vận dụng thấp: Viết phương trình mặt phẳng biết vectơ pháp tuyến
24
Vận dụng cao: Tìm điểm thuộc mặt phẳng thông qua bài toán cực trị
25
Vận dụng cao: Cho điểm M và mp (P). Mp(Q) song song với (P) và cách đều (P), (Q). Viết phương trình mp (Q).
363
ĐỀ KIỂM TRA 1
Câu 1.Trong không gian với hệ tọa độ (Oxyz). Cho 2 điểm A(2;2;-3), B(4;0;1).
Khi đó tọa độ trung điểm I của đoạn thẳng AB là.
A. I(-1;1;2). B. I(3;-1;-1). C. I(3;1;-1). D. I(1;-1;2).
Câu 2. Trong không gian với hệ tọa độ (Oxyz). Cho 2 điểm A(1;1;1), B(1;0;1).
Khoảng cách giữa hai điểm A, B là bao nhiêu?
A. AB = 4. B. AB = 3. C. AB = 2. D. AB = 1.
Câu 3. Trong không gian với hệ tọa độ (Oxyz). Cho vecto: .
Khẳng định nào sau đây là đúng?
A. B. C. D. 
Câu 4. Trong không gian Oxyz, cho 2 vecto và . Nếu thì x bằng
A.1	B. -1	C. -2	D. 2
Câu 5. Trong không gian Oxyz, mặt cầu (S) có tâm I(1;2;-3) và đi qua A(1;0;4) có phương trình
A. 	B. 
C. 	D. 
Câu 6. Trong không gian Oxyz, cho 3 vecto ; ; . Trong các mệnh đề sau, mệnh đề nào sai
A. 	 B.	C. 	D. 
Câu 7. Trong không gian với hệ tọa độ (Oxyz). Cho hai vecto , và . Tìm tọa độ điểm M thỏa mãn .
A. B. C. D. 
Câu 8. Trong không gian với hệ tọa độ (Oxyz). Cho bốn điểm ; ; ; . Bộ ba điểm nào sau đây thẳng hàng?
A. M,N,P. B. M,N,Q. C. M,P,Q. D. N,P,Q.
Câu 9. Trong không gian với hệ tọa độ (Oxyz). Cho A(1; 2; 3), B(2; -1; 1), C(1; 1; -2). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
A. D(0; 4; 0).	 B. D(2; -2; -4).	 C. D(2; 0; 6).	 D. D(2; -2; -4).
Câu 10. Trong không gian với hệ tọa độ (Oxyz). Cho tam giác ABC có trọng tâm G, biết 
A(-1; -2; -3), B(-2; -3; -1), C(-3; -1; -2). Tính độ dài AG?
A. 	 B. 	 C. 	 D. 
Câu 11. Phương trình mặt cầu đường kính AB biết A(2; -4; 6), B(4; 2; -2) là?
A. B. 
C. D. .
Câu 12. Trong không gian với hệ tọa độ (Oxyz). Cho A(2; -2; 3), B(1; -1; 2). Tìm tọa độ điểm C nằm trên trục Oy sao cho tam giác ABC vuông tại A?
A. C(0; -7; 0).	 B. C(0; -3; 0).	 C. C(3; 0; 0).	 D. C(0; 0; 3).
Câu 13. Phương trình mặt cầu đi qua hai điểm A(1; 3; 0) và B(4; 0; 0) biết tâm mặt cầu nằm trên Ox là?
A. B. 
C. D. 
Câu 14. Điểm M thuộc mặt phẳng (P): có tọa độ là 
A. M	B. M	C. M	D. M
Câu 15. Một véctơ pháp tuyến của mặt phẳng (Q) có tọa độ là
Câu 16. Gọi là mặt phẳng cắt ba trục tọa độ tại 3 điểm M (8; 0; 0), N(0; -2; 0) , P(0; 0; 4). Phương trình của mặt phẳng là?
	 C. x – 4y + 2z = 0.	 D. x – 4y + 2z – 8 = 0.
Câu 17. Phương trình mặt phẳng (P) đi qua điểm A(2;3;4) và song song với mặt phẳng (Q) : là 
Câu 18. Phương trình mặt phẳng (P) đi qua điểm A(2;3;4) và vuông góc với trục Ox là ?
Câu 19. Mặt phẳng nào sau đây chứa trục Oy ?
A. -2x – y = 0.	B. -2x + z =0.	C. –y + z = 0.	D. -2x – y + z =0.
Câu 20. Cho 3 điểm A(0; 2; 1), B(3; 0; 1), C(1; 0; 0). Phương trình mặt phẳng (ABC) là ?
A. 2x – 3y – 4z + 10 = 0.	B. 4x + 6y – 8z + 2 = 0.
C. 2x + 3y – 4z – 2 = 0.	D. 2x – 3y – 4z + 1 = 0.
Câu 21. Trong không gian Oxyz, cho mặt phẳng (P) đi qua hai điểm A(4,-1,1), B(3,1,-1) và song song với trục Ox. Phương trình nào sau đây là phương trình của mặt phẳng (P):
 	A. 	B. 	C. 	D. 
Câu 22. Trong không gian Oxyz, cho điểm M(8,-2,4). Gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy, Oz. Phương trình mặt phẳng đi qua ba điểm A, B và C là:
A. 	B. 
C. 	D. 
Câu 23. Các mặt phẳng (Q) song song với mp(P): x+2y+z-4=0 và cách D(1;0;3) một khoảng bằng có phương trình là:
x+2y+z+2=0. 	B. x+2y-z-10=0.	
C. x+2y-z+10=0. 	D. x+2y+z+2=0 và x+2y+z-10=0.
Câu 24. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4) và mặt phẳng (P): 2x + y – z + 6 =0. Tọa độ điểm M nằm trên (P) sao cho MA2 + MB2 nhỏ nhất là
A. M(-1;1;5).	B. M(1;-1;3).	 C. M(2;1;-5).	D. 
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng và điểm . Mặt phẳng (Q) song song với mặt phẳng (P) và khoảng cách từ M đến (P) và (Q) là bằng nhau thì (Q) có phương trình là
A. 	B. 	C. 	 D. Đáp án khác.
Ngày 11 Tháng 3 Năm 2017
Duyệt của TTCM
Thân Văn Trung
Tiết 34 KIỂM TRA MỘT TIẾT 
CHƯƠNG III: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Thời gian làm bài: 45 phút
ĐỀ KIỂM TRA 2
Chủ đề/Chuẩn KTKN
Cấp độ tư duy
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Cộng
1. Hệ tọa độ trong không gian
Biết cách tìm tọa độ điểm, véc tơ. Thực hiện được các phép toán véc tơ. Tính được tích vô hướng véc tơ và các bài toán về mặt cầu.
Câu 1
Câu 7
13
52%
Câu 2
Câu 8
Câu 9
Câu 12
Câu 3
Câu 10
Câu 13
Câu 4
Câu 11
Câu 5
Câu 6
6
2
3
2
2. Phương trình mặt phẳng
Viết phương trình mặt phẳng, vị trí tương đối của hai mp, tính được k/c từ một điểm đến mp. 
Câu 14
Câu 21
Câu 24
12
 48%
Câu 15
Câu 18
Câu 22
Câu 25
Câu 16
Câu 19
Câu 23
Câu 17
Câu 20
4
3
3
2
Cộng
10
40%
5
20%
6
25%
4
15%
25
100%
BẢNG MÔ TẢ CHI TIẾT NỘI DUNG CÂU HỎI ĐỀ KIỂM TRA
CHƯƠNG III: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
ĐỀ KIỂM TRA 2
Chủ đề
Câu
Nội dung
1. Hệ tọa độ trong không gian
Biết cách tìm tọa độ điểm, véc tơ. Thực hiện được các phép toán véc tơ. Tính được tích vô hướng véc tơ và các bài toán về mặt cầu.
1
Nhận biết: CT tính tọa độ trọng tâm của một tam giác
2
Nhận biết: CT tính khoảng cách giữa hai điểm
3
Nhận biết: Viết phương trình mặt cầu
4
Nhận biết : Tọa độ của một vecto
5
Nhận biết: Tọa độ trung điểm đoạn thẳng
6
Nhận biết: Tìm tâm và bk mặt cầu
7
Thông hiểu: Viết pt mặt cầu
8
Thông hiểu: Cộng vecto, nhân vecto với một số 
9
Vận dụng thấp: Tọa độ điểm
10
Vận dụng thấp: Ứng dụng của vecto
11
Vận dụng thấp: Kiến thức liên quan tới mặt cầu.
12
Vận dụng cao: Tìm tọa độ điểm để độ dài lớn nhất
13
Vận dụng cao: PT mặt cầu đi qua 4 điểm
2. Phương trình mặt phẳng
Viết phương trình mặt phẳng, vị trí tương đối của hai mp, tính được k/c từ một điểm đến mp.
14
Nhận biết: Pt mặt phẳng theo đoạn chắn.
15
Nhận biết: Xác định VTPT của mp
16
Nhận biết: Lập phương trình mp trung trực của đoạn thẳng
17
Nhận biết: Khoảng cách từ 1 điểm tới 1 mp
18
Thông hiểu: Lập PTMP biết một điểm và song song với MP cho trước
19
Thông hiểu: Độ dài đoạn thẳng
20
Vận dụng thấp: Lập phương trình mp đi qua ba điểm cho trước.
21
Vận dụng thấp: Tìm tọa độ điểm thứ 4 để là hbh
22
Vận dụng thấp: Viết phương trình tiếp xúc với 1 mặt phẳng
23
Vận dụng thấp: Viết phương trình mặt phẳng đi qua 2 điểm và vuông góc vơi 1 mp
24
Vận dụng cao: Tính thể tích tứ diện
25
Vận dụng cao: Cho điểm A và mp (P). Mp(Q) song song với (P) và cách đều (P), (Q). Viết phương trình mp (Q).
363
ĐỀ KIỂM TRA 2
Câu 1. Trong không gian Oxyz. Cho ba điểm A(1;1;3); B(-1; 3; 2); C(-1;2;3 ). Tọa độ trọng tâm G của tam giác ABC là.
 A. G(0; 0; 6); B. G(0;3/2;3); C. G(-1/3;2; 8/3) D. G(0;3/2;2); 
Câu 2. Trong không gian Oxyz, khoảng cách giữa hai điểm A(2;3;4) và B(6;0;4) bằng :
A. 	B. 	C. 5	D. 
Câu 3. Trong không gian Oxyz, phương trình mặt cầu tâm I(2;1;-2) bán kính R=2 là:
A. 	B. 
C. 	D. 
Câu 4. Trong không gian Oxyz, cho . Khi đó tọa độ của là:
A. 	B. 	C. 	D. 
Câu 5. Cho ba điểm A(1;1;3); C(-1;2;3). Tọa độ trung điểm I của đoạn AC là
 A. I(0; 0; 6); B. I(0;3/2;3); C. I (-1/3;2; 8/3) D. I(0;3/2;2); 
Câu 6. Cho mặt cầu (S) tâm I bán kính R và có phương trình:	 Trong các mệnh đề sau, mệnh đề nào đúng
A. và R= B. và R=	
C. và R= D. và R=	
Câu 7. Phương trình mặt cầu (S) qua điểm A( 1;2; 0) và có tâm là gốc tọa độ O là.
 A. 2 B. 
C. D. 
Câu 8. Cho ba véc tơ . Tọa độ véc tơ là
 A. B. (13 ;1;3); C. (-1; -7; 2); D. (-1;28;3)
Câu 9. Trong không gian Oxyz, cho vecto . Tọa độ của điểm A là
	A. 	B. 	C. 	D. 
Câu 10. Trong không gian Oxyz, cho 3 vecto ; ; . Trong các mệnh đề sau, mệnh đề nào đúng?
A. 	B. đồng phẳng	
C. 	D. 
Câu 11. Trong không gian Oxyz, cho mặt cầu (S): . Trong các mệnh đề sau, mệnh đề nào sai:
A. S có tâm I(-1;2;3)	B. S có bán kính 
C. S đi qua điểm M(1;0;1)	 D. S đi qua điểm N(-3;4;2)	
Câu 12. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4). Tọa độ điểm M nằm trên trục Ox sao cho MA2 + MB2 lớn nhất là: 
	A. M(0;0;0)	B. M(0;3;0)	C. M(3;0;0)	D. M(-3;0;0)
Câu 13. Trong không gian Oxyz, bán kính mặt cầu đi qua bốn điểm A(1;0;0), B(0;1;0), C(0;0;1) và D(1;1;1) là: 
A. 	B. 	C. 	D. 
Câu 14. Trong không gian Oxyz. Cho bốn điểm A(1; 0; 0); B(0; 3; 0); C(0; 0; 6). Phương trình mặt phẳng (ABC) là.
 A. B. x+2y+z-6 = 0 C. D. 6x+2y+z-3 = 0
Câu 15. Cho mặt phẳng (P): Khẳng định nào sau đay SAI?
A. VTPT của mặt phẳng (P) là 
B. Mặt phẳng (P) song song với Oz
C. Điểm M(-2;0;0) thuộc (P)
D. Mặt phẳng (P) song song với mặt phẳng (Oxy)
Câu 16. Trong không gian Oxyz, cho 2 điểm A(4;-1;3), B(-2;3;1). Phương trình mặt phẳng trung trực của đoạn AB là:
A. 	 B. C. 	 D. 
Câu 17. Cho điểm A (-1; 3; - 2) và mặt phẳng . Khoảng cách từ A đến (P) là.
A. . 	B. . 	 C. . 	D. . 
Câu 18. Phương trình mp(a) đi qua điểm M(1,-1,2) và song song với mp:2x-y+3z -1 = 0 là
 A. 6x + 3y + 2z – 6 = 0 B. x + y + 2z – 9= 0 C. 2x-y+3z-9= 0 
D. 3x + 3y - z – 9 = 0 
Câu 19. Trong không gian Oxyz. Cho A( 4; 2; 6); B(10; - 2; 4), C(4; - 4; 0); D( - 2; 0; 2) thì tứ giác ABCD là: hình 
A. Thoi B. Bình hành C. Chữ nhật D. Vuông
Câu 20. Trong kh«ng gian Oxyz, cho B(0 ; -2 ; 1) ; C(1 ; -1 ; 4) ; D (3; 5 ; 2). Ph­¬ng tr×nh mÆt ph¼ng (BCD) là.
A. -5x+2y+z+3=0 B. 5x+2y+z+3=0 . C. -5x+2y+z-3=0 D. -5x+2y-z+3=0 
Câu 21. Trong kh«ng gian Oxyz. Cho 3 điểm M(2;1;3), N(4;0;-1); P(-2;3;1). Nếu MNPQ là hình bình hành thì tọa độ điểm Q là:
A. (0;-2;3)	B. (0;-2;-3)	C. (0;2;-3)	D. (-4;4;5)
Câu 22. Trong kh«ng gian Oxyz, cho A(3 ; -2 ;- 2) ; B(3 ; 2 ; 0) ; C(0 ; 2 ; 1) ; D (-1; 1 ; 2) . Ph­¬ng tr×nh mÆt cÇu t©m A tiÕp xóc víi mÆt ph¼ng (BCD) là.
A. B. 
C. D. 
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1),B(–1;1;3) và mặt phẳng (P): .Phương trình mặt phẳng (Q) đi qua hai điểm A,B và vuông góc với mặt phẳng (P) là.
A. 	 B. 
C. 	 D. 
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A(1;0;0), B(2;1;1), C(0;3;-2), D(1;3;0). Thể tích tứ diện đã cho là
A. 1 B. C. D. 6
Câu 25. Cho mặt phẳng (P): 2x –y +2z –3 =0. Phương trình của mặt phẳng (Q) song song với mặt phẳng (P) biết (Q) cách điểm A(1;2;3) một khoảng bằng 5 là.
    A. (Q): 2x –y +2z +9=0     B. (Q): 2x –y +2z + 15 =0
    C. (Q): 2x –y +2z – 21=0  D. Cả A, C đều đúng.