Tiết 46: Kiểm tra chương II - Hình học 7

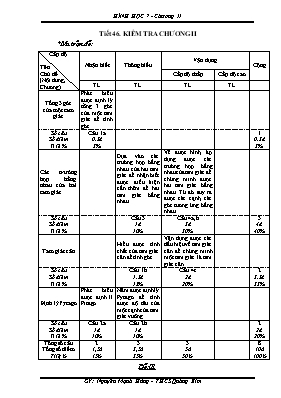
Tiết 46. KIỂM TRA CHƯƠNG II 
	*Ma trận đề: 
Cấp độ
Tên
Chủ đề
(Nội dung,
Chương)
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TL
TL
TL
TL
Tổng 3 góc của một tam giác
Phát biểu được định lý tổng 3 góc của một tam giác để tính góc
Số câu
Số điểm
Tỉ lệ %
Câu 1a
0,5đ
5%
1
0,5 đ
5%
Các trường hợp bằng nhau của hai tam giác
Dựa vào các trường hợp bằng nhau của hai tam giác để nhận biết được điều kiện cần thêm để hai tam giác bằng nhau.
Vẽ được hình, áp dụng được các trường hợp bằng nhau của tam giác để chứng minh được hai tam giác bằng nhau. Từ đó suy ra được các cạnh, các góc tương ứng bằng nhau
Số câu
Số điểm
Tỉ lệ %
Câu 3
1đ
10%
Câu 4a,b
3đ
30%
3
4đ
40%
Tam giác cân
Hiểu được tính chất của tam giác cân để tính góc
Vận dụng được các dấu hiệu về tam giác cân để chứng minh một tam giác là tam giác cân
Số câu
Số điểm
Tỉ lệ %
Câu 1b
1,5đ
15%
Câu 4c
2đ
20%
2
3,5đ
35%
Định lý Pytago
Phát biểu được định lí Pitago
Nắm được định lý Pytago để tính được độ dài của một cạnh của tam giác vuông
Số câu
Số điểm
Tỉ lệ %
Câu 2a
1đ
10%
Câu 2b
1đ
10%
2
2đ
20%
Tổng số câu
Tổng số điểm
Tỉ lệ %
2
1,5đ
15%
3
3,5đ
35%
3
5đ
50%
8
10đ 100%
Đề:01
Câu 1. (2.5 điểm)
	 a) Phát biểu định lí về tổng ba góc của một tam giác?
	 b) Áp dụng: MNP cân tại P. Biết góc N có số đo bằng 500. Tìm số đo góc P?
Câu 2. (2.5 điểm)
	a) Phát biểu định lí Pytago?
	b) Áp dụng: HIK vuông tại H có các cạnh góc vuông là 3cm; 4cm. Độ dài cạnh huyền IK bằng bao nhiêu?
Câu 4. (5 điểm)
	Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H BC)
	a) Chứng minh HB = HC 
	b) Chứng minh 
	c) Kẻ HD vuông góc với AB (D AB). Kẻ HE vuông góc với AC (E AC). Chứng minh tam giác HDE là tam giác cân.
Đề 02:
Câu 1: (2.5 điểm)
a. Phát biểu định lý Pytago đảo ?
b. Kiểm tra xem tam giác có ba cạnh lần lượt là 12 cm, 13 cm, 5 cm có phải là độ dài 3 cạnh của tam giác vuông hay không?
Câu 2: Tam giác ABC vuông tại B. 
a. Độ dài hai cạnh góc vuông là AB, BC lần lượt là: . Tính độ dài AC ?
b. Cạnh huyền AC là 5 cm và cạnh BC là 4 cm. Tính độ dài cạnh AB ?
Câu 3: Câu 4. (5 điểm)
	Cho tam giác MNP cân tại M. Kẻ MH vuông góc với NP (H NP)
	a) Chứng minh HP = HN 
	b) Chứng minh 
	c) Kẻ HD vuông góc với AB (D AB). Kẻ HE vuông góc với AC (E AC). Chứng minh tam giác HDE là tam giác cân.
3. Đáp án - biểu điểm
Câu 1. (2.5 điểm)
	 a) Tổng ba góc của một tam giác bằng 1800 (0,5đ)
	 b) Áp dụng: 
	VìMNP cân tại P nên= 500 (theo t/c của tam giác cân) (0,25đ)
	 Mà (định lí tổng ba góc của 1 tam giác) (0,5đ)
	Suy ra (0,5đ)
 	Vậy = 800 (0,25đ)
Câu 2. (2.5 điểm)
	a) Định lí Pitago: Trong một tam giác vuông bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông. (1đ)
	b) Áp dụng: 
	VìHIK vuông tại H có các cạnh góc vuông là 3cm; 4cm. (0,25đ)
	Khi đó IK2 = HI2 + HK2 = 32 + 42 = 25 (0,5đ)
	Vậy IK = (cm) (0,25đ)
Câu 3. (1 điểm)
	Ta có ABC và DEF có AB = DE, BC = EF. Vì vậy cần thêm điều kiện AC = DF thì ABC = DEF theo trường hợp cạnh - cạnh - cạnh 
Câu 4. (5điểm)
	Vẽ hình đúng, sạch sẽ (0,5đ)
Ghi GT, KL đầy đủ, chính xác (0,5đ)
GT
A
D
C
E
B
H
ABC, AB = AC
 AH BC (H C)
 HD AB (D AB)
 HE AC (E AC)
KL
a) HB = HC
b) 
c) HDE cân
Chứng minh
	a) Xét AHB và AHC có: 
 (1đ) 
 Từ đó, suy ra HB = HC (2 cạnh tương ứng) (0,5đ)
b) Vì AHB = AHC (c/m trên) 
	 Nên suy ra (2 góc tương ứng) (0,5đ) 
c) Xét HDB và HEC có: 
 (1đ) 	Do đó HD = HE (2 cạnh tương ứng) (0,5đ)
Vậy HDE có HD = HE nên là tam giác cân (theo định nghĩa tam giác cân) (0,5đ)