Tài liệu bài giảng: Các vấn đề về khoảng cách (phần 01)

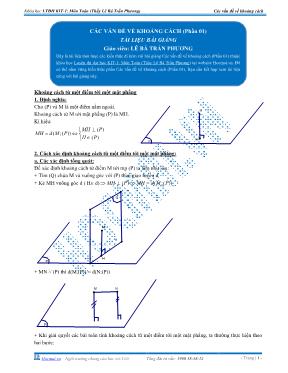
Khĩa học LTðH KIT-1: Mơn Tốn (Thầy Lê Bá Trần Phương) Các vấn đề về khoảng cách 
 Hocmai.vn – Ngơi trường chung của học trị Việt Tổng đài tư vấn: 1900 58-58-12 - Trang | 1 -
P
M
H
Khoảng cách từ một điểm tới một mặt phẳng 
1. ðịnh nghĩa: 
Cho (P) và M là một điểm nằm ngồi. 
Khoảng cách từ M tới mặt phẳng (P) là MH. 
Kí hiệu: 
( )
( ;( ))
( )
MH P
MH d M P
H P
⊥
= ⇔ 
∈
2. Cách xác định khoảng cách từ một điểm tới một mặt phẳng: 
a. Các xác định tổng quát: 
ðể xác định khoảng cách từ điểm M tới mp (P) ta làm như sau: 
+ Tìm (Q) chứa M và vuơng gĩc với (P) theo giao tuyến d. 
+ Kẻ MH vuơng gĩc d ( H∈d) ( ) ( ; ( ))MH P MH d M P⇒ ⊥ ⇒ = 
P
d
Q
M
H
+ MN // (P) thì d(M,(P)) = d(N;(P)) 
P
M N
+ Khi giải quyết các bài tốn tính khoảng cách từ một điểm tới một mặt phẳng, ta thường thực hiện theo 
hai bước: 
CÁC VẤN ðỀ VỀ KHOẢNG CÁCH (Phần 01) 
TÀI LIỆU BÀI GIẢNG 
Giáo viên: LÊ BÁ TRẦN PHƯƠNG 
ðây là tài liệu tĩm lược các kiến thức đi kèm với bài giảng Các vấn đề về khoảng cách (Phần 01) thuộc 
khĩa học Luyện thi đại học KIT-1: Mơn Tốn (Thầy Lê Bá Trần Phương) tại website Hocmai.vn. ðể 
cĩ thể nắm vững kiến thức phần Các vấn đề về khoảng cách (Phần 01), Bạn cần kết hợp xem tài liệu 
cùng với bài giảng này. 
Khĩa học LTðH KIT-1: Mơn Tốn (Thầy Lê Bá Trần Phương) Các vấn đề về khoảng cách 
 Hocmai.vn – Ngơi trường chung của học trị Việt Tổng đài tư vấn: 1900 58-58-12 - Trang | 2 -
A
B
C
H
 * Xác định khoảng cách 
 * Tính khoảng cách. 
+ Các hệ thức cơ bản cần nhớ: 
2 2 2
2
2
2
1 1 1
.
.
.
AH AB AC
AB BH BC
AC CH CB
AH HB HC
= +
=
=
=
Bài 1. Cho chĩp S.ABCD cĩ đáy ABCD là hình vuơng cạnh a. SA vuơng gĩc với mặt phẳng đáy, SA = 
2a. 
a) Tính khoảng cách từ điểm A đến mặt phẳng (SBC). 
b) Tính khoảng cách từ A đến mặt phẳng (SBD). 
Bài 2. Cho chĩp S.ABCD cĩ đáy ABCD là hình vuơng cạnh a, tam giác SAB đều, mặt phẳng (SAB) 
vuơng gĩc với mặt phẳng (ABCD). Gọi I, J là trung điểm của AB và AD. Tính khoảng cách từ I đến mặt 
phẳng (SFC). 
Bài 3. Cho chĩp S.ABCD cĩ SA = a, các cạnh cịn lại bằng 
3
2
a
. Chứng minh rằng SA ⊥ SC và tính d(S, 
(ABCD)). 
Giáo viên: Lê Bá Trần Phương 
 Nguồn: Hocmai.vn