Ngân hàng đề trắc nghiệm Giải tích 12 - Đề số 004 - Hàm số và các vấn đề liên quan

GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ TRẮC NGHIỆM THPT
CHUYÊN ĐỀ : HÀM SỐ VÀ CÁC VẤN ĐỀ LIÊN QUAN
(ĐỀ 004-KSHS)
C©u 1 : 
Giá trị nhỏ nhất của hàm số đạt tại , tìm :
A.
B.
C.
D.
C©u 2 : 
Tìm m để pt sau có nghiệm 
A.
B.
-1<m< 
C.
D.
m>-1
C©u 3 : 
Cho hàm số và ; , . Tìm câu đúng?
A.
M = 13 và m = 4
B.
M = 5 và m = 0
C.
M = 5 và m = 4
D.
M = 13 và m = 5
C©u 4 : 
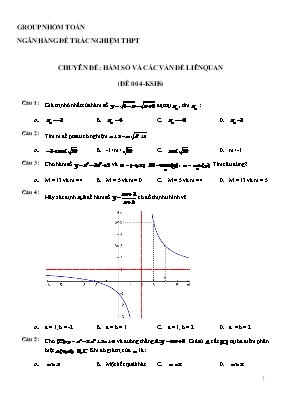
Hãy xác định để hàm số có đồ thị như hình vẽ
A.
a = 1; b = -2
B.
a = b = 1
C.
a = 1; b = 2
D.
a = b = 2
C©u 5 : 
Cho và đường thẳng . Giả sử cắt tại ba điểm phân biệt , . Khi đó giá trị của là:
A.
B.
Một kết quả khác
C.
D.
C©u 6 : 
Cho hàm số . Gọi d là đường thẳng đi qua điểm A(- 1; 0) với hệ số góc là k ( k thuộc R). Tìm k để đường thẳng d cắt (C) tại ba điểm phân biệt và hai giao điểm B, C ( B, C khác A ) cùng với gốc tọa độ O tạo thành một tam giác có diện tích bằng 1.
A.
B.
Đáp án khác
C.
D.
C©u 7 : 
Giá trị lớn nhất của hàm số y=4x3-3x4 là:
A.
3
B.
4
C.
8
D.
6
C©u 8 : 
Đồ thị hàm số cắt trục hoành tại hai điểm M và N thì
A.
B.
C.
D.
C©u 9 : 
Cho hàm số . Mệnh đế nào sau đây sai?
A.
Đồ thị tồn tại một cặp tiếp tuyến vuông góc với nhau
B.
Tại giao điểm của đồ thị và , tiếp tuyến song song với đường thẳng 
C.
Tại , tiếp tuyến của đồ thị có hệ số góc 
D.
Lấy thuộc đồ thị với thì tiếp tuyến tại song song với nhau
C©u 10 : 
Xác định tiệm cận của đồ thị hàm số 
A.
Tiệm cận đứng: ; Tiệm cận ngang: 
B.
Tiệm cận đứng: ; Tiệm cận ngang: 
C.
Tiệm cận đứng: ; Tiệm cận ngang: 
D.
Tiệm cận đứng: ; Tiệm cận ngang: 
C©u 11 : 
Tìm cực trị của hàm số sau 
A.
Điểm CT 
B.
Điểm CT(-1:3)
C.
Không có
D.
Điểm CĐ (1;3)
C©u 12 : 
Cho hàm số (1). Tìm m để đường thẳng d : y = x + 4 cắt đồ thị hàm số (1) tại ba điểm phân biệt A, B, C sao cho tam giác MBC có diện tích bằng 4 . ( Điểm B, C có hoành độ khác không ; M(1;3) ).
A.
B.
C.
D.
C©u 13 : 
Cho hàm số . Tìm m để đường thẳng d : 2x + 2y - 1= 0 cắt tại hai điểm phân biệt A, B sao cho tam giác OAB có diện tích bằng .
A.
B.
C.
D.
C©u 14 : 
Tìm m để hàm số đạt cực đại tại x=-1
A.
B.
m=1
C.
D.
m=-3
C©u 15 : 
Tìm giá trị LN và NN của hàm số 
A.
m=-3
B.
M=-2
C.
m=1;M=2
D.
m=-1;M=5
C©u 16 : 
Cho hàm số . Trên , hàm số có giá trị nhỏ nhất bằng 0. Tính a?
A.
B.
C.
D.
C©u 17 : 
Tìm m để hàm số có ba cực trị.
A.
B.
C.
D.
C©u 18 : 
Cho hàm số có đồ thị (C). Phương trình tiếp tuyến của (C), biết tiếp tuyến cắt trục Ox, Oy lần lượt tại A, B và tam giác OAB cân tại O là :
A.
B.
C.
D.
C©u 19 : 
Cho hàm số , gọi A là điểm cực đại của hàm số trên. A có tọa độ:
A.
A(0,0)
B.
A(2,-2)
C.
A(0,2)
D.
A(-2,-2)
C©u 20 : 
Cho hàm số đạt cực tiểu tại . Kết luận nào sau đây đúng? 
A.
B.
C.
D.
C©u 21 : 
Xác định m để hàm số đạt cực tiểu tại 
A.
B.
C.
D.
C©u 22 : 
Tìm giá trị lớn nhất M của hàm số trên 
A.
B.
C.
D.
C©u 23 : 
Hàm số đạt cực đại tại khi
A.
B.
C.
D.
C©u 24 : 
Với giá trị nào của m thì tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng song song với đường thẳng ?
A.
B.
C.
D.
C©u 25 : 
Cho hàm số . Tìm m để hàm số (1) có cực đại , cực tiểu , đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác vuông tại O.
A.
B.
C.
D.
C©u 26 : 
Cho hàm số (1). Tìm m dể hàm số (1) có ba điểm cực trị là ba đỉnh của một tam giác vuông cân 
A.
B.
C.
D.
C©u 27 : 
Cho hàm số , tìm m để hàm số đồng biến trên từng khoảng xác định.
A.
B.
C.
D.
C©u 28 : 
Tìm m để đường thẳng cắt đồ thị hàm số tại bốn điểm phân biệt.
A.
B.
C.
D.
C©u 29 : 
Cho hàm số . Tìm tọa độ điểm M thuộc (C) , biết tiếp tuyến tại M cắt hai trục Ox, Oy tại hai điểm A, B sao cho tam giác OAB có diện tích bằng . 
A.
B.
C.
D.
C©u 30 : 
Tìm GTNN của hàm số trên [0,1]
A.
-7
B.
C.
2
D.
1
C©u 31 : 
Tìm m để hàm số đạt cực tiểu tại .
A.
B.
C.
D.
C©u 32 : 
Cho hàm số .Tìm m để hàm số có cực đại , cực tiểu , đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác có diện tích bằng 4 .
A.
B.
C.
D.
C©u 33 : 
Tìm tập xác định D của hàm số sau: 
A.
D = 
B.
D = 
C.
D = 
D.
D = 
C©u 34 : 
Hình vẽ này là đồ thị của hàm số nào sau đây
A.
B.
C.
D.
C©u 35 : 
Tìm m để hàm số ngịch biến trên khoảng (1;3)
A.
B.
m>-1
C.
m>1
D.
m<2
C©u 36 : 
Cho hàm số và các khoảng sau: 
(I). ; (II). ; (III). . 
Hãy tìm các khoảng đồng biến của hàm số trên?
A.
(I) và (II) 
B.
(I) và (III)
C.
(II) và (III)
D.
Chỉ (I).
C©u 37 : 
Cho hàm số , tiệm cận ngang của hàm số trên là:
A.
B.
C.
D.
C©u 38 : 
Cho hàm số . Gọi là giá trị lớn nhất và là giá trị nhỏ nhất của hàm số đã cho. Khi đó: hiệu bằng
A.
B.
C.
D.
C©u 39 : 
Cho hàm số , hàm số đồng biến trên:
A.
B.
C.
D.
C©u 40 : 
Tìm giá trị LN và NN của hàm số 
A.
m=0;M=2
B.
m=0;M=-2
C.
m=-1;M=4
D.
m=1;M=4
C©u 41 : 
Cho hàm số có đồ thị cắt trục tung tại , tiếp tuyến tại A có hệ số góc . Tìm các giá trị a, b: 
A.
B.
C.
D.
C©u 42 : 
Cho hàm sốcó đồ thị (C) và đường thẳng (d): . Trong các điểm: 
(I). (II). (III). 
điểm nào là giao điểm của (C) và (d)?
A.
Chỉ II, III. 
B.
Cả I, II, III.
C.
Chỉ I, II. 
D.
Chỉ III, I. 
C©u 43 : 
Cho hàm số (1), m là tham số thực.
Tìm m để đồ thị hàm số cắt đường thẳng tại 3 điểm phân biệt ; B; C sao cho tam giác có diện tích , với 
A.
B.
C.
D.
C©u 44 : 
Tìm cực trị của hàm số y=sinx-cosx
A.
 và 
B.
C.
D.
 và 
C©u 45 : 
Cho hàm số (1) .Tìm các giá trị của tham số m để đồ thi hàm số (1) có ba điểm cực trị và đường tròn đi qua ba điểm này có bán kính bằng 1.
A.
B.
C.
D.
C©u 46 : 
Giá trị cực đại của hàm số trên khoảng là:
A.
B.
C.
D.
C©u 47 : 
Tìm tập xác định D của hàm số sau: 
A.
D = R\{3}
B.
D = R
C.
D = R\{-1,3}
D.
D = R\{-1}
C©u 48 : 
Với giá trị nào của m thì hàm số nghịch biến trên tập xác định?
A.
B.
C.
D.
 hay 
C©u 49 : 
Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt.
A.
B.
C.
D.
C©u 50 : 
Cho hàm số . Khẳng định nào sau đây đúng
A.
Hàm số đạt cực đại tại gốc tọa độ
B.
Hàm số không có cực trị
C.
Hàm số đạt cực tiểu tại gốc tọa độ
D.
Điểm là điểm cực tiểu
.HẾT.