Một số định lý Hình học

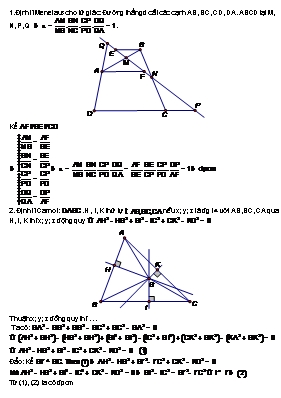
1.Định lí Menelaus cho tứ giác: Đường thẳng d cắt các cạnh AB, BC, CD, DA. ABCD tại M, N, P, Q .
Kẻ 
2. Định lí Carnot: .H , I, K thứ tựnếu x; y; z là đg tvới AB, BC, CA qua H, I, K thì x; y; z động quy 
Thuận: x; y; z đồng quy thì 
 Ta có: 
Đảo: Kẻ 
Từ (1), (2) ta có đpcm
3. Đường tròn Euler: Chân các đg trung tuyến, đg cao, trung đ các đoạn thẳng nối trực tâm với 3 đỉnh là 9 điểm thuộc đg tròn tâm I
4. Đường thẳng Euler: trọng tâm G, trực tâm H, tâm đường tròn nội tiếp O của tam giác thẳng hàng. 
Kẻ đường kính AD của (O) là hình bình hành
là trung điểm HDtrọng tâm G’ của AHD có 
Mà thẳng hàng (đpcm)
5. Định lí con bướm: Cho (O), dây AB, 2 dây CD, EF di động đi qua trung điểm I của AB.
DE, CF cắt AB tại M, N. CMR IM = IN
Kẻ C’D’ đối xứng với CD qua OI
CM tứ giác EC’IM nội tiếp (đpcm)
6.Định lí Steiner: nội tiếp (O). K thuộc cung BC nhỏ. M; N; P đối xứng với K qua BC, AB, CA. CMR M; N; P thẳng hàng.
7. Định lí Newton: Tứ giác ABCD ngoại tiếp (O), tiếp xúc với (O) tại E; F; G; H. Khi đó HG, AC, EF đồng quy
Giả sử . Áp dụng định lí Menelaus cho và MEF
Áp dụng định lí Menelaus đảo chothẳng hàng hay HG, AC, EF đồng quy 
8. Tứ giác ABCD ngoại tiếp (O), tiếp xúc với (O) tại E; F; G; H. Khi đó EG, AC, HF, BD đồng quy
Đặt 
Kẻ 
Đặt . CMTT
Mà AH=AE; CG=CFđồng quy
CMTT ta có đpcm.
9. Định lí Desargues: Nếu có AA’; BB’; CC’ đồng quy; thì P; Q; R thẳng hàng
Để Q; P; R thẳng hàng thì (Menelaus cho)
Menelaus cho 
Thật vậy: Áp dụng định lí Menelaus cho:
Hay P; Q; R thẳng hàng (đpcm).
10. Định lí Pascal: Lục giác ACEBFD nội tiếp có giao điểm các cặp cạnh đối thẳng hàng