Kiểm tra tiết 25 - Năm học 2015- 2016 môn: Hình học lớp 8

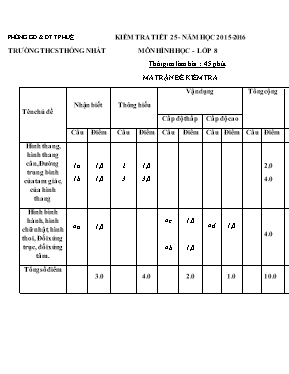
PHÒNG GD & ĐT TP HUẾ KIỂM TRA TIẾT 25 - NĂM HỌC 2015-2016
TRƯỜNG THCS THỐNG NHẤT MÔN HÌNH HỌC - LỚP 8
	 Thời gian làm bài : 45 phút 
 MA TRẬN ĐỀ KIỂM TRA
Tên chủ đề
Nhận biết
Thông hiểu
Vận dụng
 Tổng cộng
Cấp độ thấp
Cấp độ cao
Câu
Điểm
Câu
Điểm
Câu
Điểm
Câu
Điểm
Câu
Điểm
Hình thang, hình thang cân, Đường trung bình của tam giác, của hình thang
1a
1b
1,0
1,0
2
3
1,0
3,0
2,0
4.0
Hình bình hành, hình chữ nhật, hình thoi, Đối xứng trục, đối xứng tâm.
4a
1,0
4c
4b
1.0
1,0
4d
1,0
4.0
Tổng số điểm
3.0
4.0
2.0
1.0
10.0
PHÒNG GD & ĐT TP HUẾ 
 TRƯỜNG THCS THỐNG NHẤT 
 KIỂM TRA TIẾT 25 - NĂM HỌC 2015- 2016
 MÔN: HÌNH HỌC LỚP 8 
 Thời gian làm bài : 45 phút 
ĐỀ KIỂM TRA SỐ ..
Bài 1: (2điểm) Cho hình 1. Tính độ dài x
Bài 2: (1điểm) Cho hình 2. Tính số đo x. Biết F = 750; D = 850; G = 1300.
Bài 3: (3điểm) Cho hình chữ nhật ABCD có AB =2BC, gọi E, F lần lượt là trung điểm của AB và CD.
Chứng minh ADFE là hình vuông?
Bài 4: (4,0 điểm)
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
Chứng minh tứ giác AEBM là hình thoi.
Cho AB =3 cm, AC = 4 cm. Tính chu vi hình thoi AEBM
Tứ giác AEMC là hình gì? Vì sao? 
Gọi I là trung điểm của AM. Chứng minh E, I, C thẳng hàng.
PHÒNG GD & ĐT TP HUẾ KIỂM TRA TIẾT 25 - NĂM HỌC 2015-2016
TRƯỜNG THCS THỐNG NHẤT MÔN: HÌNH HỌC LỚP 8
	ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ KIỂM TRA SỐ: ......
( Đáp án này gồm 03 trang )
BÀI
CÂU
NỘI DUNG
ĐIỂM
1
2,0
a
Trong hình 1:
H là trung điểm của ABI là trung điểm của AC 
Suy ra: HI là đường trung bình của ∆ABC
Nên: HI = 12∙BC
 = 12 ∙ 8
 = 4 (cm )
Vậy: x= 4 cm
0.5
0,5
b
Hình vẽ bài 1 và bài 2
0. 5
0.5
2
1.0đ
Trong tứ giác EDGF ta có :
 E + D + G + F = 3600 ⟹ E = 3600 - ( D + G + F )
 = 3600 - ( 850 + 1300+ 750)
 = 3600 - 2900
 = 700
Vậy : x = 700
0.5
0.5
3
3,0
*ABCD là hình chữ nhật ⟹ AD// BC ; AB// CD
Ta có : E là trung điểm của ABF là trung điểm của CD⟹ EF là đường trung bình của hình thang ABCD; ( AD// BC )
Suy ra: EF//AD (// BC )
Mà AE// DF; ( do AB//DC; E∈ AB; F∈ CD )
Cho nên: AEFD là hình bình hành .
Hình bình hành AEFD có A = 1V, nên AEFD là hình chữ nhật.
Hình chữ nhật AEFD lại có AD= AE, ( Vì cùng bằng 12∙AB )
Do đó AEFD là hình vuông.
0,5
0,5
0.5
0.5
0.5
 0.5
4
4.0đ
a
Ta có: DA = DB, DE = DM (tính chất đối xứng) 
Suy ra: AEBM là hình bình hành.
Ta lại có: MA = 12∙BC (trung tuyến tam giác vuông bằng nửa cạnh huyền).
 MB= 12∙BC, ( M là trung điểm của BC )
Nên: MA= MB
Vậy: AEBM là hình thoi (Hình bình hành có hai cạnh kề bằng nhau).
0,25
0,25
0,25
0,25
b
Áp dụng định lý Pi-ta-go vào tam giác ABC vuông tại A, ta có:
BC2= AB2+ AC2
Mà AB =3 cm, AC = 4 cm
Nên BC2= 32+ 42 = 9+ 16 = 25.
Suy ra: BC= 5 (cm), ( do BC >0 )
*∆ ABC vuông tại A, nên AM= 12∙BC; ( Tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông )
Mà BC= 5cm. Suy ra: AM= 12∙5 = 2,5 (cm)
Vậy: Chu vi hình thoi AEBM là 4∙ 2,5= 10 (cm)
0,25
0,25
0,25
0,25
c
Ta có: AE // BM và AE = BM (vì AEBM là hình thoi).
*Vì AE= BM ; Mà: MC = BM 
Nên AE= MC 
Lại có AE // MC ( Vì AE// BM )
Do đó: AEMC là hình bình hành.
0.5
0.5
d
Trong hình bình hành hai đường chéo cắt nhau tại trung điểm của mỗi đường; mà I là trung điểm của đường chéo AM ,nên I cũng là trung điểm của đường chéo EC .
Vậy: Ba điểm E, I, C thẳng hàng
0.5
0.5
DUYỆT CỦA TỔ TRƯỞNG 
 TỔ TOÁN- LÝ GIÁO VIÊN SOẠN
NGUYỄN VĂN CHƠN HOÀNG TRỌNG LÂM