Kiểm tra chương II môn: Hình học 7 - Trường THCS Trần Phú

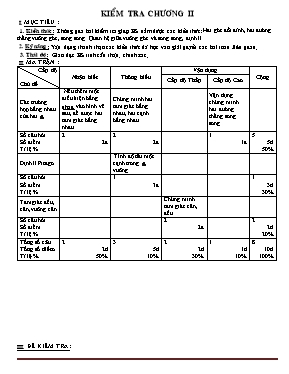
 KIỂM TRA CHƯƠNG II
 I. MỤC TIÊU :
 1. Kiến thức: Thông qua bài kiểm tra giúp HS nắm được các kiến thức:Hai gĩc đối đỉnh, hai đường thẳng vuơng gĩc, song song. Quan hệ giữa vuơng gĩc và song song, định lí.
 2. Kỹ năng: Vận dụng thành thạo các kiến thức đã học vào giải quyết các bài toán liên quan.
 3. Thái độ: Giáo dục HS tính cẩn thận, chính xác.
 II. MA TRẬN :
 Cấp độ
Chủ đề
Nhận biết
Thơng hiểu
Vận dụng
Cộng
Cấp độ Thấp
Cấp độ Cao
Các trường hợp bằng nhau của hai 
 Nêu thêm một điều kiện bằng nhau vào hình vẽ sau, để được hai tam giác bằng nhau
Chứng minh hai tam giác bằng nhau, hai cạnh bằng nhau
Vận dụng chứng minh hai đường thẳng song song.
Số câu hỏi
Số điểm
Tỉ lệ %
2
2đ
2
2đ
1
1đ
5
5đ
50%
Định lí Pitago
 Tính độ dài một cạnh trong vuơng
Số câu hỏi
Số điểm
Tỉ lệ %
1
3đ
1
3đ
30%
Tam giác đều, cân, vuơng cân
Chứng minh tam giác cân, đều
Số câu hỏi
Số điểm
Tỉ lệ %
2
2đ
2
2đ
20%
Tổng số câu
Tổng số điểm
Tỉ lệ %
2
2đ 
50%
3
5đ
10%
2
2đ 
30%
1
1đ 
10%
8
10đ 
100%
III. ĐỀ KIỂM TRA:
Trường THCS Trần Phú	 KIỂM TRA CHƯƠNG II
Họ và tên: 	 Mơn: Hình học – lớp 7
Lớp: 	 Thời gian: 45 phút
Điểm 
Lời phê của giáo viên:
ĐỀ :
M
Câu 1: (2.0 điểm) Nêu thêm một điều kiện bằng nhau vào hình vẽ sau, để được hai tam giác bằng nhau theo các trường hợp bằng nhau đã học:
A
N
P
S
C
B
E
R
T
D
F
Hình 2
Hình 1
Câu 2: (3.0 điểm) Cho ABC nhọn, kẻ AH vuơng gĩc với BC (H BC). 
Cho biết AC = 20 cm, AH = 12cm, BH = 5cm. Tính độ dài cạnh HC, BC, AB.
Câu 3: (5,0 điểm) Cho ABC cân tại A kẻ AHBC (HBC)
Chứng minh:AHB=AHC
Chứng minh: HB = HC.
Kẻ HDAB (DAB) , HEAC (EAC): Chứng minh HDE cân.
Nếu cho = 1200 thì HDE trở thành tam giác gì? Vì sao?
Chứng minh BC // DE.
IV. ĐÁP ÁN VÀ BIỂU ĐIỂM:
ĐÁP ÁN
BIỂU ĐIỂM
Câu 1: Hình 1: BC = DF
 Hình 2: NP = ST
1 điểm
1 điểm
A
Câu 2: 
H
B
C
HC2 = AC2 – AH2 = 202 – 122 = 16 (cm).
BC = BH + HC = 5 + 16 = 21(cm)
AB2 = AH2 + BH2 = 122 + 52 = 13 (cm).
0.5 điểm
1 điểm
0.5 điểm
1 điểm
Câu 3:
I
A
B
D
E
H
C
a) Xét vàcó:
 AB = AC (gt)
 AH là cạnh chung
=> = (c. huyền-c. gĩc vuơng)
b) Vì: = nên HB = HC (hai cạnh tương ứng)
c) Chứng minh :BDH=CEH (cạnh huyền - gĩc nhọn)
 DH = HE 
Vậy HDE cân tại H
d) HED là tam giác đều vì = 
 =
 = 
Tam giác cân cĩ một gĩc bằng 600 là tam giác đều.
e) Gọi 
DIH = EIH (c.g.c)
Mà 
Do đĩ: = 
 AHDE
Mặt khác: AHBC
Do đĩ: DE // BC
0.5 điểm
1 điểm
0.5 điểm
1 điểm
1 điểm
1 điểm
(Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa)