Kiểm tra 45 phút (bài số 4) môn: Đại số 9

 Tiết 17
 KIỂM TRA 45 PHÚT( Bài số 1)
 Môn : Đại số 
I. MA TRẬN ĐỀ
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
1. Khái niệm căn bậc hai 
Hiểu được căn bậc hai của một số không âm, căn bậc hai số học.Tính được căn bậc hai số học, căn bậc hai của một số không âm
Hiểu được điều kiện để xác định. 
Số câu 
Số điểm 
Tỉ lệ
½ (Câu 1a)
0,5 
5%
½ (Câu 1b)
0,5
5%
1câu 
1 điểm
10%
2.Các phép biến đổi đơn giản về căn bâc hai
Nhận biết và thực hiện được phép tính nhân ,chia hai căn bậc hai
Vận dụng được các phép biến đổi để giải phương trình, so sánh các căn bậc hai
Tìm GTLN của biểu thức. Tìm giá trị nguyên của biểu thức
Số câu
Số điểm 
Tỉ lệ
½ (Câu2a,b )
1, 0
10 %
2(Câu 3, câu 4)
2,5
25 %
1(Câu 6 )
1,5
15 %
3,5câu 
5,0điểm
50%
3.Rút gọn biểu thức chá căn bậc hai
Biết rút gọn các biểu thức chứa căn bậc hai, 
Số câu
Số điểm 
Tỉ lệ
1(Câu 5)
3,0
30%
1 câu 
3,0
30%
4. Căn bậc ba
Hiểu và tính được căn bậc ba của một số biểu diễn được thành lập phương một số khác 
Số câu 
Số điểm 
Tỉ lệ
½ (Câu2c, d )
0,5
10%
½
0,5điểm
5%
Tổng số câu 
Tổng số điểm
Tỉ lệ 
1
1,5đ
15%
1
1,5đ
15 %
3
5,5đ 55%
1
1,5đ
15%
15câu 
10 điểm
100%
I. ĐỀ BÀI
ĐỀ A
Câu 1 (1,0đ) a) Tìm căn bậc hai số học rồi suy ra căn bậc hai của các số: 121; 6 
 b) Tìm giá trị của x để : xác định?
Câu 2 (2,0đ) Tính a) (a>0). b) . c) . d) 
Câu 3 (1,0đ) Sắp xếp các số sau theo thứ tự tăng dần: 3 ; 2; -4; 4.
Câu 4 (1,5đ) Giải phương trình:
	a) b)= 4 ; c) 
Câu 5(3,0đ) Rút gọn các biểu thức:
 a) A = 
 b) B = ( Với a ≥ 0 , a ≠ 1)
Câu 6(1,5đ) a) Tìm số x nguyên để biểu thức nhận giá trị nguyên
 b)Tìm giá trị lớn nhất của biểu thức C = 
 III. ĐÁP ÁN VÀ BIỂU CHẤM 
Câu
Nội dung
Điểm
Câu 1 (1,0đ) 
a) Căn bậc hai số học của 121 là:
=> căn bậc hai của 121 là:11 và – 11
b) xác định 10+ 2x ≥ 0
 ó 2x ≥ -10
 ó x ≥ -5
0,25đ
0,5đ
0,25đ
0,25đ
0,25đ
Câu 2 (2,0đ) 
a) = ( vì a> 0)
b) = 
c) = = 3 - 4 - 2(-2) = 3
d) == 2
0,5đ
0,5đ
0,5đ
0,5đ
Câu 3 (1,0đ) 
= ;= ;= ; 4= 
Vì < < < 
Vậy < < 4< 
0,5đ
0,25đ
0,25đ
Câu 4 (1,5đ) 
a) =>x = 25 
b)= 4 => x = 9,; x = 1 
c) óóx = 5 
0,5đ
0,5đ
0.5đ
Câu 5 (3,0đ) 
a) A = = 
 A = 
 A = 
b) B = 
 = 
 = 
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
Câu 6 (1,5đ) 
a) ĐK x ≥ 0 , x ≠ 1
Q = 
Ta có 1Z, với x Z, QZ ó Ư(2)
x {0; 4; 9}
 b) C đạt giá trị lớn nhất khi đạt giá trị nhỏ nhất 
Tacó : = 
 = 
=> đạt giá trị nhỏ nhất là: khi 2x-1 = 0 ó x = 0,5
Vậy Max C = khi x =0,5
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
Lớp 9b bỏ câu 6b, cho câu 6 1,0đ; câu 4 2,0đ 
 Tiết 29 KIỂM TRA 45 PHÚT( Bài số 2)
 Môn : Đại số 9
I. MA TRẬN ĐỀ
Cấp độ
Chủ đề
Nhận biêt
Thông hiểu
Vận dung
Cộng
Cấp độ Thấp
Cấp độ Cao
Hàm số bậc nhất và đồ thị
Nhận biết được hàm số bậc nhất ; hàm số đồng biến, nghịch biến 
Biết vẽ đồ thị của hàm số bậc nhất 
y = ax + b ( a0) . 
.
Biết tìm tọa độ giao điểm của hai đồ thị . Tính diện tích một hình, tính các góc
Số câu hỏi
Số điểm
Tỉ lệ %
2(câu1,2)
3,5
35%
½(câu5a)
1,0
10%
½(Câu 5b)
1,5
15%
3
6,0
60%
 Đường thẳng song song và đường thẳng cắt nhau 
 Xác định các dạng đường thẳng liên quan đến đường thắng cắt nhau, song song.
Số câu hỏi
Số điểm
Tỉ lệ %
1(câu4)
3,0
30%
1
3,0
30%
Hệ số góc của đường thẳng 
Viết được phương trình đường thẳng.
Số câu hỏi
Số điểm
Tỉ lệ %
1(câu 3)
1,0
10%
1
1,0
10%
Tổng số câu
Tổng số điểm
Tỉ lệ %
2
3,5
35%
1/2
1,0
10%
1
3,0
30%
1,5
2,5
25%
5
10,0
100%
II . Đề bài: 
Đề A
Câu(1,5điểm) Điểm nào sau đây thuộc đồ thị hàm số y = 2x - 5 ?
 	A(-2; -1) B(1; -3) C(3; 2) 
Câu 2(2,0điểm): Hàm số nào sau đây là hàm số bậc nhất ? Trong các hàm số là hàm số bậc nhất, hàm số nào đồng biến ? Nghịch biến ? 
a); b) ; c) ; d) y = + 3 
Câu 3 (1,0điểm) Viết phương trình của đường thẳng biết đường thẳng đó đi qua điểm (2; 0) và có hệ số góc bằng 2.
Câu 4 (3,0 điểm) Cho hàm số y = (2 - n)x + n - 1 (d)
a) Với giá trị nào của n thì y là hàm số bậc nhất
b) Với giá trị nào của n thì hàm số y đồng biến? nghịch biến
c) Với giá trị nào của n thì đường thẳng (d) song song với đường thẳng y = 3x + 2
d) Với giá trị nào của n thì đường thẳng (d) cắt đường thẳng y = -x + 4 tại một điểm trên trục tung
Câu 5 (2,5 điểm) Cho hai hàm số y = -2x – 4 (d) và y = x + 4 (d’)
a) Vẽ đồ thị hai hàm số trên cùng mặt phẳng tọa độ?
b) Gọi giao điểm của đường thẳng (d) và (d’)với trục Oy là A và B, giao điểm của hai đường thẳng là C. Xác định tọa độ điểm C và tính diện tíchABC? Tính các góc củaABC?
Đề B
Câu 1(1,5điểm) Điểm nào sau đây thuộc đồ thị hàm số y = 2x - 6 ?
 	A (-2; - 2) B (1; - 4) C (3; 2) 
Câu 2(2,0điểm) Hàm số nào sau đây là hàm số bậc nhất ? Trong các hàm số là hàm số bậc nhất, hàm số nào đồng biến? Nghịch biến? Vì sao?
a) ; b) ; 	c) d) y = +3 
 Câu 3 (1,0điểm) Viết phương trình của đường thẳng biết đường thẳng đó đi qua điểm (1; 0) và có hệ số góc bằng 3
Câu 4: (3,0 điểm) Cho hàm số y = (2 - m)x + m - 1 (d)
a) Với giá trị nào của m thì y là hàm số bậc nhất
b) Với giá trị nào của m thì hàm số y đồng biến? nghịch biến.
c) Với giá trị nào của m thì đường thẳng (d) song song với đường thẳng y = 3x + 2
d) Với giá trị nào của m thì đường thẳng (d) cắt đường thẳng y = -x + 4 tại một điểm trên trục tung
Câu 5 (2,5 điểm) Cho hai hàm số y = x + 4 (d) và y = -2x – 4 (d’)
a) Vẽ đồ thị hai hàm số trên cùng mặt phẳng tọa độ?
b) Gọi giao điểm của đường thẳng (d) và (d’)với trục Oy là M và N, giao điểm của hai đường thẳng là P. Xác định tọa độ điểm P và tính diện tíchMNP? Tính các góc củaMNP?
V. ĐÁP ÁN- BIỂU CHẤM
Đề A
Câu
Đáp án
Điểm
Câu 1 (1,5điểm)
Điểm A không thuộc đồ thị hàm số. Vì 2.(-2) - 5 = -9 -1 
Điểm B thuộc đồ thị hàm số. Vì 2.1 - 5 = - 3 
Điểm C không thuộc đồ thị hàm số. Vì 2.3 - 5 = 1 2
0,5
0,5
0,5
Câu 2
(2,0điểm)
Các hàm số bậc nhất là: c) ; 
 d) y = + 3 
Hàm số c) đồng biến vì 3 > 0
Hàm số d) y = + 3 nghịch biến vì < 0
0,5
0,5
0,5
0,5
Câu 3 (1,0điểm)
Phương trình đường thẳng có dạng:y = ax + b(a0) 
Vì hệ số góc của đường thẳng là 2 => a = 2 
Vì đường thẳng đi qua điểm (2; 0) => x = 2; y = 0
ta có: 0 = 2.2 + b => b = -4 Vậy phương trình đường thẳng: y = 2x – 4 
0,25
0,25
0,25
0,25
Câu 4 (3,0điểm)
a) y là hàm số bậc nhất khi và chỉ khi: 2 – n 0 => n 2 
b) Hàm số y đồng biến khi: 2 – n > 0 => n < 2 
 Hàm số y nghịch biến khi : 2 – n n > 2 
c) Đường thẳng (d) song song với đường thẳng y = 3x + 2 khi và chỉ khi: 
d) Đường thẳng (d) cắt đường thẳng y = -x + 4 tại một điểm trên trục tung khi và chỉ khi: 
0,5
0,5
0,5
0,75
0,75
Câu 5
(2,5điểm)
>
^
a) Xác định đúng các điểm thuộc đồ thị
 Vẽ đúng đồ thị 2 hàm số 
b) Vì C là giao điểm của hai đường thẳng (d ) và ( d’) nên ta có phương trình hoành độ giao điểm: -2x - 4 = x + 4 -3x = 8 x = y = x + 4 = -+ 4 = 
Vậy C( ;)
SABC = AB. CH = .8 .= 
c) Áp dụng tỉ số lượng giác vào tam giác vuông AOF ta có:
tan A = = 26034’
Tam giác vuông BOD ta có: OB = OD = 4 nên là tam giác vuông cân =450
Tam giác ABC có = 1800
Suy ra = 1800 – (26034’ + 450) = 108026’ 
1,0
0,5
0,5
0,5
Đề B
Câu
Đáp án
Điểm
Câu 1 (1,5điểm)
Điểm A không thuộc đồ thị hàm số. Vì 2.(-2) - 6 = -10 -2 
Điểm B thuộc đồ thị hàm số. Vì 2.1 - 6 = - 4 
Điểm A không thuộc đồ thị hàm số. Vì 2.3 - 6 = 0 2
0,5
0,5
0,5
Câu 2
(2,0điểm)
Các hàm số bậc nhất là: c) 
 d) y = +3 
Hàm số c) đồng biến vì 4 > 0
Hàm số d) y = + 3 nghịch biến vì < 0
0,5
0,5
0,5
0,5
Câu 3 (1,0điểm)
Phương trình đường thẳng có dạng:y = ax + b(a0) 
Vì hệ số góc của đường thẳng là 3 => a = 3 
Vì đường thẳng đi qua điểm (1; 0) => x = 1; y = 0
ta có: 0 = 3.2 + b => b = - 6 Vậy phương trình đường thẳng: y = 3x – 6 
0,25
0,25
0,25
0,25
Câu 4 (3,0điểm)
a) y là hàm số bậc nhất khi và chỉ khi: 2 – m 0 => m 2 
b) Hàm số y đồng biến khi: 2 – m > 0 => m < 2 
 Hàm số y nghịch biến khi : 2 – m m > 2 
c) Đường thẳng (d) song song với đường thẳng y = 3x + 2 khi và chỉ khi: 
d) Đường thẳng (d) cắt đường thẳng y = -x + 4 tại một điểm trên trục tung khi và chỉ khi: 
0,5
0,5
0,5
0,75
0,75
Câu 5
(2,5điểm)
>
^
a) Xác định đúng các điểm thuộc đồ thị
 Vẽ đúng đồ thị 2 hàm số 
b) Vì P là giao điểm của hai đường thẳng (d ) và ( d’) nên ta có phương trình hoành độ giao điểm: -2x - 4 = x + 4 -3x = 8 x = y = x + 4 = -+ 4 = 
Vậy P( ;)
SMNP = PH. MN = .8 .= 
c) Áp dụng tỉ số lượng giác vào tam giác vuông AOF ta có:
tan N = = 26034’
Tam giác vuông MOD ta có: OM = OD = 4 nên là tam giác vuông cân =450
Tam giác MNP có = 1800
Suy ra = 1800 – (26034’ + 450) = 108026’ 
1,0
0,5
0,5
0,5
Tiết 46 KIỂM TRA 45 PHÚT( Bài số 3)
 Môn : Đại số 9 . 
I. MA TRẬN ĐỀ
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Í 
Chủ đề 1: Phương trình bậc nhất hai ẩn
Nhận biết phương trình bậc nhất hai ẩn
Biết được khi nào một cặp số (x0;y0) là một nghiệm của pt 
ax + by =c
Số câu
Số điểm 
Tỉ lệ %
1(câu1)
1,0
10%
1(câu 2)
1,0
10%
2
2,0
20%
Chủ đề 2:
Hệ hai phương trình bậc nhất hai ẩn
Dùng vị trí tương đối giữa hai đường thẳng đoán nhận số nghiệm của hệ pt
Số câu
Số điểm 
Tỉ lệ %
1(câu 3)
2,0
2%
1
2.0
20%
Chủ đề 3: Giải hệ phương trình bằng phương pháp cộng đại số, phương pháp thế.
Giải được hệ pt bậc nhất hai ẩn bằng phương pháp cộng đại số và phương pháp thế
Tìm được tham số m để cặp số (x0;y0) thảo mãn đk cho trước
Số câu
Số điểm 
Tỉ lệ %
1(câu4)
2.0
20%
1(câu 5)
2.0
20%
2
4,0
40%
Chủ đề 4:
Giải bài toán bằng cách lập hệ phương trình.
Giải được bài toán, bằng cách lập hệ phương trình
Số câu
Số điểm 
Tỉ lệ %
1(câu 6)
2.0
20%
1
2,0
20%
Tổng só câu
Tổng số điểm
Tỉ lệ %
1
1,0
10%
2
3.0
30%
2
4,0
40%
1
2,0
20%
6
10,0
100%
II. ĐỀ BÀI
Câu1(1,0đ). Phương trình nào sau đây là phương trình bậc nhất 2 ẩn ?
a) 3x2 + 2y = -1 b) 3x = -1 c) 3x – 2y = 0 d) + y = 3
Câu 2(1,0đ). Phương trình bậc nhất 2 ẩn ax + by = c có bao nhiêu nghiệm? Viết nghiệm tổng quát của phương trình?
 Câu 3(2,0đ). Đoán nhận số nghiệm của mỗi phương trình sau:
a) b) c) d) 
 Câu 4(2,0đ) Giải các hệ phương trình sau: 
a) b) 
 Câu 5(2,0đ) Cho hệ phương trình 
a) Với giá trị nào của k thì hệ phương trình có nghiệm là (x; y) = (2 ; -1).
b)Với giá trị nào của k thì hệ phương trình có nghiệm duy nhất ? Hệ phương trình vô nghiệm ?
Câu 6(2,0đ) Giải bài toán sau bằng cách lập hệ phương trình :
Tìm hai số tự nhiên biết rằng tổng của chúng bằng 360 và ba lần số thứ nhất hơn hai lần số thứ hai là 880.
III. ĐÁP ÁN VÀ BIỂU CHẤM
Câu1(1,0đ). Các phương trình sau đây là phương trình bậc nhất 2 ẩn:
b) 3x = -1 c) 3x – 2y = 0
Câu 2(1,0đ). Phương trình bậc nhất 2 ẩn ax + by = c có vô số nghiệm
Nghiệm tổng quát: 
Câu 3(2,0đ). a) vô nghiệm b) vô số nghiệm
c) có nghiệm duy nhất d) có nghiệm duy nhất
Câu 4(2,0đ)
 a) - Khử được ẩn x hoặc y (0,25đ)
 - Tìm được x=1 ; y=1 (0,5đ )
 - Kết luận nghiệm của hệ phương trình là ( x=1 ; y=1 ) (0,25đ)
b) - Đặt ẩn phụ và ĐK của ẩn (0,25đ)
 - Khử được ẩn u hoặc v (0,25đ)
 - Tìm được x= -1 ; y =1/2 (0,25đ )
 - Kết luận nghiệm của hệ phương trình là ( x= -1 ; y =1/2 ) (0,25đ)
Câu 5(2,0đ) 
a) Thay x = 2, y = -1 vào phương trình (1) , ta có : 
2k – (-1) = 5 =>2k = 4 =>k =2 (0,5đ)
Và x = 2 ; y = -1 thoã mãn phương trình(2) (0,5đ)
Vậy với k=2,hệ phương trình có nghiệm là (x;y)=(2; -1) (0,25đ)
b)Hệ phương trình có nghiệm duy nhất (0,5đ)
 Hệ phương trình vô nghiệm , k 5. Vậy k = -1 (0,5đ)
Câu 6(2,0đ) 
Gọi số thứ nhất là x, số thứ hai là y. ĐK x 0, y 0 ( 0,25đ)
Theo bài ra:
Tổng của hai số đó bằng 360 nên ta có phương trình : 
 x + y = 360 (1) (0,5đ)
Ba lần số thứ nhất hơn hai lần số thứ hai là 880, ta có phương trình:
 3x – 2y = 880 (2) (0,5đ)
Vậy ta có hệ phương trình:
Gải hệ phương trình ta được x = 320, y = 40 ( TMĐK). (0,5đ)
Trả lời : Số thứ nhất là 320, số thứ hai là 40. (0,25đ)
(HS giải cách khác đúng vẫn cho điểm tối đa)
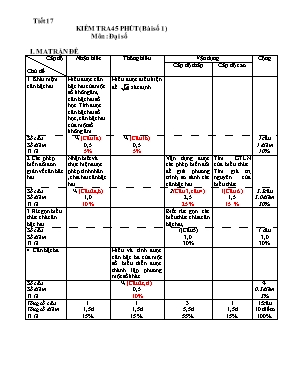
Tiết 66 KIỂM TRA 45 PHÚT( Bài số 4)
 Môn : Đại số 9. 
I. MA TRẬN ĐỀ 	
MA TRẬN ĐỀ KIỂM TRA CHƯƠNG IV - ĐẠI SỐ 9
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TN
TL
TN
TL
1.Hàm số 
y = ax2
Vẽ được đồ thị h/số y = ax2 và tìm được tọa độ giao điểm của (P) và (d)
Số câu
Số điểm
%
1 
2.0
20%
1
2,0
20%
2.Phương trình bậc hai một ẩn
Biết giải phương trình bậc hai
Vận dụng kiến thức về phương trình bậc hai để chứng minh phương trình có nghiệm
Số câu
Số điểm
%
1 
2.0
20%
1
1,0
10%
2
3,0
30%
3.Hệ thức 
Vi-et và áp dụng
Vận dụng được hệ thức Vi-ét và các ứng dụng của nó:Tính giá trị của biểu thức biết nghiệm phương trình
Số câu 
Số điểm
%
1
3,0
30%
1
3,0
30%
4. Giải bài toán bằng cách lập phương trình
Vận dụng các bước giải bài toán bằng cách lập phương trình để giải
Số câu 
Số điểm
%
1
2,0
20%
1
2,0
20%
Tổng số câu
Tổngsố điểm
1 
2.0
20%
3 
7.0
70%
1 
1.0
10%
5
 10
100%
ĐỀ BÀI
Bài 1 (2,0điểm)Cho hai hàm số: y = x2 (P) và y = - 2x + 3 (d).
 a/ Vẽ hai đồ thị (P) và (d) trên cùng một hệ trục toạ độ.
 b/ Tìm toạ độ giao điểm của (P) và (d) bằng phương pháp đại số.
Bài 2: (2 điểm) Giải phương trình: 
	a) 3x2 - 8x + 5 = 0 b) 5x2 - 6x - 11 = 0 
Bài 3.(3,0điểm) Cho phương trình: x2 – 2x + m – 1 = 0(m là tham số)
Giải phương trình với m = 0
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt?
Xác định m để các nghiệm x1, x2 của phương trình thõa mãn: x12 + x22 = 10
Bài 4(2,0điểm) Giải bài toán sau bằng cách lập phương trình .
 Cạnh huyền của tam giác vuông bằng 10 cm . Hai cạnh góc vuông hơn kém nhau 2m .Tính các cạnh góc vuông . 
Bài 5 (1,0điểm) Chứng tỏ rằng phương trình sau 
 (x - a)(x - b) + ( x - b) (x - c) + (x - c) (x - a) = 0 luôn có nghiệm
ĐÁP ÁN VÀ BIỂU ĐIỂM
Bài 1 (2 điểm ) : Mỗi phần 1 điểm .
*) Hàm số y = x2:Bảng một số giá trị tương ứng (x,y):
x
-3
-2
-1
0
1
2
3
y = x2
9
4
1
0
1
4
9
*) Hàm số y = -2x + 3:
- Giao điểm của đồ thị với Oy: A(0; 3). 
Giao điểm của đồ thị với Ox: B(; 0)
- Đường thẳng AB là đồ thị hàm số y = -2x + 3
b) Tìm đúng 2 toạ độ giao điểm 
bằng phương pháp đại số : (1; 1) và (-3; 9) (1 điểm )
Bài 2: (2 điểm). Mỗi câu 1 điểm
a) 3x2 - 8x + 5 = 0 
Ta có 16 – 3.5 = 1 > 0 	( 0,5 điểm)
Phương trình có hai nghiệm phân biệt là 	(0,5 điểm)
b) Ta có 5 –(-6) = (-11) = 0	 (0,5 điểm)
Vậy phương trình có hai nghiệm x1 = -1; x2 = 11 ( 0,5 điểm)
Bài 3: (2 điểm). Mỗi câu 1 điểm
	a) Giải được phương trình 	
	Thế đúng m vào phương trình : 	(0,25đ)
	Xác định đúng a,b, c và tính đúng biệt thức	(0,25đ)
	Tính đúng hai nghiệm	(0,25đ)
	Kết luận đúng 	(0,25đ)
	b)	Xác định phương trình có 2 nghiệm phân biệt thì m > - 4	(1,0đ)
	c) Tìm đúng giá trị m 	 
	Xác định điều kiện của m để phương trình có nghiệm . 	(0,25đ)
	Lập được công thức để tính x1 + x2 	 (0,25đ)
	Lập được các giá trị của x1 + x2 ; x1.x2 theo m	(0,25đ)
	Thế đúng giá trị của x1 + x2 ; x1.x2 vào biểu thức x12 + x12 = 10 (0,25đ)
	Tính đúng và kết luận đúng giá trị của m	(0,25đ)
Bài 4 : (2,0 đ) 
Chọn ẩn đặt điều kiện cho ẩn 	(0,25đ)
Viết được biểu thức tương quan 	(0,5đ)
Lập được phương trình (0,5đ)
Giải phương trình (0,5đ)
 Kết luận	 (0,25đ)
Bài 5 (1,0điểm) 
(x - a)(x - b) + ( x - b) (x - c) + (x - c) (x - a) = 0 
Biến đổi phương trình: (x - a)(x - b) + ( x - b) (x - c) + (x - c) (x - a) = 0
Về dạng 3x2- 2(a+b+c)x + ab + bc + ca= 0_Ta có: 
Vì (a - b)2 0; (b - c)2 0; (c - a)2 0 với mọi giá trị a, b, c
Nên với mọi giá trị a, b, c. Vậy phương trình luôn có nghiệm._
Chú ý : Học sinh làm cách khác nếu đúng vẫn cho điểm tối đa.