Hình học lớp 8 - Tiết 25: Kiểm tra 1 tiết

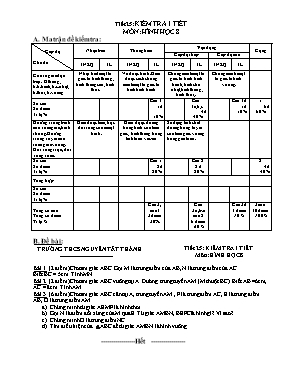
Tiết 25: KIỂM TRA 1 TIẾT
MÔN: HÌNH HỌC 8
A. Ma trận đề kiểm tra:
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Các tứ giác đặc biệt: H thang, h.b.hành, h.c.nhật, h.thoi, h. vuông 
Nhận biết một tứ giác là hình thang, hình thang cân, hình thoi.
Vẽ được hình. Hiểu được cách chứng minh một tứ giác là hình bình hành 
Chứng minh một tứ giác là hình bình hành, hình chữ nhật,hình thang, hình thoi, .
Chứng minh một tứ giác là hình vuông.
Số câu
Số điểm
Tỉ lệ %
Câu 3
1đ
 10%
Câu 3a,b,c
4đ
 40%
Câu 3d
1đ
 10%
1
6đ
60%
Đường trung bình của tam giác, hình thang. Đường trung tuyến của tam giác vuông.
Đối xứng trục, đối xứng tâm.
Hiểu được tâm, trục đối xứng củua một hình.
Hiểu đựợc đường trung bình của tam giác, hình thang trong tính toán và c/m
Sủ dụng tính chất đường trung tuyến của tam giác vuông 
trong giải toán.
Số câu
Số điểm
Tỉ lệ %
Câu 1
2đ 
20%
Câu 2
2 đ 
20%
2
4đ 
 40%
Tổng hợp
Số câu
Số điểm
Tỉ lệ %
Tổng số câu
Tổng số điểm
Tỉ lệ %
Câu 3, câu1
3 điểm 
30%
Câu 3a,b.c câu 2
6 điểm 
60%
Câu 3d
1 điểm 
10%
3 câu
10 điểm 
100%
B. Đề bài:
TRƯỜNG THCS NGUYỄN TẤT THÀNH
Tiết 25: KIỂM TRA 1 TIẾT 
Môn: HÌNH HỌC 8
Bài 1. (2 điểm)Cho tam giác ABC. Gọi M là trung điểm của AB, N là trung điểm của AC. 
Biết BC = 5cm. Tính MN.
Bài 2. (2 điểm)Cho tam giác ABC vuông tại A. Đường trung tuyến AM (M thuộc BC). Biết AB =6cm, AC = 8cm. Tính AM.
Bài 3. (6 điểm)Cho tam giác ABC cân tại A, trung tuyến AM , F là trung điểm AC, E là trung điểm AB, O là trung điểm AM.
Chứng minh tứ giác AEMF là hình thoi.
Gọi N là điểm đối xứng của M qua E. Tứ giác AMBN, BEFClà hình gì? Vì sao?
Chứng minh O là trung điểm NC
Tìm điều kiện của ABC để tứ giác AMBN là hình vuông .
-----------------Hết -----------------
C. Đáp án – Biểu chấm.
TRƯỜNG THCS NGUYỄN TẤT THÀNH
ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT 
Môn: HÌNH HỌC 8
Bài 1: Ta có: EA = EB, FA = FC (gt) nên EF là đường trung bình của tam giác ABC.	(1 điểm)
Suy ra: EF = BC : 2 = 5 : 2 = 2,5 (cm)	(1 điểm)
Bài 2: Áp dụng định lý Py – Ta – Go vào tam giác ABC vuông tại A ta có: 
	BC2 = AB2 + AC2 = 62 + 82 = 100
	Suy ra : BC = 10(cm)	 (1 điểm)	
	Vì AM là đường trung tuyến ứng với cạnh huyền BC nên 
	AM = BC : 2 = 10: 2 = 5(cm) (1 điểm)
Bài 3: Vẽ hình, ghi GT, KL đúng 	(1 điểm)
	Chứng minh:	
Ta có: EA = EB,MB = MC (gt) nên EM là đường trung bình của tam giác ABC.
Suy ra: EM//AC hay EM//AE
	và EM = AE (cùng bằng AC:2)
	Do đó tứ giác AEMF là hình bình hành. (1)	(1 điểm)
	Ta lại có tam giác ABC cân tại A nên đường trung tuyến AM đồng thời là đường phân giác.(2)
	Từ (1) và (2) suy ra AEMF là hình thoi.	(0,5 điểm)
Tứ giác AMBN có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Mà tam giác ABC cân tại A nên đường trung tuyến AM đồng thời là đường cao 
nên 
Hình bình hành AMBN có nên là hình chữ nhật.	(1 điểm)
Ta có: EA = EB,MB = MC (gt) nên EM là đường trung bình của tam giác ABC.
Suy ra: EF//BC 
	Do đó tứ giác BEFC là hình thang. 	(0,5 điểm)
Tứ giác MNAC có NA//MC và NA = MC ( cùng bằng MB ) nên là hình bình hành.
Suy ra hai đường chéo AM và NC cắt nhau tại trung điểm mỗi đường. 
Mà O là trung điểm của AM nên O là trung điểm của NC.	(1 điểm)
Hình chữ nhật AMBN là hình vuông
AM = MB
(vì )
vuông cân tại A.	(1 điểm)	
	Phú xuân, ngày 15/11/2016
	Giáo viên ra đề và đáp án
	Đào Thị Lý