Giáo án Hình học 8 tiết 19: Đường thẳng song song với một đường thẳng cho trước (tiếp)

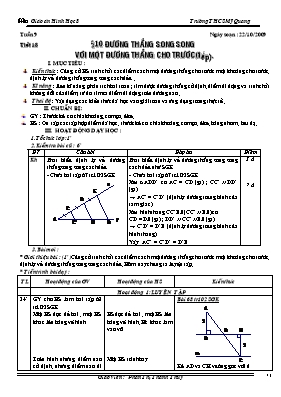
Tuần 9 Ngày soạn :22/10/2009
Tiết 18 §10 ĐƯỜNG THẲNG SONG SONG 
VỚI MỘT ĐƯỜNG THẲNG CHO TRƯỚC(tiếp).
 I. MỤC TIÊU : 
Kiến thức : Củng cố HS tính chất các điểm cách một đường thẳng cho trước một khoảng cho trước, định lý về đường thẳng song song cách đều . 
Kĩ năng : Rèn kĩ năng phân tích bài toán ; tìm được đường thẳng cố định, điểm di động và tính chất không đổi của điểm, từ đó tìm ra điểm di động trên đường nào .
Thái độ : Vận dụng các kiến thức đã học vào giải toán và ứng dụng trong thực tế .
 II. CHUẨN BỊ :
GV : Thước kẻ có chia khoảng, compa, êke.
HS : Oân tập các tập hợp điểm đã học, thước kẻ có chia khoảng, compa, êke, bảng nhóm, bút dạ.
 III. HOẠT ĐỘNG DẠY HỌC :
 1.Tổ chức lớp :1’ 
 2.Kiểm tra bài cũ : 6’
ĐT
Câu hỏi
Đáp án
Điểm
Kh
Phát biểu định lý về đường thẳng song song cách đều 
- Chữa bài tập 67 tr 102 SGK
Phát biểu định lý về đường thẳng song song cách đều như SGK
- Chữa bài tập 67 tr 102 SGK
Xét DADD’ có AC = CD (gt) ; CC’ // DD’ (gt)
Þ AC’ = C’D’ (định lý đường trung bình của tam giác) 
Xét hình thang CC’BE (CC’ // BE) có 
CD = DE (gt) ; DD’ // CC’ // BE (gt)
Þ C’D’ = D’B (định lý đường trung bình của hình thang)
Vậy AC’ = C’D’ = D’B
3 đ
7 đ
 3.Bài mới :
* Giới thiệu bài : (1’)Củng cố tính chất các điểm cách một đường thẳng cho trước một khoảng cho trước, định lý về đường thẳng song song cách đều. Hôm nay chúng ta luyện tập.
* Tiến trình bài dạy :
TL 
Hoạt động của GV 
Hoạt động của HS 
Kiến thức
Hoạt động 1:LUYỆN TẬP
34’
GV cho HS làm bài tập 68 tr102 SGK
Một HS đọc đề bài , một HS khác lên bảng vẽ hình 
Trên hình những điểm nào cố định, những điểm nào di động ?
Khi điểm B di động trên đường thẳng d thì điểm C di động trên đường thẳng nào ? vì sao ?
GV Cho HS làm bài 70 SGK
Gọi một HS đọc đề bài , yêu cầu HS hoạt động nhóm
Sau khi các nhóm hoạt động khoảng 5 phút, đại diện hai nhóm lên bảng trình bày hai cách chứng minh.
GV nhận xét bài làm của một số nhóm
Yêu cầu HS nhắc lại hai tập hợp điểm.
Đường thẳng song song với một đường thẳng cho trước
Đường trung trực của một đoạn thẳng
GV đưa đề bài 71 tr 103 SGK lên bảng phụ, gọi một HS lên bảng vẽ hình 
Yêu cầu HS viết GT, KL của bài toán 
a)Chứng minh A, O, M thẳng hàng
 GV ta đã vận dụng kiến thức nào để chứng minh ba điểm thẳng hàng .
b)Khi điểm M đi chuyển trên BC thì O di chuyển trên đường nào ?
(tương tự như bài tập 70 SGK)
c) Điểm M ở vị trí nào trên cạnh BC thì AM có độ dài nhỏ nhất ? vì sao ?
HS đọc đề bài , một HS lên bảng vẽ hình, Hs khác làm vào vở
Một HS trình bày 
Một HS đọc to đề bài 
HS hoạt động theo nhóm
Đại diện hai nhóm lên bảng trình bày, HS các nhóm khác nhận xét 
HS trả lời
Một HS lên bảng vẽ hình và viết GT, KL, HS cả lớp làm vào vở
Một HS lên bảng trình bày câu a
Ta đã vận dụng tính chất đường chéo của hình chữ nhật để chứng minh ba điểm thẳng hàng
Một HS khác trình bày miệng câu b
HS trả lời 
Nếu M º H thì AM = AH, khi đó AM có độ dài nhỏ nhất (đường vuông góc ngắn hơn mọi đường xiên)
Bài 68 tr102 SGK
Kẻ AD và CH vuông góc với d
Xét hai tam giác vuông ADB và CHB có 
AB = BC (gt)
 (đối đỉnh)
Nên DADB = DCHB (cạnh huyền- góc nhọn)
Þ CH = AD = 2 cm
Điểm C cách đường thẳng d cố định một khoảng không đổi 2 cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm
Bài 70 tr103 SGK
Cách 1 :
Kẻ CH ^ Ox.
DAOB có AC = CB (gt) 
CH // AO (cùng vuông góc với Ox)
Þ CH là đường trung bình của DAOB
Þ CH = (cm)
Nếu B º O Þ C º E (Elà trung điểm của AO)
Vậy khi B di chuyển trên tia Ox thì C di chuyển trên tia Em song song với Ox và cách Ox một khoảng bằng 1 cm
Cách 2 :
Nối CO 
Tam giác vuông AOB có 
OC là đường trung tuyến (AC = CB)
Þ OC = AC = (tính chất tam giác vuông)
Có OA cố định Þ C di chuyển trên tia Em thuộc đường trung trực của đoạn thẳng OA.
Bài 71 tr103 SGK
GT
DABC có 
M Ỵ BC; MD ^ AB
ME ^ AC; OD = OE
KL
a) A, O, M thẳng hàng
b) Khi M di chuyển trên BC thì O di chuyển trên đường nào 
 c) M ở vị trí nào thì AM nhỏ nhất
 Chứng minh :
 a) Xét tứ giác AEMD có 
 (gt) 
Þ AEMD là hình chữ nhật
Có O là trung điểm của đường chéo DE nên O củng là trung điểm của đường chéo AM
Þ A, O, M thẳng hàng 
b) Kẻ AH ^ BC và OK ^ BC
Þ OK // AH
mà AO = OM (gt) 
Þ OK là đường trung bình của tam giác AHM
Þ OK = (không đổi)
Nếu điểm M º B thì O º P (P là trung điểm của AB)
Nếu M º C thì O º Q (Q là trung điểm của AC)
Vậy khi M di chuyển trên BC thì O di chuyển trên đường trung bình PQ của DABC
c) Nếu M º H thì AM = AH, khi đó AM có độ dài nhỏ nhất (đường vuông góc ngắn hơn mọi đường xiên)
1’
Hoạt động 2CỦNG CỐ
GV yêu cầu HS nhắc lại tập hợp các điểm cách đường thẳng cố định một khoảng không đổi.
HS phát biểu.
	4.Hướng dẫn về nhà :2’
Xem lại các bài tập đã chữa
Bài tập về nhà 127, 128, 129, 130 tr 73 SBT
Oân tập định nghĩa, tính chất, dấu hiệu nhận biết của hình bình hành, hình chữ nhật, tam giác cân.
	IV. RÚT KINH NGHIỆM, BỔ SUNG: