Giáo án chương 1: Dao động điều hòa

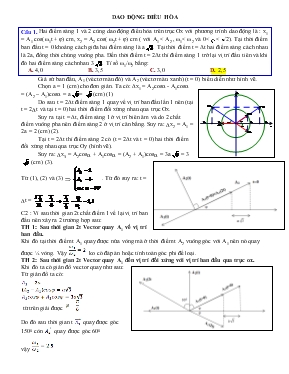
DAO ĐỘNG ĐIỀU HỊA
Hai điểm sáng 1 và 2 cùng dao động điều hịa trên trục Ox với phương trình dao động là : x1 = A1 cos(ω1t + φ) cm, x2 = A2 cos( ω2t + φ) cm ( với A1 < A2 , ω1< ω2 và 0< < /2). Tại thời điểm ban đầu t = 0 khoảng cách giữa hai điểm sáng là a. Tại thời điểm t = Δt hai điểm sáng cách nhau là 2a, đồng thời chúng vuơng pha. Đến thời điểm t = 2Δt thì điểm sáng 1 trở lại vị trí đầu tiên và khi đĩ hai điểm sáng cách nhau 3. Tỉ số ω1/ω2 bằng: 
	A. 4,0 	B. 3,5 	 C. 3,0 	 D. 2,5 
Giả sử ban đầu, A1 (véctơ màu đỏ) và A2 (véctơ màu xanh) (t = 0) biểu diễn như hình vẽ.
Chọn a = 1 (cm) cho đơn giản. Ta cĩ: Dx1 = A2cosa - A1cosa = (A2 – A1)cosa = a= (cm) (1)
Do sau t = 2Dt điểm sáng 1 quay về vị trí ban đầu lần 1 nên (tại t = 2Dt và tại t = 0) hai thời điểm đối xứng nhau qua trục Ox.
Suy ra tại t = Dt, điểm sáng 1 ở vị trí biên âm và do 2 chất điểm vuơng pha nên điểm sáng 2 ở vị trí cân bằng. Suy ra: Dx2 = A1 = 2a = 2 (cm) (2).
Tại t = 2Dt thì điểm sáng 2 cĩ (t = 2Dt và t = 0) hai thời điểm đối xứng nhau qua trục Oy (hình vẽ).
Suy ra: Dx3 = A2cosa + A1cosa = (A2 + A1)cosa = 3a = 3 (cm) (3).
Từ (1), (2) và (3) Þ . Từ đĩ suy ra: t = Dt = 
C2 : Vì sau thời gian 2t chất điểm 1 về lại vị trí ban đầu nên xảy ra 2 trường hợp sau: 
TH 1: Sau thời gian 2t Vector quay A1 về vị trí ban đầu.
Khi đĩ tại thời điểm t A1 quay được nửa vịng mà ở thời điểm t A2 vuơng gĩc với A1 nên nĩ quay được ¼ vịng. Vậy ko cĩ đáp án hoặc tính tốn gĩc phi để loại.
TH 2: Sau thời gian 2t Vector quay A1 đến vị trí đối xứng với vị trí ban đầu qua trục ox.
Khi đĩ ta cĩ giản đồ vector quay như sau:
Từ giản đồ ta cĩ: 
 từ trên giải được 
Do đĩ sau thời gian t quay được gĩc 1500 cịn quay được gĩc 600 
vậy 
Câu 2: Dao động tổng hợp của hai dao động điều hịa cùng phương, cùng tần số cĩ biên độ bằng trung bình cộng của hai biên độ thành phần; cĩ gĩc lệch pha so với dao động thành phần thứ nhất là 900. Gĩc lệch pha của hai dao động thành phần đĩ là
A. 1200.	B. 126,90.	C. 143,10.	D. 1050.
Ta cĩ: A1 + A2 = 2A, dựa vào giản đồ: 
Từ đĩ Þ A2 = 5A/4 Þ cosa = A/A2 Þ a = 36,90 Þ độ lệch pha của 2 dao động là: 900 + 36,90 = 126,90
Câu 3: Hai vật dao động điều hịa cĩ cùng tần số gĩc là. Tổng biên độ dao động của hai vật là 10 cm. Trong quá trình dao động vật một cĩ biên độ A1 qua vị trí x1 ( cm ) với vận tốc v1 ( cm/s ), vật hai cĩ biên độ A2 qua vị trí x2 ( cm ) với vận tốc v2 ( cm/s ). Biết. Giá trị của cĩ thể là:
A. 0,1 rad/s B. 0,4 rad/s C. 0,2 rad/s D. 0,3 rad/s
Ta cĩ: (BĐT Bunhiacopxki)
Biến đổi: (BĐT cosi)
Từ đĩ suy ra: (rad/s) chọn B.
Câu 4: Một vật thực hiện một dao động điêu hịa x = Acos(2πt + φ) là kết quả tổng hợp của hai dao động điều hịa cùng phương cĩ phương trình dao động x1 = 12cos(2πt + φ1) cm và x2 = A2cos(2πt + φ2) cm. Khi x1 = - 6 cm thì x = - 5 cm; khi x2 = 0 thì.Giá trị của A cĩ thể là :
A. 15,32cm 	B. 14,27cm 	C. 13,11cm 	D. 11,83cm 
Ta cĩ: x = x1 + x2.
Tại thời điểm t1: x2 = x – x1 = 1 (cm) và x1 = A1/2.
Trên vịng trịn cĩ 2 vị trí cĩ li độ x1 = -6, chọn 1 vị trí cố định.
Tại thời điểm t2 : x1 = x – x2 = (cm) = 
Trên vịng vịng cĩ 2 vị trí cĩ li độ x1 = (chọn 1 vị trí để giải, nếu cĩ đáp án thì chọn, khơng cĩ giải trường hợp cịn lại là đúng).
Cung màu đỏ biểu diễn véctơ quay của A1 từ t1 đến t2 là 1500.
Từ đĩ suy ra véctơ quay của A2 cũng quay 1500 từ t1 đến t2 như hình vẽ.
Dễ dàng suy ra A2 = 2 (cm), tại thời điểm t1, A1 và A2 lệch nhau 600 (độ lệch pha khơng đổi theo thời gian).
Suy ra : (cm).
Câu 5: Khi đưa một vật lên một hành tinh, vật ấy chỉ chịu một lực hấp dẫn bằng 0,25 lực hấp dẫn mà nĩ chịu trên trái đất. Giả sử một đồng hồ quả lắc chạy rất chính xác trên bề mặt Trái đất được đưa lên hành tinh đĩ. Khi kim phút của đồng hồ này quay được một vịng thì thời gian trong thực tế là: 
A. 0.5h 	B. 4h 	C. 2h 	D. 0.25h
Giải: Do P’ = 0,25P nên g’ = 0,25g
 Trên bề mặt rái đất: T = 2π; Trên hành tinh: T’ = 2π = 2π = 2T
 Do đĩ khi T’ = 1h thì T = 0,5h. Đáp án A
Câu 6: Một ơ tơ nặng 1000 kg chở 4 người, mỗi người nặng 60 kg đi qua con đường đất gồ ghề, với những nếp gấp (chỗ gồ ghề) cách đều nhau 4,5m. Ơ tơ nảy lên với biên độ cực đại khi tốc độ của nĩ là 16,2 km/h. Bây giờ ơ tơ dừng lại và 4 người ra khỏi xe. Lấy g = 10m/s2, p2 = 10. Thân xe sẽ nâng cao trên hệ treo của nĩ một đoạn là
A. 4,8cm	B. 48cm	C. 24cm	D. 2,4cm
Giải: vận tốc v = 16,2 km/h = 4,5 m/ s
Ơ tơ nảy lên với biên độ cực đại khi chu kỳ dao động của lị xo T = = = 1 s
 T = 2π --à Độ cứng của lị xo k = = = 49,6.103 N/m
Khi 4 người xuống xe thân xe sẽ nâng cao trên hệ treo một đoạn
 Dl = = = 0,048m = 4,8 cm. Đáp án A
Câu 7: Hai vật dao động điều hịa cĩ cùng tần số gĩc là. Tổng biên độ dao động của hai vật là 10 cm. Trong quá trình dao động vật một cĩ biên độ A1 qua vị trí x1 ( cm ) với vận tốc v1 ( cm/s ), vật hai cĩ biên độ A2 qua vị trí x2 ( cm ) với vận tốc v2 ( cm/s ). Biết. Giá trị của cĩ thể là:
A. 0,1 rad/s B. 0,4 rad/s C. 0,2 rad/s D. 0,3 rad/s
Ta cĩ: (BĐT Bunhiacopxki)
Biến đổi: (BĐT cosi)
Từ đĩ suy ra: (rad/s) chọn B.
Câu 8: Một vật dao động điều hịa với phương trình x =Acos(t + ) . Lấy . Vị trí mà vận tốc tức thời bằng vận tốc trung bình của vật trong một chu kì cĩ tọa độ là :
A. 	B. 	C. 	D. 
Giải : x =Acos(t + ) => v = - ω A sin (ωt + φ)
Trong 1 chu kỳ thì vtb = 4A/T= 2Aω /π 
Thay v = vtb vào phương trình độc lập với thời gian => x2 = A2 – v2/ ω2 = 3A2/5 => x = => D và A
Câu 9: Hai vật dao động điều hịa theo hai trục tọa độ song song cùng chiều. Phương trình dao động của hai vật tương ứng là x1 = Acos(3πt + φ1) và x2 = Acos(4πt + φ2). Tại thời điểm ban đầu, hai vật đều cĩ li độ bằng A/2 nhưng vật thứ nhất đi theo chiều dương trục tọa độ, vật thứ hai đi theo chiều âm trục tọa độ. Khoảng thời gian ngắn nhất để trạng thái của hai vật lặp lại như ban đầu là:
	A. 4s.	B. 1 s.	C. 2s.	D. 3s.
Giải: 
Câu 10: Hai chất điểm M và N cĩ cùng khối lượng, dao động điều hịa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua gốc tọa độ và vuơng gĩc với Ox. Biên độ của M là 6 cm, của N là 8 cm. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 10 cm. Mốc thế năng tại vị trí cân bằng. Ở thời điểm mà M cĩ động năng bằng thế năng, tỉ số động năng của M và động năng của N là
	A. .	B. .	C. .	D. .
Giải:
	Khoảng cách 2 vật: 
	Suy ra x1. x2 vuơng pha
Khi tại M cĩ động năng bằng thế năng : 
Do N,M dao động vuơng pha: 
	Do đĩ: 
 Câu 11: Cho 3 dao động điều hịa cùng phương cùng tần số cĩ phương trình lần lượt là x1 = A1cos(ωt + φ1); x2 = A2cos(ωt + φ2) và x3 = A3cos(ωt + φ3). Biết A1 = 1,5A3; φ3 – φ1 = π. Gọi x12 = x1 + x2 là dao động tổng hợp của dao động thứ nhất và dao động thứ hai; x23 = x2 + x3 là dao động tổng hợp của dao động thứ hai và dao động thứ ba. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ hai dao động tổng hợp trên là như hình vẽ. Giá trị của A2 là: 
A. A2 ≈ 3,17 cm 	B. A2 ≈ 6,15 cm	C. A2 ≈ 4,87 cm	D. A2 ≈ 8,25 cm
A1
A3
A2
A12
A23
300
600
Theo đồ thị cĩ x23=4cos(pt+p/2) cm=x2+x3 vì x12 sau cực đại âm sau x23 T/6 nên nĩ chậm pha hơn p/3
=>x12=8cos(pt+p/6) cm=x2+x1
Cách 1: A1 = 1,5A3; φ3 – φ1 = π ĩ x1=-1,5x3
1,5x23=6cos(pt+p/2)=1,5x2+1,5x3 	 
x12=8cos(pt+p/6) cm=
6cos(pt+p/2)+ 8cos(pt+p/6)= 1,5x2+1,5x3 +x2+x1=1,5x2+x2=2,5x2=2Ư37cos(pt+55,3p/180)cm ĩA2=4,866
Cách 2: x12- x23=x1-x3=8cos(pt+p/6) - 4cos(pt+p/2) = 43cos(pt)
vì A1 = 1,5A3; φ3 – φ1 = π nên φ1=0 (đồng pha với φ1-3)
A3=cm
Dj= 0,6 X2
X1
X
-X2
y
 X2
Câu 12: Hai chất điểm dao động điều hịa cùng tần số, trên hai đường thẳng song song với nhau và song song với trục Ox cĩ phương trình lần lượt là và . Gỉa sử và . Biết biên độ dao động của gấp 2 lần biên độ dao động của . Độ lệch pha cực đại giữa và gần với giá trị nào nhất sau đây:
	A. 36,870 	B. 53,140 	C. 143,140 	D. 126,870 
Giải: Đặt Dj = j2 - j1 . Gọi biên độ của y là A; khi đĩ biên độ của x là 2A.
Vẽ giãn đồ véc tơ biễu diễn x1, x2, x và y 
Ta cĩ: 4A2 = A12 + A22 + 2A1A2cosDj (1)
 A2 = A12 + A22 - 2A1A2cosDj (2)
 Lấy (1) + (2): 5A2 =2( A12 + A22) (*)
(1) - (2): 3A2 = 4A1A2cosDj (**)
 Từ (*) và (**) cosDj = = 0,3( X + ) với X = >0
Độ lệch pha giữa x1 và x2 Dj cĩ giá trị cực đại khi cosDj cĩ giá trị cực tiểu
 cosDj = 0,3( X + ) cĩ giá trị cực tiểu khi X = 1 tức khi A1 = A2 
-----à cosDjmax = 0,6 -----à Djmax = 53,130 Chọn đáp án B
Câu 13: Cho hai chất điểm dao động điều hồ cùng phương, cùng tần số, cĩ phương trình dao động tương ứng là : Biết rằng Khi chất điểm thứ nhất cĩ li độ , vận tốc bằng 9 m/s thì vận tốc của chất điểm thứ hai cĩ độ lớn bằng:
A. 8 cm/s.	B. 12 cm/s.	C. 6 cm/s.	D. 9 cm/s.
Giải:
 lấy đạo hàm 
Câu 14: Hai vật dao động điều hịa dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox sao cho khơng va chạm vào nhau trong quá trình dao động. Vị trí cân bằng của hai vật đều ở trên một đường thẳng qua gốc tọa độ và vuơng gĩc với Ox. Biết phương trình dao động của hai vật lần lượt là và . Tính từ t = 0, hai vật cách nhau 2 cm lần thứ 2013 tại thời điểm:
	A. 	B. 	C. 	D. 	
 Giải:
Bấm máy tính để xác định ptdd khoảng cách: 
+ 
Trong một chu kỳ thì vật cĩ k/c d=2cm 4 lần(hiển thị trên hình). Kết quả: 
Câu 15: Một chất điểm dao động điều hồ khơng ma sát dọc theo trục Ox. Biết rằng trong quá trình khảo sát chất điểm chưa đổi chiều chuyển động. Khi vừa rời khỏi vị trí cân bằng một đoạn s thì động năng của chất điểm là 13,95 mJ. Đi tiếp một đoạn s nữa thì động năng của chất điểm chỉ cịn 12,60 mJ. Nếu chất điểm đi thêm một đoạn s nữa thì động năng của nĩ khi đĩ là:
 A. 11,25 mJ. B. 8,95 mJ. C. 10,35 mJ. D. 6,68 mJ.
Giải: Theo định luật bảo tồn cơ năng: 
Từ đĩ suy ra: 
Thay (1) vào (2) được ⟹ Chọn C.
Câu 16: Dụng cụ đo khối lượng trong một con tàu vũ trụ cĩ cấu tạo gồm một chiếc ghế cĩ khối lượng m được gắn vào đầu của một chiếc lị xo cĩ độ cứng k = 480 N/m. Để đo khối lượng của nhà du hành thì nhà du hành phải ngồi vào ghế rồi cho chiếc ghế dao động. Người ta đo được chu kì dao động của ghế khi khơng cĩ người là T0 = 1 s cịn khi cĩ nhà du hành là T = 2,5 s. Khối lượng nhà du hành là
A. 80 kg.
B. 63 kg.
C. 75 kg.
D. 70 kg.
Giải:
- Nhận xét: Chiếc ghế cĩ cấu tạo giống như một con lắc lị xo treo thẳng đứng, ghế ở phía trên, lị xo ở phía dưới. Gọi khối lượng của ghế là m (kg), của người là m0 (kg).
- Khi chưa cĩ người ngồi vào ghế: (1).
- Khi cĩ người ngồi vào ghế: (2).
- Từ (1) và (2), ta cĩ: 
Câu 17: Hai chất điểm dao động điều hồ trên hai trục tọa độ Ox và Oy vuơng gĩc với nhau (O là vị trí cần bằng của cả hai chất điểm). Biết phương trình dao động của hai chất điểm là: x = 2cos(5πt +π/2)cm và y =4cos(5πt – π/6)cm. Khi chất điểm thứ nhất cĩ li độ x =cm và đang đi theo chiều âm thì khoảng cách giữa hai chất điểm là
A. cm.	B. cm.	C. cm.	D. cm.
Giải : Chọn D
t = 0: 	x = 0, vx< 0 chất điểm qua VTCB theo chiều âm
	y =, vy >0, chất điểm y đi từ ra biên. 
* Khi chất điểm x đi từ VTCB đến vị trí hết thời gian T/6
* Trong thời gian T/6 đó, chất điểm y đi từ ra biên dương rời về lại đúng 
* Vị trí của 2 vật như hình vẽ
Khoảng cách giữa 2 vật là cm 
Câu 18: Hai điểm sáng M và N dao động điều hịa trên trục Ox (gốc O là vị trí cân bằng của chúng) với phương trình lần lượt là x1=53cos(4 t+ π/2)cm; x2 =10cos(4π t + 2π /3) cm. Khoảng cách cực đại giữa hai điểm sáng là
A. 5 13 cm. B. 8,5cm. C. 5cm. D. 15,7cm.
Giải : Chọn C
Câu 19: Hai vật dao động điều hịa dọc theo hai trục tọa độ song song cùng chiều. Phương trình dao động của hai vật tương ứng là x1 = Acos(3πt + j1) và x2 = Acos(4πt + j2) . Tại thời điểm ban đầu, hai vật đều cĩ li độ bằng A/2 nhưng vật thứ nhất đi theo chiều dương trục tọa độ, vật thứ hai đi theo chiều âm trục tọa độ. Khoảng thời gian ngắn nhất để trạng thái của hai vật lặp lại như ban đầu là:
A. 4s 	B. 3s 	 C. 2s 	D. 1s
Giải: Chu kì dao động của 2 vật: T1 = = = (s); T2 = = = (s)
Khoảng thời gian để trạng thái của hai vật lặp lại như ban đầu là:
 t = n1T1 = n2T2 với n1; n2 nguyên dương => n1 = n2 => n1 = 3n; n2 = 4n
 Do đĩ t = 3nT1 = 4nT2 = 2n (s). n = 0 ứng với t = 0
Khoảng thời gian ngắn nhất để trạng thái của hai vật lặp lại như ban đầu là t = 2 (s) (n = 1)
 Đáp án C
II
IV
M7
I
O
x
A
A/2
30
M1
M4
-A
A
30
M6
M2
A
M5
M3
Câu 20 : Một chất điểm đang dao động điều hồ trên một đường thẳng mà trên đĩ cĩ 7 điểm M1,M2,M3,M4,M5,M6,M7 xung quanh vị trí cân bằng O trùng M4 . . Cho biết trong quá trình dao động cứ 0,05s thì chất điểm lại đi qua các điểm M1,M2,M3, O(M4), M5,M6,M7 và tốc độ của nĩ lúc đi qua các điểm M2 là 20π cm/s. Biên độ A bằng?
A. 4cm	 B.6cm 	 C.12cm	D. 4cm
Cách : Dùng vịng trịn lượng giác : 
Theo đề suy ra gĩc quay ứng 0,05s là 300 hay p/6 
Mà chu kỳ T ứng 2p Hay T= 0,05. 2p/ p/6 =0,6s 
=> 
 Biên độ:
Câu 21: Mợt vật có khới lượng khơng đởi thực hiện đờng thời hai dao đợng điều hòa và , phương trình dao đợng tởng hợp của vật là . Để vật dao đợng với biên đợ bằng mợt nửa giá trị cực đại của biên đợ thì A2 bằng bao nhiêu?
 A. 10 cm 	 B. 20cm 	 C. 20 / cm D. 10/ cm
 Giải 1:
Mà ta có 
∆
p/3
p/6
p/6
φ
α
O
 =>Amax = . Để A = Amax/2 = 10 thi .
Giải 2: Ta cĩ: 
Phương trình trên luơn cĩ nghiệm nên: 
Khi A=10(cm) từ (*) suy ra: 
Giải 3:
* Định lý hàm số sin trong tam giác 
à à Amax = 20cm khi α = 900
* Khi A=Amax/2 =10 cm à Dùng định lý hàm số cos trong à . 
Câu 22: Một vật dao động điều hịa với phương trình x = A.cos(ωt). Tỉ số giữa tốc độ trung bình và vận tốc trung bình khi vật đi được sau thời gian 3T/4 đầu tiên kể từ lúc bắt đầu dao động là:
A. 1/3 	B. 3 	C. 2 	D. 1/2
Giải:
Vận tốc trung bình: , là độ dời. Vận tốc trung bình trong một chu kỳ luơn bằng khơng
Tốc độ trung bình luơn khác 0: trong đĩ S là quãng đường vật đi được từ t1 đến t2.
Tốc độ trung bình: (1); chu kỳ đầu vật đi từ x1 = + A (t1 = 0) đến x2 = 0 (t2 = ) (VTCB theo chiều dương) 
Vận tốc trung bình: (2). Từ (1) và (2) suy ra kết quả bằng 3.
Câu 23: Một vật dao động điều hịa với phương trình li độ: x = 4cos(8πt –2π/3) cm. Thời gian vật đi được quãng đường S = (2 + 2) cm kể từ lúc bắt đầu dao động là:
A. 1/12 	B. 5/66 	C. 1/45 	D. 5/96
Giải:
 Vật xuất phát từ M đến N thì đi được quãng đường S = 2 + 2. Thời gian: 
Câu 24: Một chất điểm dao động đh trên trục Ox.Tốc độ trung bình của chất điểm tương ứng với khoảng thời gian thế năng khơng vượt quá 3 lần động năng trong 1 nửa chu kì là 300√3 (cm/s)Tốc độ cực đại của dao động là:
A.400 cm/s B.200 cm/s C.2p m/s D.4p m/s
Giải:
 Thế năng khơng vượt quá 3 lần động năng: 
Gĩc quay AOB=,thời gian quay: 
Quãng đường trong một nửa chu kì ứng chất điểm quay từ A đến B là:
Tốc độ trung bình:
Suy ra vmax=2π (m/s)	
Câu 25: Một chất điểm dao động điều hịa với biên độ A và chu kì là T = 2s. Biết khoảng thời gian ngắn nhất để vật đi từ x1 = 1,8cm theo chiều dương đến x2 = theo chiều âm là 1/6 s. Biên độ của dao động là:
A. A= cm.     	B. A = cm.           C. A = cm.        D.A =  cm
Giải:
gọi pha dao động khi vật cĩ ly độ x2 là  ta cĩ
	(sd giải PT bằng máy tính)
Câu 26: Một vật dao động điều hịa trên trục Ox với biên độ là A = 4cm, khi vật đi qua vị trí cân bằng thì tốc độ của vật là 40cm/s. Tại thời điểm t1 vật cĩ vận tốc v1 = 10 cm/s và gia tốc cĩ giá trị âm. Trước đĩ π/60 s vận tốc của vật cĩ giá trị:
A.  (cm/s). 	B.  (cm/s).
C.  (cm/s).	D. (cm/s).
Giải: 
pha ban đầu của vận tốc (trên trục O v) là  
trước đĩ  tức là lúc đĩ pha của vận tốc là 
vận tốc lúc này  là 
Câu 27: Một vật dao động điều hịa theo phương trình . Trong giây đầu tiên kể từ lúc vật bắt đầu dao động vật đi qua vị trí cĩ ly độ 2cm theo chiều dương mấy lần?
	A. 2.	B. 3.	C. 4.	D. 5
Giải:
	Ta cĩ: 
 	Xét Khi x = 2cm X = 1 cm. 
Khi theo chiều âm
Trong giây đầu tiên vật thực hiện được 2,5 chu kỳ . Trong mỗi chu kỳ vật qua li độ X = 1cm theo chiều dương 1 lần.
Do đĩ trong giây đầu tiên kể từ lúc vật bắt đầu dao động vật đi qua vị trí cĩ ly độ X = 1cm hay x = 2cm theo chiều dương 2 lần
Câu 28: Cho một vật dao động điều hịa với chu kì T. Tìm khoảng thời gian ngắn nhất từ lúc cơng suất lực hồi phục cực đại đến lúc động năng vật gấp ba lần thế năng.
A.T/24	B. T/36	C. T/6	D. T/12
Giải
Giả sử x=Acos
Cơng suất lực hồi phục là: P=F.v=kA.cos.A
khi ( lấy một giá trị dương để tính)
Động năng bằng 3 lân thế năng 
Thời gian ngắn nhất gĩc quét như hình: 
Thời gian : 
Câu 29: Một vật cĩ khối lượng m=100g chuyển động với phương trình (cm;s).Trong đĩ là những hằng số. Biết rằng cứ sau một khoảng thời gian ngắn nhất thì vật lại cách vị trí cân bằng cm. Xác định tốc độ vật và hợp lực tác dụng lên vật tại vị trí x1= - 4cm.
A. 0 cm/s và 1,8N	B. 120cm/s và 0 N	
C. 80 cm/s và 0,8N	D. 32cm/s và 0,9N
Giải:
C1: + Vì khoảng thời gian ngắn nhất để vật cĩ cùng khoảng cách tới VTCB Þ Gĩc pha nhỏ nhất ứng với hai thời điểm đĩ là 3600/4 = 900 hay Dt = T/4 Þ Vị trí cĩ li độ |x’| = 
Þ A = 8cm. và T = Þw = 15(rad/s)
+ Khi x = - 4cm Þ li độ x’ = - 8cm	= -AÞ v = 0
Þ Hợp lực Fhl = - mw2x’= -0,1.152.(-0,08) = 1,8N.
y
4
0
T/4
A
- A
-4
C2:
* => y = x – 4 = Acoswt
* cứ sau một khoảng thời gian ngắn nhất thì vật lại cách vị trí cân bằng cm :
	+ T/4 = => T = p/7,5 (s) => w = 15
	+ A /= => A = 8 cm
* tại vị trí x1= -4cm. => y = - 4 – 4 = - 8 cm = - A
	+ tốc độ vật : v = 0
	+ hợp lực tác dụng lên vat : F = -ky = -22,5.(- 0,08) = 1,8N (k = mw2 = 0,1.152 = 22,5)
	ĐÁP ÁN A
Câu 30: Một vật dao động điều hịa theo phương trình . Tìm thời gian trong chu kì đầu để tọa độ của vật khơng vượt quá -3,5cm.
A. 1/12 s	B.1/8 s	C. 1/4s	D. 1/6 s
Giải:
+ x là tọa độ, li độ x’ = 5cos(4pt - )cm.
+ x £ - 3,5cm Þ x’ £ - 2,5cm = - A/2. 
+ Dt = 2T/3 Þ gĩc quét 2400 như hình bên
Þ Gĩc quét của bán kính thỏa mãn điều kiện bài là: 900ÞDt = T/4 = 1/8(s) Đáp án B.
Câu 31: Một vật dao động điều hịa với phương trình Tại thời điểm pha của dao động bằng lần độ biến thiên pha trong một chu kỳ, tốc độ của vật bằng
A. 	B. 	C. 	D. 
Giải:
+ Độ biến thiên pha dao động trong 1 chu kì là Dj = 2pÞ (wt + j) = 
+ v = -12psin(wt + j) = - 6p (cm/s) Þ Tốc độ |v| = 6p (cm/s)
 Câu 32: Một vật dao động điều hồ với phương trình x = 8cos(2pt-) cm. Thời điểm thứ 2010 vật qua vị trí cĩ vận tốc v = - 8p cm/s là:
	A. 1005,5 s	B. 1004,5 s	C. 1005 s	D. 1004 s	
Giải:	+ v = x’ = 16pcos(2pt + )cm/s.	
	+ t0 = 0 Þ v0 = và đang giảm.
	+ v = - 8p(cm/s) = 	
	Þ t2010 = t2 + = =
Câu 33: Hai chất điểm chuyển động trên quỹ đạo song song sát nhau, cùng gốc tọa độ với các phương trình x1 = 3cos(wt)(cm) và x2 = 4sin(wt)(cm). Khi hai vật ở xa nhau nhất thì chất điểm 1 cĩ li độ bao nhiêu?
	A.± 1,8cm	 	B. 0	C. ± 2,12cm.	D. ± 1,4cm.
Giải:
·Cách 1: Phương pháp giản đồ.
+ Khoảng cách hai chất điểm là hình chiếu của hai đầu mút A1A2 xuống Ox. Và khoảng cách này cực đại khi A1A2 song song với Ox như hình vẽ.
+ Theo hệ thức lượng trong tam giác ta cĩ: Þ= 1,8cm.
·Cách 2: Phương pháp đại số.
+ Khoảng cách hai chất điểm d = |x1 - x2| = 5|cos(wt + )|cm.
Þ Khoảng cách này cực đại dmax = 5cm Þ (wt + ) = ± 1	Þwt = - + kp
+ Li độ của chất điểm 1 là: x1 = 3cos(wt) = 3. (±0,6) = ±1,8cm.
Câu 34: Hai chất điểm M, N dao động điều hịa dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua gốc tọa độ và vuơng gĩc với Ox. Phương trình dao động của chúng lần lượt là x1 = 10cos2πt (cm) và x2 = 10cos(2πt +) (cm) . Hai chất điểm gặp nhau khi chúng đi qua nhau trên đường thẳng vuơng gĩc với trục Ox. Thời điểm lần thứ 2013 hai chất điểm gặp nhau là:
A.16 phút 46,42s.	B. 16 phút 47,42s	
C. 16 phút 46,92s	D. 16 phút 45,92s
Giải:
+ Khoảng cách hai chất điểm d = |x1 - x2| = 20|cos(2pt - )|
+ Khi hai chất điểm đi ngang qua nhau thì d = 0 Þ t = 
Vậy lần thứ 2013 (k = 2013 - 1) hai chất điểm gặp nhau ở thời điểm: t = 16phút 46,4166s = 16 phút 46,42s Đáp án A
Cách 2: Giải: ta cĩ x2 = 10cos(2πt +) cm = - 10sin(2πt ) 
x1 = x2 	=> 10cos(2πt = - 10sin(2πt ) 	=> tan(2πt ) = -
=> 2πt = - + kπ =>