Giải 4 bài toán về Hình vuông

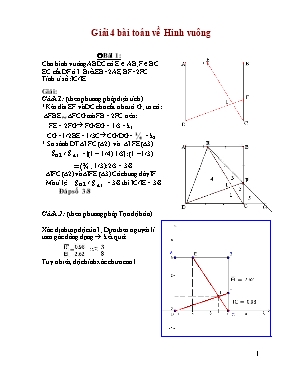
Giải 4 bài toỏn về Hinh vuụng
àBàI 1:
Cho hỡnh vuụng ABDC cú E ẻ AB; Fẻ BC. EC cắt DF ở I. Biết EB=2AE, BF=2FC. 
Tớnh tỉ số: IC/IE
Giải:
Cỏch 1: (theo phương phỏp diện tớch)
*Kộo dài EF và DC cho cắt nhau ở G ; ta cú:
 ∆FBE ~ ∆FCG mà FB = 2FC nờn:
 FE = 2FG à FG/EG = 1/3 = k1
 CG =1/2BE = 1/3C àCG/DG = ẳ = k2
* So sỏnh DT ∆I FC (∆2) và ∆I FE (∆3)
 S∆2 / S ∆3 =[(1 – 1/4).1/3] : (1 – 1/3)
 = (ắ . 1/3): 2/3 = 3/8
 ∆IFC (∆2) và ∆IFE (∆3) Cú chung đỏy IF
 Mà tỉ lệ S∆2 / S ∆3 = 3/8 thỡ IC/IE = 3/8
 Đỏp số 3/8
Cỏch 2 : (theo phương phỏp Tọa độ húa ) 
Xỏc định toạ độ của I ; Dựa theo nguyờn lớ tam gỏc đồng dạng à kết quả:
Tuy nhiờn, độ chớnh xỏc chưa cao ! 
Cỏch 3: (theo PP đồ thị hàm số)
Đưa cỏc yếu tố bà toỏn vào mặt phẳng toạ độ ; Xỏc định 2 hàm số bậc nhất
 ; 
Giải PT 2 hàm số trờn ta cú:
 x = 27/11; y = 9/11
 Theo nguyờn lớ tam gỏc đồng dạng tớnh ra IC/EC = (9/11): (33/11) = 3/11
 ố Vậy IC/ I E = 3/8
àBài 2: 
Trong hỡnh bờn: cỏc hỡnh ABCD, MNPQ và HICK là hỡnh vuụng. 
Tớnh tỉ số diện tớch của hỡnh trũn nằm trong hỡnh vuụng MNPQ và hỡnh trũn nằm trong hỡnh vuụng HICK.
 Giải
Cỏch 1:
Gọi độ dài cạnh AB là a, ta cú AM = a/6; 
Gọi O là giao điểm MP và QN; gọi R là bỏn kớnh hỡnh trũn năm trong hỡnh vuụng MNPQ;
S∆QOM = a/6 x a/6 : 2= ax a /72 = 1/4 S MNPQ; R X R = 1/4 SMNPQ nờn
 S ∆ QOM = R X R = ax a /72;
à Diện tớch hỡnh trũn nằm trong MNPQ = a x a /72 x 3,14.
Mặt khỏc ta cú: IC = a/4; bỏn kớnh hỡnh trũn nằm trong hỡnh vuụng HICK = a/8; diện tớch hỡnh trũn nằm trong hỡnh vuụng HICK= a/8 x a/8 x 3,14
 = a x a /64 x 3,14. 
ố Vậy tỉ số diện tớch hỡnh trũn nằm trong hỡnh vuụng MNPQ và diện tớch hỡnh trũn nằm trong hỡnh vuụng HICK = a x a /72 x 3,14 : a x a /64 x 3,14 
 = 64/72 = 8/9.
Cỏch 2: (Đưa 2 ụ vuụng cú hỡnh trũn cần xột sỏt nhau để dễ quan sỏt)
 - Hỡnh trũn nội tiếp hinh vuụng MNPQ cú đường kớnh là d1
 d1 = cạnh hỡnh vuụng MNPQ = 1/3 PQ (đường chộo hỡnh vuụng cạnh a)
 PQ = à d1 = 
- Hỡnh trũn nội tiếp hinh vuụng HICK cú đường kớnh là d2.d2 = IC = ẵ a
Tỉ lệ diện tớch 2 hỡnh trũn (k) bằng bỡnh phương tỉ lệ 2 đường kinh tương ứng. 
 ố k = (d1/d2)2 = [ ẵ a / ] 2 = 8/9
àBài 3
Đường trũn (O ; R) nội tiếp hỡnh vuụng ABCD và ngoại tiếp hỡnh vuụng MNPQ. Cho AB=2R. 
a/ Tớnh diện tớch phần tụ màu theo R. 
b/ So sỏnh tỷ lệ diện tớch phần tụ màu với phần cũn lại của cả hỡnh vuụng
Giải
Cỏch 1:
Diện tich hỡnh vuụng ABCD là: So = 2R x 2R = 4 R2
Diện tich hỡnh vuụng MNPQ là: S1 = (R.ệ2)2 = 2 R2 
Diện tich hỡnh trũn tõm O là : S2 = π R2
a/ Diện tớch phần tụ màu = diện tớch hỡnh trũn - diện tớch hỡnh vuụng MNPQ.
 S3 = S2 – S1 = π R2 – 2 R2 = R2(π – 2)
b/ Tỷ số phần tụ màu/ phần cũn lại là: [R2(π – 2)]/[(So – S2) + S1] 
= [R2(π – 2)]/[4 R2 – π R2 + 2 R2] = (π – 2) / (6 – π) = # 0,4
Cỏch 2: ( Xột ẳ hỡnh suy ra toàn bộ)
S1 (tam giỏc OMN) = 1/2R2. ( vỡ OM = ON = R)
S2 (Hỡnh quạt OMN) = ẳ πR2 ( Hỡnh quạt = ẳ hinh trũn)
S3 (hỡnh bỏn cung) = S2 – S1 = R2(1/4π – 1/2) = ẳ R2(π – 2)
a/ S tổng 4 Hỡnh bỏn cung = R2 (π – 2) à Đỏp số R2 (π – 2)
b/S4 (hỡnh thang MNAB = SOAB – S1 = 2R2 – R2 = R2
Diện tớch phần trống trong 1 hỡnh thang MNAB: 
 R2 - ẳ R2(π – 2) = ẳ R2 (4 – π )
Tổng diện tớch phần trống: 2R2 + R2(4 – π) = R2( 6 – π)
Tỷ số phần tụ màu/ phần cũn lại là: (π – 2) / (6 – π) = # 0,4
àBài 4
Cho tứ giỏc ABCD cú éADC + éBCD = 900 và AD = BC. Gọi I, N, J, M lần lượt là trung điểm của AB, AC, CD, BD.
Chứng minh tứ giỏc INJM là hỡnh vuụng.
Giải: 
Kộo dài CB và DA cho cắt nhau ở S ta cú tam giỏc vuụng SDC (vuụng ở S vỡ D + C = 900). Theo đề ta cú 
IM là đường trung bỡnh của ABD
NJ là đường trung bỡnh của ACD
AB D và AC D chung đỏy A D à IM =NJ = ẵ AD và IM //NJ
Tương tự ta cú IN =MJ = ẵ BC Mà theo gt BC = A D à MI = NJ = IN = MJ 
Vỡ A D BC nờn cỏc cặp cạnh của ỊN JN; NJ MJ; JM IM; IM IN
IN JM là hỡnh vuụng
PHH sưu tầm đề & biờn soạn bài giải 12 - 2015