Đề thi tuyển sinh Lớp 10 THPT môn Toán - Năm học 2016-2017 - Phòng GD & ĐT Châu Thành (Có đáp án)

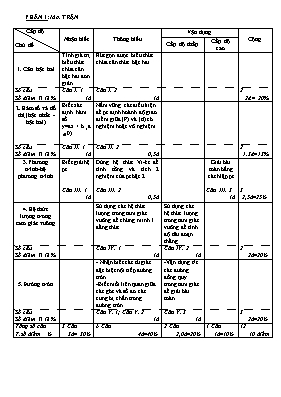
PHẦN I: MA TRẬN 
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Căn bậc hai
Tính giá trị biểu thức chứa căn bậc hai đơn giản
Rút gọn được biểu thức chứa căn thức bậc hai
Số câu 
Số điểm Tỉ lệ %
Câu I. 1
1đ
Câu I. 2
1đ 
2
2đ = 20%
2.Hàm số và đồ thị (bậc nhất - bậc hai)
Biết xác định hàm số 
y=ax + b (a0).
Nắm vững các điều kiện để pt định hoành độ giao điểm giữa (P) và (d) có nghiệm hoặc vô nghiệm
. 
Số câu 
Số điểm Tỉ lệ %
Câu II. 1
1đ
Câu II. 2
0,5đ
2
1,5đ=15%
3.Phương trình-hệ phương trình
Biết giải hệ pt
Dùng hệ thức Vi-ét để tính tổng và tích 2 nghiệm của pt bậc 2 
Giải bài toán bằng cách lập pt
Câu III. 1
1đ
Câu III. 2
0,5đ
Câu III. 3
1đ
3
2,5đ=25%
4.Hệ thức lượng trong tam giác vuông
Sử dụng các hệ thức lượng trong tam giác vuông để chứng minh 1 đẳng thức
Sử dụng các hệ thức lượng trong tam giác vuông để tính độ dài đoạn thẳng
Số câu 
Số điểm Tỉ lệ %
Câu IV. 1
1đ
Câu IV. 2
1đ
2
2đ=20%
5.Đường tròn
- Nhận biết các tứ giác đặc biệt nội tiếp đường tròn.
-Biết mối liên quan giữa các góc và số đo các cung bị chắn trong đường tròn.
-Vận dụng t/c các đường đồng quy trong tam giác để giải bài toán
Số câu 
Số điểm Tỉ lệ %
Câu V. 1; Câu V. 2
1đ
Câu V. 3
1đ
3
2đ=20%
Tổng số câu 
T.số điểm %
3 Câu
3đ= 30%
6 Câu 
4đ=40%
2 Câu
2,0đ=20%
1 Câu 
1đ=10%
12
10 điểm
PHẦN II: ĐỀ THI
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO CHÂU THÀNH
TRƯỜNG THCS PHÚ LONG
 THAM KHẢO 
ĐỀ THI TUYỄN SINH LỚP 10
NĂM HỌC 2016 – 2017
MÔN: TOÁN
Thời gian làm bài: 120 phút
(Không kể thời gian phát đề)
ĐỀ : 
Câu I: (2,0 điểm)
 1. Tính giá trị của biểu thức: (1điểm)
2. Rút gọn biểu thức: , với x0 và x1.(1điểm)
Câu II: (1,5 điểm)
Cho hàm sốcó đồ thị là (P) và hàm số y = k.x + 3 có đồ thị là (d) 
 1. Tìm k biết rằng (d) đi qua điểm M(1;5) (1điểm)
	2. Khi k = 2, chứng tỏ (P) và (d) cắt nhau tại 2 điểm phân biệt (0,5điểm) 
Câu III: (2,5 điểm)
	1. Giải hệ phương trình: (1điểm)
 2. Cho phương trình bậc hai ẩn x, tham số m : x2 – x + (m + 1) = 0 (0.5điểm)
Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn biểu thức: x1 + x2 + x1.x2 = 1
 3. Giải bài toán sau bằng cách lập phương trình: (1điểm)
Quãng đường AB dài 260 km. Hai ôtô khởi hành cùng một lúc đi từ A đến B. Ôtô thứ nhất chạy nhanh hơn ôtô thứ hai 10 km/h, nên đến B trước ôtô thứ hai là 32 phút. Tìm vận tốc của mỗi ôtô.
Câu IV: (2,0 điểm)
Cho ABC cân tại A, kẻ, biết AB = 25cm, BC = 30cm.
1. Từ H kẻ và kẻ . 
Chứng minh rằng: IA.IB = AH.DH (1điểm)
2. Tính AI. (1điểm)
Câu V: (2,0 điểm)
ChoABC (AB >AC; > 900) I; K theo thứ tự là trung điểm của AB, AC. Các đường tròn đường kính AB và AC cắt nhau tại điểm thứ hai D; tia BA cắt đường tròn (K) tại điểm thứ hai E, tia CA cắt đường tròn (I) tại điểm thứ hai F.
1. Chứng minh rằng 3 điểm B;C;D thẳng hàng (0.5 điểm) 
2. Chứng minh rằng tứ giác BFEC nội tiếp (0.5 điểm)
3. Chứng minh 3 đường thẳng AD,BF,CE đồng quy?HẾT. (1điểm)
PHẦN III: HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO CHÂU THÀNH
TRƯỜNG THCS PHÚ LONG
 THAM KHẢO 
HƯỚNG DẪN CHẤM ĐỀ THI TUYỄN SINH LỚP 10
NĂM HỌC 2016 – 2017 
MÔN: TOÁN
Thời gian làm bài: 120 phút
(Không kể thời gian phát đề)
Câu
Nội dung yêu cầu
Điểm
Câu I
(2,0 đ)
1. Tính giá trị của biểu thức:
 Vậy 
0,5
 0,5
2. Rút gọn biểu thức: , với x0 và x1
 Vậy 
0,5
0,25
0,25
Câu II
(2,0 đ)
1. Tìm k biết rằng (d): y = ax + 3 đi qua điểm M(1;5) 
Thay x = 1 ; y = 5 vào (d) ta được : 5 = k .1+ 3 k = 5 – 3 = 2Vậy k = 2
0,5
0,5
2. Khi k = 2, ta có (d): y = 2x +3
Nếu (P) và (d) cắt nhau tại 2 điểm phân biệt thì phương trình định hoành độ giao điểm giữa (P) và (d): có 2 nghiệm phân biệt tức là . 
Thật vậy: đpcm! 
0,25
0,25
Câu III
(2,5 đ)
1. Giải hệ phươngtrình:
 Vậy hệ phương trình có nghiệm duy nhất (x; y) = (5; 2)
2. pt : x2 – x + m + 1 = 0 (1) (có a = 1; b = – 1 ; c = m + 1 )
Để pt(1) có 2 nghiệm x1và x2 thì hay 1 – 4 m – 4 0 m 
Với m thì pt(1) có 2 nghiệm x1và x2 
Theo Vi- ét ta có 
thay vào biểu thức x1 + x2 + x1.x2 = 1 
ta được: 1 + m + 1 = 1 m = – 1 < (thỏa mãn điều kiều kiện)
Vậy khi m = – 1 thì pt(1) có 2 nghiệm x1và x2 thỏa mãn biểu thức
 x1 + x2 + x1.x2 = 1
3. Gọi vận tốc của ôtô thứ nhất là x (km/h); điều kiện : x > 10
Vận tốc của ôtô thứ hai là x – 10 (km/h)
Thời gian ôtô thứ nhất đi hết quãng đường AB là : (h)
Thời gian ôtô thứ hai đi hết quãng đường AB là : (h)
Ta có 32 phút = (h)
Theo đề bài ta có phương trình : 
Giải phương trình ta được x1 = 75> 10 (thỏa mãn điều kiện)
 x2 = - 65 (không thỏa mãn điều kiện)
Vận tốc của ôtô thứ hai là : 75 – 10 = 65 
Trả lời : Vận tốc của mỗi ôtô thứ nhất là 75 (km/h) và vận tốc ôtô thứ hai là 65 (km/h).
0,25
0,25
0,25
0,25
0,25
0,25
 0,25
0,25
0,25
 0,25
Câu IV
(2,0đ)
1. Chứng minh: IA.IB = AH.DH 
 - vuông tại H, đường cao HI 
 Áp dụng hệ thức lượng ta có 
 - Tương tự: vuông tại I có đường cao ID có 
 Từ (1) và (2) IA.IB = AH.DH Đpcm! 
0,25
0,25
0,5
2. ABC cân tại A có đường cao AH HB = HC = 15 cm
-Tính HA : Áp dụng Py ta go ta có cm
-Tính AI:vuông tại H, đường cao HI 
Áp dụng hệ thức lượng ta có 
0,25
0,25
0,25
0,25
Câu V
(2,0đ)
1. Chứng minh rằng 3 điểm B;C;D thẳng hàng 
Có = 900 (Góc nội tiếp chắn nữa đường tròn)
 (góc bẹt
 3 điểm B,D,C thẳng hàng đpcm!
0,25
0,25
2. Chứng minh rằng tứ giác BFEC nội tiếp 
hay = = 900 (cùng nhìn cạnh BC)
 Tứ giác BFEC nôi tiếp đpcm
3. Chứng minh 3 đường thẳng AD,BF,CE đồng quy
Gọi M là giao điểm của BF và CE 
Ta có CFBF CFBM CF là đường cao của MBC
 BECE BECM BE là đường cao của MBC
Mà BE và CF cắt nhau tại A nên A là trực tâm của MBC
Do 3 điểm B;C;D thẳng hàng (cmt) AD BC nên AD củng là đường
cao của MBC 3 đường cao AD,BF,CE của MBC đồng quy tại M 
 đpcm!
0,25
0,25
0,25
0,25
0,25
0,25