Đề thi thử THPT Quốc gia môn Toán - Trường THPT C Hải Hậu (Có đáp án)

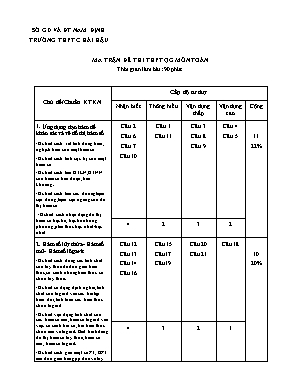
SỞ GD VÀ ĐT NAM ĐỊNH
TRƯỜNG THPT C HẢI HẬU
MA TRẬN ĐỀ THI THPT QG MƠN TỐN
Thời gian làm bài: 90 phút.	
Chủ đề/Chuẩn KTKN
Cấp độ tư duy
Nhận biết
Thơng hiểu
Vận dụng thấp
Vận dụng cao
Cộng
1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
-Hs biết cách xét tính đồng biến, nghịch biến của một hàm số
-Hs biết cách tính cực trị của một hàm số
-Hs biết cách tìm GTLN,GTNN của hàm số trên đoạn, trên khoảng.
-Hs biết cách tìm các đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
 -Hs biết cách nhận dạng đồ thị hàm số bậc ba, bậc bốn trùng phương,phân thức bậc nhất /bậc nhất
Câu 2
Câu 6
Câu 7
Câu 10
Câu 1
Câu 11
Câu 3
Câu 8
Câu 9
Câu 4
Câu 5
11
22%
4
2
3
2
2. Hàm số lũy thừa- Hàm số mũ- Hàm số lơgarit
-Hs biết cách dùng các tính chất của lũy thừa để đơn giản biểu thức,so sánh những biểu thức cĩ chứa lũy thừa.
-Hs biết sử dụng định nghĩa, tính chất của logarit vào các bài tập biến đổi, tính tốn các biểu thức chứa logarit
-Hs biết vận dụng tính chất của các hàm số mũ, hàm số logarit vào việc so sánh hai số, hai biểu thức chứa mũ và logarit. Biết hình dáng đồ thị hàm số lũy thừa, hàm số mũ, hàm số logarit.
-Hs biết cách giải một số PT, BPT mũ đơn giản bằng pp đưa về lũy thừa cùng cơ số, logarit hĩa, dùng ẩn phụ , sử dụng tính chất hàm số
 -Hs biết cách giải một số PT, BPT mũ đơn giản bằng pp đưa về logarit cùng cơ số, mũ hĩa ,dùng ẩn phụ.
Câu 12
Câu 13
Câu 14
Câu 16
Câu 15
Câu17
Câu19
Câu 20
Câu 21
Câu 18
10
20%
4
3
2
1
3. Nguyên hàm – Tích phân và ứng dụng
-Hs biết cách tìm nguyên hàm dựa vào bảng nguyên hàm và cách tính nguyên hàm từng phần.Sử dụng pp đổi biến.
-Hs biết cáchtính tích phân của một số hàm số đơn giản bằng định nghĩa,pp tính tích phân từng phần, pp đởi biến số.
-Hs biết cách tính diện tích một số hình phẳng, thể tích một số khối trịn xoay nhờ tính tích phân.
Câu 22
Câu 24
Câu 25
Câu 23
Câu 27
Câu 28
Câu 26
7
14%
3
3
1
0
4. Số phức
-Hs biết cách cộng trừ, nhân chia số phức.
-Hs biết cách tìm nghiệm phức của PT bậc hai với hệ số thực.
Câu 33
Câu 34
Câu 29
Câu 30
Câu 31
Câu 32
6
12%
2
1
3
0
5. Khối đa diện
-Hs biết cách phân chia khối đa diện, các khối đa diện đều, tính thể tích các khối: chĩp, lăng trụ
Câu 35
Câu 36
Câu 40
Câu 37
Câu 39
Câu 38
Câu 41
7
14%
0
3
2
2
6. Mặt nĩn – Mặt trụ - Mặt cầu
-Hs biết cách xác định, tính thể tích , diện tích, mặt nĩn, mặt trụ, mặt cầu
Câu 42
Câu 43
2
4%
0
0
2
0
7. Phương pháp tọa độ trong khơng gian
-Hs biết cách tính tọa độ của tổng, hiệu hai véc tơ,,tích một véc tơ với một số, tính được tích cĩ hướng, tích vơ hướng của hai véc tơ, tính được khoảng cách giữa hai điểm, viết được phương trình mặt cầu.
-Hs biết cách xác định véc tơ pháp tuyến của một mặt phẳng, biết cách viết phương trình của mặt phẳng, tính được khoảng cách từ một điểm đến một mp.
-Hs biết cách viết phương trình tham số của đường thẳng, biết xét vị trí tương đối của hai đường thẳng khi biết phương trình của hai mặt phẳng đĩ.
Câu 47
Câu 48
Câu 44
Câu 45
Câu 46
Câu 49
Câu 50
7
14%
2
3
2
0
Cộng
15
(30%)
15
(30%)
15
(30%)
5
(10%)
50
BẢNG MƠ TẢ CHI TIẾT NỘI DUNG CÂU HỎI ĐỀ THI THPT QG
CHỦ ĐỀ
CÂU
MƠ TẢ
1.Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
1
Thơng hiểu: Chỉ ra GTLN, NN trên một đoạn
2
Nhận biết: Nhận dạng đồ thị hàm số bậc ba
3
Vận dụng: Tìm GTLN của hàm số gắn với bài tốn hình học
4
Vận dụng cao: Tìm điều kiện của tham số m để hàm số đồng biến trên một khoảng
5
Vận dụng cao: Tìm GTNN của biểu thức hai biến
6
Nhận biết: Tiệm cận đứng, tiệm cận ngang của đồ thị
7
Nhận biết: Viết phương trình tiếp tuyến tại điểm
8
Vận dụng: Tìm điều kiện của tham số m để hàm số trùng phương đạt cực trị tại x = 0
9
Vận dụng: Tìm số giao điểm của hai đồ thị bằng bảng biến thiên
10
Nhận biết: Tìm điểm cực trị của hàm số
11
Thơng hiểu:Chỉ ra số giao điểm của hai đồ thị dựa vào đồ thị đã cho
2. Hàm số lũy thừa- Hàm số mũ- Hàm số lơgarit
12
Nhận biết: Tính giá trị của biểu thức lũy thừa
13
Nhận biết: Phương trình mũ cơ bản
14
Nhận biết: Tính đạo hàm của hàm số mũ
15
Thơng hiểu: Giải phương trình mũ bằng PP đặt ẩn phụ
16
Nhận biết: Phương trình lơgarit cơ bản
17
Thơng hiểu: Giải phương trình logarit bằng cách sử dụng tính chất của logarit
18
Vận dụng cao: Bài tốn lãi suất ngân hàng
19
Thơng hiểu: Phương trình mũ kết hợp lơgarit
20
Vận dụng: Giải phương trình mũ cĩ chứa căn thức
21
Vận dụng: Tìm điều kiện của tham số m để phương trình mũ cĩ nghiệm
3. Nguyên hàm – Tích phân và ứng dụng
22
Nhận biết: Tính chất của nguyên hàm
23
Thơng hiểu: Tính tích phân bằng PP chen cận
24
Nhận biết: Phương pháp đổi biến để tính tích phân
25
Nhận biết: Diện tích hình phẳng
26
Vận dụng: Thể tích khối trịn xoay cĩ liên quan hàm số chứa lnx
27
Thơng hiểu:Nguyên hàm của hàm số lượng giác
28
Thơng hiểu: Nguyên hàm của hàm số hữu tỷ
4. Số phức
29
Thơng hiểu: Tìm số phức dựa vào phếp tốn
30
Vận dụng: Tìm số phức thỏa mãn hai điều kiện cho trước, trong đĩ liên quan đến mơđun
31
Vận dụng: Tìm số phức thỏa mãn hai điều kiện cho trước, trong đĩ liên quan đến mơđun
32
Vận dụng: Tìm số phức thỏa mãn hai số phức bằng nhau và điều kiện phần thực nguyên
33
Nhận biết: Giải phương trình bậc hai trên tập hợp số phức
34
Nhận biết: Biểu diễn hình học của số phức
5. Khối đa diện
35
Thơng hiểu: Tính thể tích khối chĩp tam giác cĩ cạnh bên vuơng gĩc với đáy
36
Thơng hiểu: Tính thể tích khối chĩp tam giác cĩ mặt bên vuơng gĩc với đáy
37
Vận dụng: Tính thể tích khối chĩp tứ giác đều biết khoảng cách từ tâm đáy đến mặt bên
38
Vận dụng cao: Khối tứ diện đều liên quan đến phân chia, lắp ghép và dùng tỉ số thể tích
39
Vận dụng: Tính khoảng cách từ một điểm đến một mặt phẳng trong hình chĩp tứ giác
40
Thơng hiểu: Khối bát diện đều được tạo từ khối lập phương
41
Vận dụng cao: Dựa vào tỉ số thể tích xác định vị trí điểm sao cho mặt phẳng chia khối chĩp thành hai khối cĩ thể tích bằng nhau
6. Mặt nĩn – Mặt trụ - Mặt cầu
42
Vận dụng: Tính thể tích khối trịn xoay tạo thành khi hình bình hành quay xung quanh một cạnh của nĩ
43
Vận dụng: Sự tạo thành khối trụ từ một miếng tơn HCN theo các cách
7. Phương pháp tọa độ trong khơng gian
44
Thơng hiểu: Tìm điều kiện để ba điểm thẳng hàng
45
Thơng hiểu: Tìm điểm thuộc một đường thẳng thảo mãn về độ dài
46
Thơng hiểu: Viết phường trình mặt phẳng song song với một mặt phẳng và tiếp xúc với một mặt cầu
47
Nhận biết: Vị trí tương đối của hai đường thẳng
48
Nhận biết: Viết phương trình mặt phẳng dựa vào tích cĩ hướng của hai vectơ
49
Vận dụng: Tìm điểm M thuộc một đường thẳng sao cho diện tích tam giác MAB nhỏ nhất
50
Vận dụng: Viết phương trình mặt cầu cắt một phẳng theo một đường trịn cĩ chu vi xác định
ĐỀ THI THPT QG
Thời gian làm bài: 90 phút.
Câu 1: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Tỉ số bằng:
A. 	B. 	C. 	D. 
Câu 2: Đường cong hình vẽ dưới đây là đồ thị của hàm số nào sau đây
	A. 	B. 	C. 	D. 
Câu 3: Một tấm tơn hình chữ nhật cĩ kích thước 80cm x120cm. Người ta muốn làm một cái thùng khơng nắp, đáy là hình chữ nhật, bằng cách cắt bỏ 4 hình vuơng bằng nhau, mỗi hình vuơng cạnh là x (cm) tại 4 gĩc của tấm tơn, rồi gấp lên. Tìm x để hộp nhận được cĩ thể tích lớn nhất.
	A. cm	B. cm	C. cm	D. cm
Câu 4: Cho hàm số , hàm số đồng biến trên khoảng thì m là:
	A. 	B. 	C. 	D. 
Câu 5: Cho hai số thực x,y thỏa mãn . Giá trị nhỏ nhất của biểu thức bằng
	A. 	B. 	C. 	D. 3
Câu 6: Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là:
	A. 3	B. 1	C. 2	D. 4
Câu 7: Cho hàm số cĩ đồ thị . Viết phương trình tiếp tuyến của tại giao điểm của với trục tung.
A. 	B. 	C. 	D. 
Câu 8:Tìm tất cả các giá trị của tham số m để hàm số đạt cực tiểu tại .
A. hoặc 	B. 	C. 	D. 
Câu 9:Đường thẳng y = m cắt đồ thị hàm số tại 3 điểm phân biệt khi: 
A. B. C. D. 
Câu 10:Cho hàm số cĩ đạo hàm . Số điểm cực trị của hàm số là:
A. 0	B. 1	C. 2	D. 3
Câu 11: Cho hàm số cĩ đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị của m để phương trình cĩ ba nghiệm phân biệt là:
A. 	
B. 	
C. 	
D. 
Câu 12: Kết quả tính của biểu thức là:
	A. 	B. 	C. 	D. 
Câu 13: Phương trình cĩ nghiệm là:
	A. 	B. 	C. 	D. 
Câu 14: Tính đạo hàm của hàm số 
	A. 	B. 	C. 	D. 
Câu 15: Phương trình 
	A. Cĩ một nghiệm âm và một nghiệm dương
	B. Cĩ hai nghiệm dương
	C. Vơ nghiệm
	D. Cĩ hai nghiệm âm
Câu 16: Phương trình cĩ nghiệm là
	A. 	B. 	C. 	D. 
Câu 17: Phương trình cĩ nghiệm là:
	A. 	B. 	C. 	D. 
Câu 18: Ơng A vay ngân hàng 200 triệu đồng, với lãi xuất 14%/năm, kỳ hạn 3 tháng, thời gian vay là 9 tháng. Ơng A muốn cứ 3 tháng thì trả một phần số tiền cả gốc và lãi, 3 lần trả với số tiền bằng nhau.Hỏi theo cách đĩ thì số tiền T ơng A trả ngân hàng mỗi lần là bao nhiêu?
	A. (triệu đồng)	B. (triệu đồng)
	C. (triệu đồng)	D. (triệu đồng) 
Câu 19: Phương trình cĩ nghiệm là:
	A. 	B. 	C. 	D. Đáp án khác
Câu 20: Phương trình cĩ số nghiệm là:
	A. 3	B. 2	C. 0	D. 1
Câu 21: Tìm các giá trị của m để phương trình cĩ nghiệm.
	A. 	B. 	C. 	D. đúng với mọi m
Câu 22: Trong các đẳng thức, đẳng thức nào sai?
	A. 	B. 
	C. 	D. 
Câu 23: Cho hàm số liên tục trên , thỏa mãn và. Tính giá trị biểu thức
A. 
B. 
C. 
D.
Câu 24:Cho , đặt. Khẳng định nào sau đây đúng?
A. 
B. 
C. 
D. 
Câu 25: Cho hình phẳng giới hạn bởi đồ thị hàm số trục hồnh và các đường thẳng Tính diện tích của hình phẳng 
A. 
B. 
C. 
D. 
Câu 26: Cho hình phẳng giới hạn bởi đồ thị hàm số , trục hồnh và đường thẳng . Tính thể tích V của khối trịn xoay được tạo ra khi quay hình xung quanh trục Ox.
A. 
B. 
C. 
D. 
Câu 27: Nguyên hàm là?
	A. 	B. 	C. 	D. 
Câu 28: Tính nguyên hàm 
	A. 	B. 	C. 	D. 
Câu 29: Tìm số phức z, biết: .
A. 	B. 	C. 	D. 
Câu 30: Tìm số phức z biết và phần thực lớn hơn phần ảo một đơn vị.
A. , 	B. , 
C. , 	D. , 
Câu 31: Cho số phức z cĩ phần ảo gấp hai phần thực và . Khi đĩ mơ đun của z là:
A. 4	B. 6 	C. 	D. 
Câu 32: Cho z cĩ phần thực là số nguyên và .Tính mơđun của số phức: .
A. 	B. 	C. 	D. 
Câu 33: Trong C , Phương trình cĩ nghiệm là:
A. 	B. 	C. 	D. 
Câu 34: Gọi A là điểm biểu diễn của số phức z = 2 + 5i và B là điểm biểu diễn của số phức z’ = -2 + 5i. Tìm mệnh đề đúng trong các mệnh đề sau: 
A. Hai điểm A và B đối xứng với nhau qua trục hồnh
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x
Câu 35: Cho chĩp S.ABC cĩ SA (ABC) ,ABC vuơng cân tại B; BA=2a , gĩc giữa mặt phẳng (SBC) và (ABC) bằng .Thể tích khối chĩp S.ABC bằng :
	A. 	B. 	C. 	D. 
Câu 36: Cho hình chĩp tam giác S.ABC, đáy ABC là tam giác đều cạnh a, mặt bên SAB cũng là tam giác đều và nằm trong mặt phẳng vuơng gĩc với mặt phẳng đáy. Thể tích chối chĩp S.ABC là:
	A. 	B. 	C. 	D. 
Câu 37: Cho hình chĩp tứ giác đều S.ABCD, cĩ khoảng cách từ tâm đáy đến mặt bên bằng a. Mặt bên tạo với đáy một gĩc 600. Thể tích khối chĩp S.ABCD bằng :
	A. 	B. 	C. 	D. 
Câu 38:
Cho tứ diện đều ABCD cĩ cạnh bằng 8. Ở bốn đỉnh tứ diện, người ta cắt đi các tứ diện đều bằng nhau cĩ cạnh bằng , biết khối đa diện tạo thành sau khi cắt cĩ thể tích bằng thể tích tứ diện ABCD. Giá trị của là:
A.
B.
C.
D.
Câu 39: Cho hình chĩp cĩ đáy là hình thoi tâm cạnh Cạnh bên vuơng gĩc với đáy; gĩc giữa và mặt phẳng bằng Tính theo khoảng cách từ điểm đến mặt phẳng 
A. 
B. 
C. 
D. 
Câu 40:Người ta gọt một khối lập phương bằng gỗ để lấy khối tám mặt đều nội tiếp nĩ ( tức là khối cố các đỉnh là các tâm của các mặt khối lập phương). Biết cạnh của khối lập phương bằng. Hãy tính thể tích của khối tám mặt đều đĩ:
A. 	B. 	C. 	D. 
Câu 41: Cho hình chĩp cĩ đáy là hình vuơng cạnh , vuơng gĩc với mặt phẳng đáy và . Điểm M thuộc cạnh SA sao cho . Xác định k sao cho mặt phẳng chia khối chĩp thành hai phần cĩ thể tích bằng nhau.
A. 	B. 	C. 	D. 
Câu 42: Cho hình bình hành ABCD, cĩ AB=2a,AD=a, gĩc ABC=1200 ;quay hình bình hành xung quanh cạnh AD. Thể tích khối trịn xoay tạo thành là
	A. 	B. 	C. 	D. 
Câu 43: Từ một tấm tơn hình chữ nhật kích thước 50cm x 300cm, người ta làm các thùng đựng nước hình trụ cĩ chiều cao 50cm, theo hai cách sau (hình vẽ minh họa)
Cách 1: Gị tấm tơn ban đầu thành mặt xung quanh của 1 thùng.
Cách 2: Cắt tấm tơn ban đầu thành 3 tấm tơn bằng nhau, rồi gị mỗi tấm thành mặt xung quanh của một thùng.
Kí hiệu V1 là thể tích của thùng gị theo cách 1 và V2 là tổng thể tích cua 3 thùng gị theo cách 2. Tính tỉ số 
	A. 1	B. 2	C. 3	D. 4
Câu 44: Trong không gian Oxyz cho ba điểm Để ba điểm A, B, C thẳng hàng thì giá trị của 5x+y bằng : 
A. 36	B. 40	C. 42	D. 41
Câu 45:Trong khơng gian với hệ tọa độ Oxyzcho . Đường thẳng d đi qua A và vuơng gĩc với (P). Tìm tọa độ M thuộc d sao cho 
A.và ;	 B. và ;
C. và ;	D. và .
Câu 46: Trong khơng gian với hệ tọa độ Oxyzcho mặt cầu . Phương trình mặt phẳng (Q) song song với (P) và tiếp xúc với (S) là
A.x+2y -2z +25 = 0 và x+2y -2z + 1 = 0; B. x+2y -2z +31 = 0 và x+2y -2z – 5 = 0; 
C.x+2y -2z + 5 = 0 và x+2y -2z -31 = 0; D.x+2y -2z - 25 = 0 và x+2y -2z - 1 = 0.
Câu 47:Trong khơng gian với hệ tọa độ Oxyzcho . Vị trí tương đối của hai đường thẳng là
A. Song song;	B. Chéo nhau;	C. Cắt nhau;	D. Trùng nhau.
Câu 48:Trong khơng gian với hệ tọa độ Oxyzcho đường thẳng và (P) 
Mặt phẳng (Q) chứa đường thẳng d và vuơng gĩc mặt phẳng (P) cĩ phương trình 
A.;	B.	C.;	D..
Câu 49:Trong khơng gian với hệ tọa độ Oxyzcho A(1;5;0), B(3;3;6) và d:. Điểm M thuộc d để tam giác MAB cĩ diện tích nhỏ nhất cĩ tọa độ là
A. M(-1;1;0);	B.M(3;-1;4);	C.M(-3;2;-2);	D.M(1;0;2).
Câu 50: Trong khơng gian với hệ tọa độ Oxyzcho và đường thẳng , một phương trình mặt cầu cĩ tâm thuộc d tiếp xúc với (P) và cắt (Q) theo một đường trịn cĩ chu vi là
A.	;	B.;
C.;	D..