Đề thi học kì I, năm học: 2015 – 2016 môn: Toán; khối 9

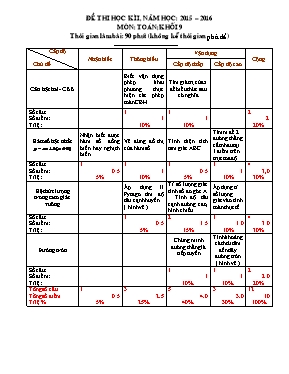
ĐỀ THI HỌC KÌ I, NĂM HỌC: 2015 – 2016
MÔN: TOÁN; KHỐI 9
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
 Cấp độ
 Chủ đề
Nhận biết
Thơng hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Căn bậc hai- CBB
Biết vận dụng phép khai phương thực hiện các phép tốn CBH	
Tìm giá trị của x để biểu thức sau cĩ nghĩa 
Số câu: 
Số điểm: 
Tỉ lệ: 
1
1
10%
1
1
10%
2
2
20%
Hàm số bậc nhất
Nhận biết được hàm số đồng biến hay nghịch biến. 
Vẽ đúng đồ thị của hàm số
Tính diện tích tam giác ABC
Tìm m để 2 đường thẳng cắt nhau tại 1 điểm trên trục toa độ
Số câu: 
Số điểm: 
Tỉ lệ: 
1
0.5
5%
1
1
10%
1
0.5
5%
1
1
10%
4
3,0
30%
Hệ thức lượng trong tam giác vuơng
Áp dụng lí Pytago tìm độ dài cạnh huyền.
( hình vẽ )
Tỉ số lượng giác tính số đo gĩc A . Tính độ dài cạnh đường cao, hình chiếu
Áp dụng tỉ số lượng giác vào tính tốn thực tế
Số câu: 
Số điểm: 
Tỉ lệ: 
1
0.5
5%
2
1.5
15%
1
1.0
10%
4
3.0
30%
Đường trịn
Chứng minh đường thẳng là tiếp tuyến
Tính khoảng cách từ tâm đến dây đường trịn
( hình vẽ )
Số câu: 
Số điểm: 
Tỉ lệ: 
1
1
10%
1
1
10%
2
2.0
20%
Tổng số câu
Tổng số điểm 
Tỉ lệ %
1
0.5
5%
3
2.5
25%
5
4.0
40%
3
3.0
30%
12
10
100%
Phịng giáo dục đào tạo Huyện Phú Tân ĐỀ THI HKI
Trường THCS BTĐ 	 Mơn Tốn 9
	 Thời gian 90 phút 
	 Năm học 2015 – 2016
Bài 1. (2 điểm) 
a).Rút gọn các biểu thức .
	b). Tìm giá trị của x để biểu thức cĩ nghĩa ? 
Bài 2. (3 điểm) 
 Cho hàm số bậc nhất và 
a). Hàm số đồng biến hay nghịch biến trên ? 
b). Vẽ đồ thị của hàm số và trên cùng mặt phẳng toạ độ Oxy. 
c) Hai đường thẳng và cắt nhau tại C, và lần lượt cắt trục Ox tại A và B. Hãy tính diện tích tam giác ABC .
d) Tìm m để đường thẳng y = 2x + m +1 cắt đường thẳng y = - x + 3 tại một điểm trên trục tung?. Tìm toạ độ điểm đĩ ?.
Bài 3. (3,0 điểm)
 Cho tam giác ABC vuơng tại B, cĩ đường cao BH, biết AB = 3cm; BC = 4cm.
a. Tính độ dài cạnh AC. 
b. Tính BH (kết quả làm trịn đến chữ số thập thứ hai ).
c. Tính số đo .
d. Dựng đường trịn tâm A, bán kính bằng 3 cm cắt tia BH tại D. Chứng minh CD là tiếp tuyến của đường trịn tâm A.
Bài 4: (1 điểm).
	Cho đường trịn tâm O, bán kính bằng 5cm và dây BC cĩ độ dài bằng 8 cm. Tính khoảng cách từ tâm đến dây BC.
Bài 5: (1 điểm)
Để chuẩn bị khai giảng năm học mới ở trường THCS Bình Thạnh Đơng, đồng chí bảo vệ kiểm tra cột cờ thì phát hiện dây kéo cờ bị hỏng nên phải thay dây mới. Để mua dây kéo cờ khơng bị thừa nên trường nhờ một giáo viên dạy tốn đo chiều cao cột cờ. Giáo viên khơng dùng thước đo chiều cao cột cờ mà dùng giác kế ngắm cột cờ với gĩc 36050’, chân giác kế cách cột cờ là 9,6 m. Vậy dây kéo cờ bao nhiêu mét. ( kết quả làm trịn đến chữ số thập phân thứ hai)
HẾT
III. HƯỚNG DẪN CHẤM MƠN TỐN - LỚP 9
Bài
Néi dung
Điểm
1
(2đ)
a) = 4.5 + 14: 7
 = 20 +7 
 = 27
0.5
0.25
0.25
Để cĩ nghĩa khi 4x +1 ³ 0
Nên 4x ³ -1
 Suy ra x ³ 
 Vậy cĩ nghĩa khi x ³ 
0.25
0.25
0.25 
0.25
2
(3đ)
a) Hàm số bậc nhất y = x + 1 đồng biến vì a = 1 > 0
 Hàm số bậc nhất y = - x + 3 nghịch biến vì a = -1 < 0
0,25
0,25
x
0
1
y = x +1
1
2
y = -x +3
3
2
 ( 0.5 điể )
Lưu ý : Vẽ thiếu ký hiệu x,y, điểm O hay mũi tên trừ 0.25 đ
0,5 điểm
1
c) Ta cĩ s = . CH. AB = . 2. 4
0,25
 S = 4 cm2
0.25
d) Đồ thị hàm số y = 2x + m + 1 cắt với đường thẳng y = -x + 3 khi và chỉ khi 
a a’ và b = b’ nên 2 -1 và m+1 = 3
 do đĩ m = 2
 Vậy m = 2 thì hai đường thẳng cắt nhau tại một điểm trên trục tung 
 Toạ độ giao điểm của hai điểm đĩ trên truc tung là ( 0; 3)
0.25
0.25
0.25
0.25
3
a
Áp dụng định lý Pytago vào tam giác vuơng ABC ta cĩ .
AC2 = AB2 + BC2
AC2 = 32 + 4 2
AC = 5 cm
Hình vẽ 0.5 điểm
0.25
0.25
b
Ta cĩ a.h = bc nên BH.AC = AB .BC 
Suy ra BH = (AB.BC) : AC
 BH = ( 3.4): 5 = 2,4 cm
0.25
0.25
C
Áp dụng tỉ số lượng giác vào tam giác vuơng ABC ta cĩ 
sinA = BC/AC = 4/5 
suy ra 
0.25
0.25
d
Xét hai tam giác ABC và ADC
Ta cĩ AB = AD = R
 ( vì ABD cân tại A, AH là đường cao cịn là đường phân giác )
 AC là cạnh chung
Nên ABC = ADC ( cgc)
Suy ra = 900 hay CD ^ AD tại D
Vậy CD là tiếp tuyến của đường trịn tậm B
0.25
0.25
0.25
0.25
4
1.5
 Ta cĩ BH = CH = 4 cm ( t/c đường kinh vuơng gĩc với dây )
Áp dung định lí Pytago vào tam giác vuơng OHB ta cĩ 
OH = vây Khoảng cách từ tâm đến dây đường trịn bằng 3 cm
Hình vẽ 0.25
0.25
0.25
0.25
5
Áp dụng tỉ số lượng giác vào tam giác vuơng ABC ta cĩ 
 tan ABC = => AC = AB tan ABC
AC = 9,6 tan 36050’ » 7,19 m
Vậy dây kéo cờ là 14,38m ( vì dây kéo cờ dài gấp 2 lần cột cờ )
0.25
0.25
0.25
0.25
Lưu ý: Học sinh cĩ thể giải cách khác nếu đúng thì vẫn cho điểm tối đa.
	Duyệt của BCM	Tổ trưởng	Giáo viên bộ mơn