Đề ôn tập Chương 1 môn Giải tích Lớp 12 - Đề 1 - Lê Ngọc Tuyến

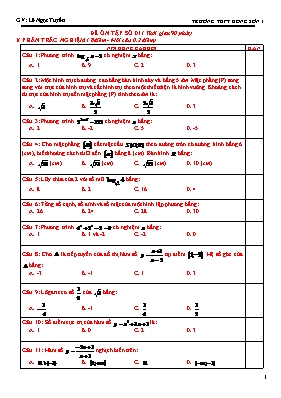
ĐỀ ÔN TẬP SỐ 01 ( Thời gian 90 phút)
I/ PHẦN TRẮC NGHIỆM ( 8điểm - Mỗi câu 0,2 điểm)
NỘI DUNG CÂU HỎI
Đ.ÁN
Câu 1: Phương trình có nghiệm bằng:
A. 1	B. 9	C. 2	D. 3
Câu 2: Một hình trụ có đường cao bằng bán kính đáy và bằng 5 dm. Mặt phẳng (P) song song với trục của hình trụ và cắt hình trụ theo một thiết diện là hình vuông. Khoảng cách từ trục của hình trụ đến mặt phẳng (P) tính theo dm là:
A. 	B. 	C. 	D. 3
Câu 3: Phương trình có nghiệm bằng:
A. 2	B. -2	C. 5	D. -5
Câu 4: Cho mặt phẳng cắt mặt cầu theo đường tròn có đường kính bằng 6 (cm), biết khoảng cách từ O đến bằng 8 (cm). Bán kính bằng:
A. (cm)	B. (cm)	C. (cm)	D. 10 (cm)
Câu 5: Lũy thừa của 2 với số mũ bằng:
A. 8	B. 2	C. 16	D. 4
Câu 6: Tổng số cạnh, số đỉnh và số mặt của một hình lập phương bằng:
A. 26	B. 24	C. 28	D. 30
Câu 7: Phương trình có nghiệm bằng:
A. 1	B. 1 và -2	C. -2	D. 0
Câu 8: Cho là tiếp tuyến của đồ thị hàm số tại điểm . Hệ số góc của bằng:
A. -3	B. -1	C. 1	D. 3
Câu 9: Lôgarit cơ số của bằng:
A. 	B. -1	C. 	D. 
Câu 10: Số điểm cực trị của hàm số là:
A. 1	B. 0	C. 2	D. 3
Câu 11: Hàm số nghịch biến trên:
A. 	B. 	C. 	D. 
Câu 12: Hàm số đồng biến trên khoảng:
A. 	B. 	C. 	D. 
Câu 13: Cho và . Khi đó:
A. và 	B. và 	C. và 	D. và 
Câu 14: Số điểm cực trị của hàm số là:
A. 2	B. 0	C. 1	D. 3
Câu 15: Cho hàm số có đồ thị là (F), hàm số có đồ thị là (G). Số giao điểm của (F) và (G) là:
A. 0	B. 2	C. 1	D. 3
Câu 16: Số đường tiệm cận của đồ thị hàm số là:
A. 1	B. 2	C. 0	D. 3
Câu 17: Cho khối trụ tròn xoay có bán kính mặt đáy bằng 2 (cm), chiều cao bằng 3 (cm). Thể tích của khối trụ tròn xoay này bằng:
A. (cm)	B. (cm)	C. (cm)	D. (cm)
Câu 18: Cho hình lập phương có cạnh bằng 1 cm. Thể tích của khối lập phương tính theo cm là:
A. 3	B. 4	C. 2	D. 1
Câu 19: Cho hình hộp MNPQ.M'N'P'Q' có thể tích bằng V; biết O, O' lần lượt là tâm của các hình bình hành MNPQ, M'N'P'Q'. Khối lăng trụ OMN.O'M'N' có thể tích bằng:
A. 	B. 	C. 	D. 
Câu 20: Giá trị viết dưới dạng lũy thừa là:
A. 	B. 	C. 	D. 
Câu 21: Hàm số đồng biến trên:
A. 	B. 	C. 	D. 
Câu 22: Hàm số có đạo hàm là:
A. 	B. 	C. 	D. 
Câu 23: Cho hình chóp tam giác đều có các cạnh đều bằng 3 cm. Thể tích của khối chóp tính theo cm là:
A. 3	B. 	C. 	D. 
Câu 24: Cho hình hộp chữ nhật có ba kích thước là 3cm, 4cm, 5cm. Thể tích của khối hộp chữ nhật tính theo cm là:
A. 20	B. 12	C. 15	D. 60
Câu 25: Cho hàm số . Khi đó:
A. 	B. 	C. 	D. 
Câu 26: Lôgarit cơ số 4 của bằng:
A. 	B. 	C. -2	D. 2
Câu 27: Lôgarit cơ số của () bằng:
A. 	B. 	C. 2	D. -2
Câu 28: Giá trị lớn nhất của hàm số trên đoạn bằng:
A. 0	B. 1	C. 5	D. 6
Câu 29: Tập xác định của hàm số là:
A. 	B. 	C. 	D. 
Câu 30: Tứ diện SABC có đáy là tam giác ABC vuông tại A, có SA(ABC) và SA=a, AB=b, AC=c. Mặt cầu đi qua các đỉnh A, B, C, S có bán kính bằng:
A. Một kết quả khác	B. 
C. 	D. 
Câu 31: Hàm số có đạo hàm là:
A. 	B. 
C. 	D. 
Câu 32: Lôgarit thập phân của 0,001 bằng:
A. 2	B. -2	C. 3	D. -3
Câu 33: Lôgarit cơ số 5 của 625 bằng:
A. -5	B. 5	C. 4	D. -4
Câu 34: Số mặt cầu chứa một đường tròn cho trước là:
A. 3	B. 1	C. 2	D. Vô số
Câu 35: Hàm số đạt cực đại tại điểm:
A. 	B. 	C. 	D. 
Câu 36: Lũy thừa của 3 với số mũ bằng:
A. 5	B. 1	C. 3	D. -5
Câu 37: Gọi I là tâm đối xứng của đồ thị hàm số . Điểm I có tọa độ là:
A. 	B. 	C. 	D. 
Câu 38: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 3 cm. Thể tích khối đa diện AB'CB tính theo cm là:
A. 60	B. 4,5	C. 15	D. 20
Câu 39: Giá trị của biểu thức bằng:
A. 	B. 	C. 	D. 
Câu 40: Lôgarit tự nhiên của bằng:
A. 2	B. 	C. 	D. -2
II/ PHẦN TỰ LUẬN
 Câu 1: ( 1,5 điểm)
 1.(0,75điểm). Giải hệ phương trình: 
 2.(0,75điểm). Tìm nguyên hàm : I =
 Câu 2: ( 0,5 điểm) 
 Cho hình chóp S.ABC có mặt đáy (ABC) là tam giác đều cạnh a. Chân đường vuông góc hạ từ S xuống mặt phẳng (ABC) là một điểm thuộc BC. Tính khoảng cách giữa hai đường thẳng BC và SA biết SA=a và SA tạo với mặt phẳng đáy một góc bằng 300.
HẾT
ĐÁP ÁN – TỰ LUẬN
Câu 1: (1 điểm) 1. x2 -3x(y-1) + y2 + y(x-3) = 0 (x-y)2 + 3(x-y) - 4 + 0 
* Với x- y = 1, ta có x = 1; y = 0 và x= -1; y = -2
* Với x - y = -4 ta có (Hệ PT vô nghiệm)
Vậy hệ phương trình có 2 nghiệm (x; y) = (1; 0) và (x; y) = (-1; -2)
Câu 1 :2. Tìm 
Đặt 1+cotx=t . Khi 
Vậy 
Câu 2
Gọi chân đường vuông góc hạ từ S xuống BC là H.
Xét DSHA(vuông tại H)
Mà DABC đều cạnh a, mà cạnh 
=> H là trung điểm của cạnh BC
=> AH ^ BC, mà SH ^ BC => BC^(SAH)
Từ H hạ đường vuông góc xuống SA tại K
=> HK là khoảng cách giữa BC và SA
=> 
Vậy khoảng cách giữa hai đường thẳng BC và SA bằng 
ĐỀ ÔN TẬP SỐ 01 ( Thời gian 90 phút)
Mỗi câu 0,25điểm
NỘI DUNG CÂU HỎI
Đ.ÁN
1
Câu 1: Phương trình có nghiệm bằng:
A. 1	B. 9	C. 2	D. 3
B
2
Câu 2: Một hình trụ có đường cao bằng bán kính đáy và bằng 5 dm. Mặt phẳng (P) song song với trục của hình trụ và cắt hình trụ theo một thiết diện là hình vuông. Khoảng cách từ trục của hình trụ đến mặt phẳng (P) tính theo dm là:
A. 	B. 	C. 	D. 3
3
Câu 3: Phương trình có nghiệm bằng:
A. 2	B. -2	C. 5	D. -5
B
4
Câu 4: Cho mặt phẳng cắt mặt cầu theo đường tròn có đường kính bằng 6 (cm), biết khoảng cách từ O đến bằng 8 (cm). Bán kính bằng:
A. (cm)	B. (cm)	C. (cm)	D. 10 (cm)
5
Câu 5: Lũy thừa của 2 với số mũ bằng:
A. 8	B. 2	C. 16	D. 4
C
6
Câu 6: Tổng số cạnh, số đỉnh và số mặt của một hình lập phương bằng:
A. 26	B. 24	C. 28	D. 30
C
7
Câu 7: Phương trình có nghiệm bằng:
A. 1	B. 1 và -2	C. -2	D. 0
D
8
Câu 8: Cho là tiếp tuyến của đồ thị hàm số tại điểm . Hệ số góc của bằng:
A. -3	B. -1	C. 1	D. 3
9
Câu 9: Lôgarit cơ số của bằng:
A. 	B. -1	C. 	D. 
B
10
Câu 10: Số điểm cực trị của hàm số là:
A. 1	B. 0	C. 2	D. 3
B
11
Câu 11: Hàm số nghịch biến trên:
A. 	B. 	C. 	D. 
A
12
Câu 12: Hàm số đồng biến trên khoảng:
A. 	B. 	C. 	D. 
B
13
Câu 13: Cho và . Khi đó:
A. và 	B. và 	C. và 	D. và 
14
Câu 14: Số điểm cực trị của hàm số là:
A. 2	B. 0	C. 1	D. 3
15
Câu 15: Cho hàm số có đồ thị là (F), hàm số có đồ thị là (G). Số giao điểm của (F) và (G) là:
A. 0	B. 2	C. 1	D. 3
16
Câu 16: Số đường tiệm cận của đồ thị hàm số là:
A. 1	B. 2	C. 0	D. 3
17
Câu 17: Cho khối trụ tròn xoay có bán kính mặt đáy bằng 2 (cm), chiều cao bằng 3 (cm). Thể tích của khối trụ tròn xoay này bằng:
A. (cm)	B. (cm)	C. (cm)	D. (cm)
18
Câu 18: Cho hình lập phương có cạnh bằng 1 cm. Thể tích của khối lập phương tính theo cm là:
A. 3	B. 4	C. 2	D. 1
19
Câu 19: Cho hình hộp MNPQ.M'N'P'Q' có thể tích bằng V; biết O, O' lần lượt là tâm của các hình bình hành MNPQ, M'N'P'Q'. Khối lăng trụ OMN.O'M'N' có thể tích bằng:
A. 	B. 	C. 	D. 
20
Câu 20: Giá trị viết dưới dạng lũy thừa là:
A. 	B. 	C. 	D. 
21
Câu 21: Hàm số đồng biến trên:
A. 	B. 	C. 	D. 
22
Câu 22: Hàm số có đạo hàm là:
A. 	B. 	C. 	D. 
23
Câu 23: Cho hình chóp tam giác đều có các cạnh đều bằng 3 cm. Thể tích của khối chóp tính theo cm là:
A. 3	B. 	C. 	D. 
24
Câu 24: Cho hình hộp chữ nhật có ba kích thước là 3cm, 4cm, 5cm. Thể tích của khối hộp chữ nhật tính theo cm là:
A. 20	B. 12	C. 15	D. 60
25
Câu 25: Cho hàm số . Khi đó:
A. 	B. 	C. 	D. 
26
Câu 26: Lôgarit cơ số 4 của bằng:
A. 	B. 	C. -2	D. 2
27
Câu 27: Lôgarit cơ số của () bằng:
A. 	B. 	C. 2	D. -2
28
Câu 28: Giá trị lớn nhất của hàm số trên đoạn bằng:
A. 0	B. 1	C. 5	D. 6
29
Câu 29: Tập xác định của hàm số là:
A. 	B. 	C. 	D. 
30
Câu 30: Tứ diện SABC có đáy là tam giác ABC vuông tại A, có SA(ABC) và SA=a, AB=b, AC=c. Mặt cầu đi qua các đỉnh A, B, C, S có bán kính bằng:
A. Một kết quả khác	B. 
C. 	D. 
31
Câu 31: Hàm số có đạo hàm là:
A. 	B. 
C. 	D. 
32
Câu 32: Lôgarit thập phân của 0,001 bằng:
A. 2	B. -2	C. 3	D. -3
33
Câu 33: Lôgarit cơ số 5 của 625 bằng:
A. -5	B. 5	C. 4	D. -4
34
Câu 34: Số mặt cầu chứa một đường tròn cho trước là:
A. 3	B. 1	C. 2	D. Vô số
D
35
Câu 35: Hàm số đạt cực đại tại điểm:
A. 	B. 	C. 	D. 
36
Câu 36: Lũy thừa của 3 với số mũ bằng:
A. 5	B. 1	C. 3	D. -5
37
Câu 37: Gọi I là tâm đối xứng của đồ thị hàm số . Điểm I có tọa độ là:
A. 	B. 	C. 	D. 
38
Câu 38: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 3 cm. Thể tích khối đa diện AB'CB tính theo cm là:
A. 60	B. 4,5	C. 15	D. 20
39
Câu 39: Giá trị của biểu thức bằng:
A. 	B. 	C. 	D. 
40
Câu 40: Lôgarit tự nhiên của bằng:
A. 2	B. 	C. 	D. -2
B
HẾT