Đề kiểm tra học kỳ I năm học 2013 – 2014 môn: Toán lớp 9 - Đề 8

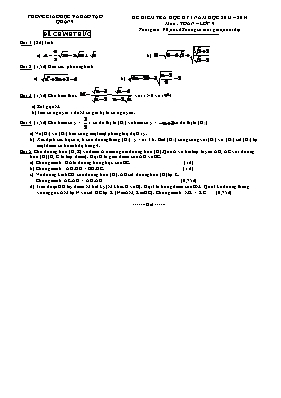
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO 
QUẬN 9
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2013 – 2014
Môn : TOÁN – LỚP 9
Thời gian: 90 phút (Không kể thời gian phát đề)
Bài 1: (2đ) Tính:	
	a) 	 b) 
Bài 2: (1,5đ) Giải các phương trình:
 a) b) 
Bài 3: (1,5đ) Cho biểu thức với x > 0 và x4	
 a) Rút gọn M.
 b) Tìm số nguyên x để M có giá trị là số nguyên.
Bài 4: (1,5đ) Cho hàm số y = x có đồ thị là (D1) và hàm số y = có đồ thị là (D2)	
Vẽ (D1) và (D2) trên cùng một mặt phẳng toạ độ Oxy.	
Xác định các hệ số a, b của đường thẳng (D3): y = ax + b. Biết (D3) song song với (D1) và (D3) cắt (D2) tại một điểm có hoành độ bằng 4. 
Bài 5: Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn (O). Qua A vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Gọi H là giao điểm của AO và BC. 
 a) Chứng minh: OA là đường trung trực của BC. (1 đ)
 b) Chứng minh: AH.HO = BH.HC. (1 đ)
 c) Vẽ đường kính CD của đường tròn (O). AD cắt đường tròn (O) tại E. 
 Chứng minh: AE.AD = AH.AO (0,75đ)
d) Trên đoạn OB lấy điểm M bất kỳ (M khác O và B). Gọi I là trung điểm của BM. Qua I kẻ đường thẳng vuông góc AM tại N và cắt OC tại K (NAM, KOC). Chứng minh: MK = KC (0,75đ)
------- Hết ------
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ I
Môn Toán lớp 9 - Năm học : 2013 – 2014
Bài 1: Tính:(2đ)	
a) 	 0,5 + 0,5
b) 	 0,5 +0,5
Bài 2: (1,5đ) Giải các phương trình:
a) 0,25 x 3
 Vậy S = 
b) ĐKXĐ: x 5 
 (thỏa ĐKXĐ) 0,25 x 3
Vậy S = 
Bài 3:(1,5đ) Cho với x > 0 và x4	
a) Rút gọn M: 
 0,5 + 0,5
b) Tìm số nguyên a để M có giá trị là số nguyên: 
M = nên M có giá trị là số nguyên khi Ư(2) = 0,25
 mà mặt khác x 4 
 Vậy x = 1 thì M có giá trị là số nguyên 0,25 
Bài 4: (1,5đ)	
a) Vẽ (D1) và (D2) trên cùng một mặt phẳng toạ độ Oxy. 
 Lập bảng giá trị đúng và vẽ đúng đồ thị (D1)	 	 0,25+0,25
 Lập bảng giá trị đúng và vẽ đúng đồ thị (D2) 	 0,25+0,25
b) (D3) // (D1) và b0 (D3): y = x + b 0,25 
Gọi A(4; y0) là giao điểm của (D3) và (D2)
A(4; y0) (D2) y0 = – 4 + 3 = – 1 A(4; –1)
A(4; –1) (D3) –1 = .4 + b b = – 3 0,25
Vậy (D3): y = x – 3
Bài 5: (3,5đ)
a) Chứng minh: OA là đường trung trực của BC.
 Ta có AB = AC (t/c 2 tiếp tuyến cắt nhau); OB = OC (bán kính)
AO là đường trực của BC 1
b) Chứng minh: AH.HO = BH.HC.
 Xét ABO vuông tại B có đường cao BH BH2 = AH.HO (hệ thức lượng) 0,5 
Mà BH = HC (AO là trung trực của BC BH.HC = AH.HO 0,5
c) Chứng minh: AE.AD = AH.AO
 CDE nội tiếp đường tròn đường kính CD CDE vuông tại E 
 Xét ACD vuông tại C có đường cao CE AC2 = AE.AD (hệ thức lượng) 0,25
 Xét ACO vuông tại C có đường cao CH AC2 = AH.AO (hệ thức lượng) 0,25
 AE.AD = AH.AO (= AC2) 0,25 
d) Chứng minh: MK = KC
 Áp dụng định lý Pythagore vào các tam vuông: ACK, ANK, MNK, IMN, ABI
Ta có CK2 = AK2 – AC2 
 = AN2 + NK2 – AB2 (vì AC = AB) 
 = AN2 + NK2 – (AI2 – BI2)
 = AN2 + NK2 – AI2 + IM2 (vì BI = IM)
 = AN2 + NK2 – (AN2 + NI2) + IM2 
 = AN2 + NK2 – AN2 – NI2 + IM2 
 = NK2 + MN2 ( vì MI2 – NI2 = MN2)
 = MK2
 Vậy CK = MK 0,75
 Học sinh có cách giải khác chính xác giáo viên cho trọn điểm