Đề kiểm tra chương I tiết 18 - Môn Đại số 9

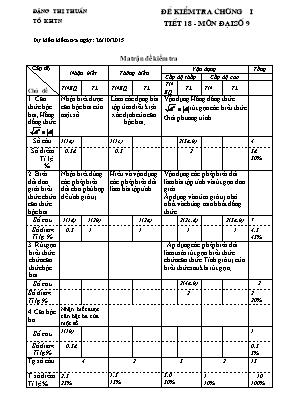
®Æng thÞ thuÇn
tæ khtn
®Ò kiÓm tra ch­¬ng i
tiÕt 18 - m«n ®¹i sè 9
Dự kiến kiểm tra ngày: 26/10/2015
Ma trận đề kiểm tra 
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TN
TL
1. Căn thức bậc hai, Hằng dẳng thức 
Nhận biết được căn bậc hai của một số
.
Làm các dạng bài tập tìm điều kiện xác định của căn bậc hai; 
Vận dụng Hằng dẳng thức 
 rút gọn các biểu thức
Giải phương trình 
Số câu
1(1a)
1(1c)
2(3a,b)
4
Số điểm Tỉ lệ %
0,5đ
 0,5
 2
3đ
30%
2. Biến đổi đơn giản biểu thức chứa căn thức bậc hai 
Nhận biết dùng các phép biến đổi cho phù hợp để tính giá trị 
Hiểu và vận dụng các phép biến đổi làm bài tập tính 
Vận dụng các phép biến đổi làm bài tập tính và rút gọn đơn giản
Áp dụng vào tìm giá trị nhỏ nhất và chứng minh bất đẳng thức 
Số câu
1(1d)
1(2b)
1(2a)
2(2c,d)
2(5a,b)
7
Số điểm Tỉ lệ %
0,5
 1
 1
1
1
4,5
45%
3. Rút gọn biểu thức chứa căn thức bậc hai
 Áp dụng các phép biến đổi làm toán rút gọn biểu thức chứa căn thức. Tính giá trị của biểu thức sau khi rút gọn;
Số câu
2(4a,b)
2
Số điểm 
Tỉ lệ % 
2
2
20%
4.Căn bậc ba
Nhận biết được căn bậc ba của một số 
Số câu
1(1b)
1
Số điểm Tỉ lệ %
 0,5đ
0,5
5%
Tg số câu
4
2
5
2
13
T số điểm Tỉ lệ %
2,5
25%
1,5
15%
5,0
50% 
1
10%
10 
100%
ĐỀ BÀI
C©u 1:(2 ®iÓm) Ghi l¹i c©u tr¶ lêi ®óng vµo bµi kiÓm tra:
 a, C¨n bËc hai sè häc cña 64 lµ: 	
A, 32	B, -32	C, 8	D, - 8
 b, C¨n bËc ba cña - 27 lµ:	
A. -3	B, 3	C, 9	D, 
 c, BiÓu thøc x¸c ®Þnh víi c¸c gi¸ trÞ: 
A, 	B, 	C, 	D, 
 d, §­a thõa sè vµo trong dÊu c¨n kÕt qu¶ nµo sau ®©y sai? 	
A. 	B, 	C, 	D, 
C©u 2:(3 ®iÓm) TÝnh: 
a, 	
b, 	
c, 	
d) 
Câu 3: (2 ®iÓm) Giải phương trình: 
	a) 	
b) 
Câu 4: (2 ®iÓm) 
Cho biểu thức: Với x > 0 , 	
	a) Rút gọn A
	b) Tìm giá trị của A khi
Câu 5: (1 ®iÓm) 
	a) Tìm giá trị nhỏ nhất của A = 
b) Chứng minh bất đẳng thức: (với a > c, b > c, c > 0)
IV. §¸p ¸n, biÓu ®iÓm:
Câu 1: (2 ®iÓm) Mỗi phần điền đúng được 0,5 điểm 
	Câu
a
b
c
d
Đáp án
C
A
B
C
Câu 2(3đ)
Đáp án
Biểu 
điểm
a(1đ)
0,5 đ
0,5 đ
b(1đ)
1 đ
c(0,5đ)
0,5 đ
d(0,5đ)
0,5 đ
Câu 3 (2đ)
a(1đ)
ĐK: : . 
Trả lời
0,75 đ
0,25 đ
b(1đ)
Trả lời
0,75 đ
0,25 đ
Câu 4(2đ)
a(1đ)
0,5 đ
0,5 đ
b(1đ)
Ta có: 
0,25 đ
0,75 đ
Câu 5 (1đ)
0,5đ
Có 
Nên . Vậy GTNN của A là -3 khi 
0,5 đ
0,5đ
Áp dụng bất đẳng thức Cô-si cho hai số không âm:
0,5 đ
®Æng thÞ thuÇn
tæ khtn
®Ò kiÓm tra ch­¬ng i
tiÕt 18 - m«n ®¹i sè 9
Dự kiến kiểm tra ngày: ..
Ma trận đề kiểm tra 
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TN
TL
1. Căn thức bậc hai, Hằng dẳng thức 
Nhận biết được căn bậc hai của một số
.
Làm các dạng bài tập tìm điều kiện xác định của căn bậc hai; 
Vận dụng Hằng dẳng thức 
 rút gọn các biểu thức
Giải phương trình 
Số câu
1(1a)
1(1c)
2(3a,b)
4
Số điểm Tỉ lệ %
0,5đ
 0,5
 2
3đ
30%
2. Biến đổi đơn giản biểu thức chứa căn thức bậc hai 
Nhận biết dùng các phép biến đổi cho phù hợp để tính giá trị 
Hiểu và vận dụng các phép biến đổi làm bài tập tính 
Vận dụng các phép biến đổi làm bài tập tính và rút gọn đơn giản
Áp dụng vào giải pt 
Số câu
1(1d)
1(2b)
1(2b)
1(c)
5
Số điểm Tỉ lệ %
0,5
 1
 1
1
3,5
35%
3. Rút gọn biểu thức chứa căn thức bậc hai
 Áp dụng các phép biến đổi làm toán rút gọn biểu thức chứa căn thức
Tính giá trị của biểu thức sau khi rút gọn;
Vận dụng hằng đẳng thức vào các biểu thức chứa ẩn đẻ giải phương trình nhiều biến 
Số câu
2(4a,b)
2(4c,5)
4
Số điểm 
Tỉ lẹ % 
1,5
1,5
3
30%
4.Căn bậc ba
Nhận biết được căn bậc ba của một số 
Số câu
1(1b)
1
Số điểm Tỉ lệ %
 0,5đ
0,5
5%
Tg số câu
4
4
5
2
14
T số điểm Tỉ lệ %
2,5
25%
1,5
15%
4,5
45% 
1,5
15%
10 
100%
§Ò bµi
C©u 1:(2 ®iÓm) Ghi l¹i c©u tr¶ lêi ®óng vµo bµi kiÓm tra:
 a, C¨n bËc hai sè häc cña 64 lµ: 	
A, 32	B, -32	C, 8	D, - 8
 b, C¨n bËc ba cña - 27 lµ:	
A. -3	B, 3	C, 9	D, 
 c, BiÓu thøc x¸c ®Þnh víi c¸c gi¸ trÞ: 
A, 	B, 	C, 	D, 
 d, §­a thõa sè vµo trong dÊu c¨n kÕt qu¶ nµo sau ®©y sai? 	
A. 	B, 	C, 	D, 
C©u 2:(3 ®iÓm) TÝnh: 
a, 	b, 	
c, 	d) 
Câu 3: (2 ®iÓm) Giải phương trình: 
	a) 	
b) 
Câu 4: (2 ®iÓm) Cho biểu thức: Với x > 0 , 	
	a) Rút gọn A
	b) Tìm giá trị của A khi
Câu 5: (1 ®iÓm) T ìm các số x, y, z biết:
IV. §¸p ¸n, biÓu ®iÓm:
Câu 1: (2 ®iÓm) Mỗi phần điền đúng được 0,5 điểm 
	Câu
a
b
c
d
Đáp án
C
A
B
C
Câu 2(3đ)
Đáp án
Biểu 
điểm
a(1đ)
0,5 đ
0,5 đ
b(1đ)
1 đ
c(0,5đ)
0,5 đ
d(0,5đ)
0,5 đ
Câu 3 (2đ)
a(1đ)
ĐK: : . Trả lời
0,25 đ
0,75 đ
b(1đ)
Trả lời
0,75 đ
0,25 đ
Câu 4(2đ)
a(1đ)
0,5 đ
0,5 đ
b(0,5đ)
Ta cã 
0,25 đ
0,25 đ
c(0,5đ)
b)
 ( vì x > 1). Vậy x > 9 thì .
0,25 đ
0,25 đ
Câu 5 (1đ)
(1đ)
Đ/K : x 0 ,y 1 ,z 2 
0,25 đ
0,25 đ
0,5 đ
ĐẶNG THỊ THUẦN
THCS CỘNG HOÀ
ĐỀ KSCL GIỮA HỌC KÌ I
MÔN: TOÁN 9
Thời gian: 90 phút.
Dự kiến kiểm tra ngày: ..
Ma trận 
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TN
TL
1. Căn thức bậc hai, Hằng dẳng thức 
Nhận biết được căn bậc hai của một số
.
Làm các dạng bài tập tìm điều kiện xác định của căn bậc hai; 
Vận dụng Hằng dẳng thức 
 rút gọn các biểu thức
Giải phương trình 
Số câu
1(1a)
1(1c)
2(3a,b)
4
Số điểm Tỉ lệ %
0,5đ
 0,5
 2
3đ
30%
2. Biến đổi đơn giản biểu thức chứa căn thức bậc hai 
Nhận biết dùng các phép biến đổi cho phù hợp để tính giá trị 
Hiểu và vận dụng các phép biến đổi làm bài tập tính 
Vận dụng các phép biến đổi làm bài tập tính và rút gọn đơn giản
Áp dụng vào giải pt 
Số câu
1(1d)
1(2b)
1(2b)
1(c)
5
Số điểm Tỉ lệ %
0,5
 1
 1
1
3,5
45%
3. Rút gọn biểu thức chứa căn thức bậc hai
 Áp dụng các phép biến đổi làm toán rút gọn biểu thức chứa căn thức
Tính giá trị của biểu thức sau khi rút gọn;
Vận dụng hằng đẳng thức vào các biểu thức chứa ẩn đẻ giải phương trình nhiều biến 
Số câu
2(4a,b)
2(4c,5)
4
Số điểm 
Tỉ lẹ % 
1,5
1,5
3
30%
4.Căn bậc ba
Nhận biết được căn bậc ba của một số 
Số câu
1(1b)
1
Số điểm Tỉ lệ %
 0,5đ
0,5
5%
Tg số câu
4
4
5
2
14
T số điểm Tỉ lệ %
2,5
25%
1,5
15%
4,5
45% 
1,5
15%
10 
100%
TRƯỜNG THCS CỘNG HOÀ
ĐỀ KHẢO SÁT CHẤT LƯỢNG GIỮA HỌC KÌ I
MÔN: TOÁN 9
Thời gian: 90 phút.
Câu 1: (2điểm) . Thực hiện các phép tính.
	a) 	b) 
	c) 	d) 
Câu 2: (1,5điểm) . Tìm x để:
	a) xác định	
b) 
	c) 
Câu 3: (2điểm) Cho biểu thức: Với x 0 , x ≠ 1
Rút gọn A.
Tìm giá trị của A khi .
Tìm x để A > 0.
Câu 4: (4điểm) 
1) Tìm chiều cao của cột cờ, biết bóng của cột cờ chiếu bởi ánh nắng mặt trời dài 12m và góc nhìn mặt trời là 380.( làm tròn đến chữ số thập phân thứ 2). 
2). Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành hai đoạn HB = 4cm, HC = 9cm. 
a) Tính AH, AB, AC. 
b) Tính sinB, sinC. 
c) Gọi D, E là hình chiếu của H trên AB và AC; M, N, O lần lượt là trung điểm của HB, HC, BC. Chứng minh: DM + EN = AO. 
Câu 5: (0,5điểm) 
Cho a, b, c là các số hữu tỉ đôi một khác nhau. Chứng minh: 
S = là số hữu tỉ.
---------------- HÕt -----------------
IV. ĐÁP ÁN, BIỂU ĐIỂM.
Câu 1(2đ)
Đáp án
Biểu 
điểm
a(0,5đ)
0,5 đ
b(0,5đ)
0,5 đ 
c(0,5đ)
0,5 đ
d (0,5đ)
0,5 đ
Câu 2 (1,5đ)
a(0,5đ)
 xác định khi 
0, 5 đ
b(0,5đ)
ĐK: : . Trả lời
0,5 đ
c(0,5đ)
Trả lời
0, 5 đ
Câu 3(2đ)
a(1đ)
0,5 đ
0,5 đ
b(0,5đ)
Ta có: 
0,25 đ
0,25 đ
c(0,5đ)
Để A > 0 thì: 
Vậy x > 4 thì A > 0.
0,5 đ
Câu 4 (4đ)
1(1đ)
A
Vẽ hình:
380
12 m
C
B
Gọi chiều cao của cột cờ là AB, bóng của nó là BC
Theo hệ thức giữa cạnh và góc ta có:
AB = BC. tanC
 = 12. tan 380 ...........
0,25 đ
0,25 đ
0,25 đ
0,25 đ
2(3đ) 
D
A
B
C
H
E
N
M
a) Vẽ hình: 
+ Ta có: BC = BH+HC = 4 + 9 =13
+ Áp dụng hệ thức giữa cạnh 
và đường cao ta có:
AH2 = HB.HC
0,25 đ
0,25 đ
0,25 đ
0,25 đ
b) Ta có: ;
0, 5 đ
0,5 đ
c) Ta có:
 BDH vuông tại D có DM là trung tuyến nên DM=BH/2
CEH vuông tại E có EN là trung tuyến nên EN=CH/2.
ABC vuông tại A có AO là trung tuyến nên AO=BC/2 
Mà BH/2+CH/2 = BC/2
Nên ta có: DM + EN = AO
0,25 đ
0,25 đ
0,25 đ
0,25 đ
Câu 5: (0,5điểm)
Ta có: 
Đặt x = a – b; y = b – c; z = c – a thì x + y + z = 0
 Suy ra: 
Vậy S = 
Vì a, b, c là các số hữu tỉ đôi một khác nhau. Nên S là số hữu tỉ.
0,25 đ
0,25 đ
ĐẶNG THỊ THUẦN
THCS CỘNG HOÀ
ĐỀ KIỂM TRA CHƯƠNG I HÌNH HỌC 9
Thời gian: 45 phút.
TIẾT 19
DỰ KIẾN KIỂM TRA VÀO THỨ 2 NGÀY 27/10/2014
Thiết kế ma trận 
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Hệ thức lượng trong tam giác vuông 
Vẽ được hình đúng
Biết vận dụng hệ thức vào tính độ dài đoạn thẳng và chứng minh hệ thức 
Số câu
1
2
1
4
Số điểm Tỉ lệ %
0,5đ
1,5đ
1
3
30%
Tỉ số lượng giác của góc nhọn 
Nhận biết và hiểu được tỉ số lượng giác của góc nhọn để tính đoạn thẳng, tính góc 
Số câu
2
1
3
Số điểm Tỉ lệ %
1đ
 1,5đ
2,5
25%
Hệ thức giữa cạnh và góc trong tam giác vuông 
Nắm vững hệ thức giữa cạnh và góc vận dụng vào giải tam giác. Vận dụng vào tính chiều cao của vật 
Vận dung giải được tam giác 
Số câu
2
1
1
1
5
Số điểm Tỉ lệ %
1đ
	1,5đ
 1đ
1đ
4,5
45%
Tổng số câu
5
2
3
2
	2
20%
12
Tổng số điểm Tỉ lệ %
2,5
25% 
3
30%
2,5
25% 
10 100%
ĐỀ KIỂM TRA CHƯƠNG I
M
N
P
(Thời gian làm bài 45 phút )
I. Phần trắc nghiệm ( 2 điểm ) 
Câu 1:(1điểm). Cho hình vẽ. Điền vào chỗ () cho đúng. . 
	MN =  sinP =  cosN
	 = .. tanP =  cotN
Câu 2: (1điểm). Câu trả lời đúng là: 
Cho hình vẽ bên: 
 a) Sina bằng
 A. ; B. ; C. D. 
b) cotb bằng:
 A. ; B. ; C. D.
Câu 3: (3 điểm). 
Dựng góc nhọn biết tan = . 
Tính chiều cao của một cây biết bóng của nó trên mặt đất dài 6,5m và góc tạo bởi tia nắng mặt trời với mặt đất tại thời điểm đó là 400.
Câu 4: (3 điểm ). Cho ABC vuông tại A, có AB = 6cm, BC = 10cm, đường cao AH.
Tính AC, AH
Gọi M,N lần lượt là hình chiếu của H trên AB và AC. 
 Chứng minh rằng AN.AC =AM.AB
Câu 5: (2điểm ) Giải tam giác ABC trong các trường hợp sau:
	a) = 900, , BC = 12cm.
	b) BC = 40; ; 
Đáp án và biểu điểm
Câu
Nội dung
Biểu điểm
Phần trắc nghiệm :2điểm 
 1
Mỗi ý đúng cho 0,25 đ: MN.MN, MPMP.
1 đ
 2
Mỗi ý đúng cho 0,5đ a - C b, - A
1 đ
Phần tự luận (8điểm )
3
( 3đ) 
a)+ Dựng góc vuông xOy 
+ Lấy một đoạn thẳng làm đơn vị
+ Trên Ox lấy điểm A sao cho
 OA = 2 đơn vị .
+ Trên Oy lấy điểm B sao cho 
OB = 5 đv
+ Nối A với B Ta có = 
Thật vậy, tan = 
Vẽ hình đúng.
0,5đ
0,5đ
b) Gọi các điểm, để có tam giác vuông
Áp dụng hệ thức tính chiều cao của cây
Chiều cao của cây gần bằng ..: 
0,5 đ
1 đ
0,5đ
4
(3đ)
a) Vẽ hình
a) Tính AC nhờ định lí Pytago được AC = 8cm.
Tính AH nhờ hệ thức 3: được AH = 4,8cm 
Theo hệ thức lượng trong tam giác vuông 
=> AH = AN .AC
 AH = AM .AB
 => AM.AB =AN .AC
0,5đ
0,75đ
0,75đ
1đ
5
(2đ)
a) Ta có: 
Áp dụng hệ thức giữa cạnh và góc trong tam giác ta có:
AB = BC.sin C = 12. sin 480 
AC = BC.sin B = 12.sin520 
Trả lời
0,25đ
0,25đ
0,25đ
0,25đ
b) Kẻ BK vuông góc với AC, áp dụng hệ thức giữa cạnh và góc trong tam giác BKC ta có: BK = BC. Sin C= 40.sin350 
Có: góc BAK = 400 + 350 = 750 (tính chất góc ngoài của tam giác) 
Trong tam giác ABK có: sinA1 = 
Kẻ AH vuông góc với BC, trong tam giác AHB có:
AH = AB.sinB 
Trong tam giác AHC có sinC = 
0,25đ
0,25đ
0,25đ
0,25đ
Ma trËn ®Ò kiÓm tra ch­¬ng II - ®¹i sè 9- tiÕt 30
Néi dung
NhËn biÕt
Th«ng hiÓu
VËn dông
Tæng
CÊp ®é thÊp
CÊp ®é cao
Kh¸i niÖm hµm sè. Hµm sè 
y = a x +b (a 0)
Sè c©u
Sè ®iÓm
TØ lÖ %
Biết xác định c¸c tÝnh: ®ång biÕn, nghÞch biÕn cña hµm sè bËc nhÊt cụ thể. 
BiÕt ®å thÞ hµm sè c¾t trôc tung t¹i tung ®é gèc b. Biết điểm thuộc hay không thuộc đồ thị của hàm số
3 c©u
1,5 ®iÓm
15%
- VÏ ®óng ®å thÞ c¸c hµm sè bËc nhÊt.
1 c©u
2 ®iÓm
20%
- T×m ®­îc gi¸ trÞ a hoÆc b khi biÕt hai gi¸ trÞ t­¬ng øng cña x vµ y vµ hÖ sè b(hoÆc a)
2 c©u
2 ®iÓm
20%
- VËn dông t×m ®­îc khoảng cách từ gốc toạ độ đến 1 đường thẳng là lớn nhất 
1 c©u
1 ®iÓm
10%
7 c©u
6,5®iÓm
65%
HÖ sè gãc cña ®­êng th¼ng. Hai ®­êng th¼ng song song, hai ®­êng th¼ng c¾t nhau.
Sè c©u
Sè ®iÓm
TØ lÖ %
BiÕt hÖ sè gãc cña mét ®­êng th¼ng
1 c©u
0,5 ®iÓm
5%
- VËn dông vÞ trÝ t­¬ng ®èi cña hai ®­êng th¼ng y = ax +b (a 0); y = a’x + b’(a’0) t×m tham sè ®Ó cã vÞ trÝ song song hoÆc c¾t nhau.
1 c©u
1 ®iÓm
10% 
- Tìm giá trị của tham số để các đường thẳng đồng quy, cắt nhau tại một điểm đặc biệt.
2 c©u
2 ®iÓm
20%
4 c©u
3,5®iÓm
35%
Tæng
4 c©u
2 ®iÓm
20%
1 c©u
2 ®iÓm
20%
3 c©u 
3 ®iÓm
30%
3 c©u
3 ®iÓm
30%
11 c©u
10 ®iÓm
Đề bài:
Câu 1:(2 điểm) Điền vào chỗ (...) cho thích hợp: Cho hàm số: y = 2x - 5
a, Hàm số có hệ số góc là: ........
 	b, Hàm số có tính chất: ................................. vì có a .... 0 
c, Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng : ..
d, Trong các điểm: A(-2; -1), B(3;2), C(4;4), D(1;- 3) điểm thuộc đồ thị hàm số là: .
Câu 2:(2 điểm) 
Cho hàm số y = ax – 4. Tìm hệ số a, biết khi x = 3 thì y = 2.
Cho hàm số y = - 2x + b. Xác định hệ số b trong trường hợp (d) đi qua A(1; 3)
Câu 3:(6 điểm) Cho ba hàm số: y = 2x (d1); y = - x +3 (d2) và y = mx + m + 1 (d3) 
Vẽ trên cùng mặt phẳng toạ độ đồ thị (d1) và (d2) 
Tìm m để (d3) song song với (d1).
Tìm m để ba đường thẳng đồng quy.
Tìm m để (d3) cắt (d2) tại một điểm nằm bên phải trục tung.
Tìm m để khoảng cách từ gốc toạ độ đến (d3) là lớn nhất. 
Đáp án + biểu điểm
Câu
Đáp án
Điểm
Câu1 :(2 đ) Mỗi phần đúng được 0,5 điểm
a, a = 2
b,  đồng biến  a > 0
c, ..... -5
d, C(1; -3)
0,5 đ
0,5 đ
0,5 đ
0,5 đ
Câu2 :(2 đ) 
Thay x = 3, y = 2 vào công thức y = ax – 4 ta có:
2 = a.3 – 4 ó . ó a = 2. Trả lời
b) Đồ thị (d) qua A( 1;3) có nghĩa: x = 1; y = 3 
+ thay vào công thức hàm số y = - 2x + b ta được:
3 = -2.1 + b b = 2 + 3 = 5. Trả lời
0,5 đ
0,5 đ
0,5 đ
0,5 đ
Câu3 :(6 đ) Phần a đúng được 2 điểm
Các phần còn lại mỗi phần đúng được 1 điểm
a) Xác địng điểm đúng
Vẽ đúng đồ thị 
2, đ
Để (d3) song song với (d1) tời:
Trả lời
1,0 đ
Hoành độ giao điểm là nghiệm của phương trình:
- x + 3 = 2x ó 3x = 3 ó x = 1
Tung độ giao điểm là : y = 2.1 = 2
Toạ độ giao điểm là (1; 2).
Để ba đường thẳng đồng quy thì (d3) đi qua A(1;2).
 Thay x = 1; y = 2 vào (d3) y = mx + m + 1 ta được:
2 = m + m + 1ó.... ó m = -1/2.
Trả lời:... 
0,5 đ
0,25 đ
0,25 đ
 Hoành độ giao điểm là nghiệm của phương trình:
- x + 3 = mx + m + 1ó  ó 
Để (d3) cắt (d2) tại một điểm nằm bên phải trục tung thì x > 0
Trả lời
Gọi điểm cố định mà (d3) luôn đi qua với mọi m là: (x0;y0) suy ra: x = x0 ; y = y0 ta có:
 y0 = mx0 + m + 1 
 ó y0 = m x0 + m + 1 
 ó y0– 1 = m (x0 +1) 
Vậy điểm cố định mà (d3) luôn đi qua là: M(-1;1)Ta có:
OM = .
Kẻ OH(d3) ta có OH 
Gọi A và B là giao của (d3) với 2 trục toạ độ. Ta có: 
A(0;m+1) => OA = 
B
 Theo hệ thức giữa cạnh và góc trong tam giác OAB đường cao OH ta có: 
Vậy với m = 1 thì khoảng cách từ gốc toạ độ đến (d3) là lớn nhất là 
0,25 đ
0,5 đ
0,25 đ
0,25 đ
0,5 đ
0,25 đ