Đề kiểm tra chương I – Đại số 7 (tiết 22)

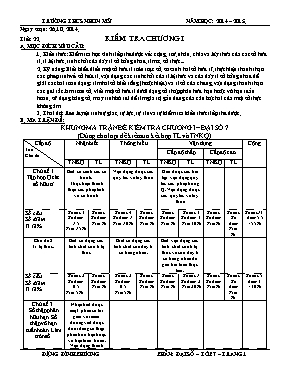
Ngày soạn: 26. 10. 2014.
Tiết: 22. 	KIỂM TRA CHƯƠNG I
A. MỤC ĐÍCH YÊU CẦU:
1. Kiến thức: Kiểm tra học sinh tiếp thu được về: cộng, trừ, nhân, chia và lũy thứa của các số hữu tỉ, tỉ lệ thức, tính chất của dãy tỉ số bằng nhau, tìm x, số thực  
2. Kỹ năng: Biết biểu diễn một số hữu tỉ trên trục số, so sánh hai số hữu tĩ, thực hiện thành thạo các phép tính về số hũu tỉ, vận dụng các tính chất của tỉ lệ thức và của dãy tỉ số bằng nhau để giải các bài toán dạng: tìm hai số biết tổng (hoặc hiệu) và tỉ số của chúng, vận dụng thành thạo các qui tắc làm tròn số, viết một số hữu tỉ dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn, sử dụng bảng số, máy tính bỏ túi để tìm giá trị gần đúng của căn bậc hai của một số thực không âm
3. Thái độ: Rèn luyện tính tự giác, tự lực, tự tin và tự kiểm tra kiến thức tiếp thu được.
B. MA TRẬN ĐỀ:
KHUNG MA TRẬN ĐỀ KIỂM TRA CHƯƠNG I – ĐẠI SỐ 7 
(Dùng cho loại đề kiểm tra kết hợp TL và TNKQ)
 Cấp độ
Tên 
Chủ đề 
Nhận biết
Thơng hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Chủ đề 1 
Tập hợp Q các số hữu tỉ
Biết so sánh các số hữu tỉ.
Thực hiện thành thạo các phép tính về số hữu tỉ
Vận dụng được các quy tắc về luỹ thừa 
Giải được các bài tập vận dụng quy tắc các phép trong Q. Vận dụng được các quy tắc về luỹ thừa 
Số câu 
Số điểm 
Tỉ lệ %
Số câu 3 
Số điểm 1,5
Tỉ lệ 15%
Số câu
Số điểm
Tỉ lệ %
Số câu 4
Số điểm 1
Tỉ lệ 10 %
Số câu
Số điểm
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu 3
Số điểm 3 
Tỉ lệ 30%
Số câu
Số điểm
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu13
 điểm 5,5
=55% 
Chủ đề 2
Tỉ lệ thức.
Biết sử dụng các tính chất của tỉ lệ thức
Biết sử dụng các tính chất của dãy tỉ số bằng nhau.
Biết vận dụng các tính chất của tỉ lệ thức và của dãy tỉ số bằng nhau để giải bài tốn thực tiễn.
Số câu 
Số điểm 
Tỉ lệ %
Số câu 2 
Số điểm 0,5 
Tỉ lệ 5%
Số câu 
Số điểm 
Tỉ lệ %
Số câu 2
Số điểm 0,5
Tỉ lệ 5%
Số câu
Số điểm
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu 1 
Số điểm 2
Tỉ lệ 20%
Số câu
Số điểm
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu 5 
điểm 3
=30 % 
Chủ đề 3.
Số thập phân hữu hạn. Số thập vơ hạn tuần hồn. Làm trịn số.
Nhận biết được một phân số tối giản với mẫu dương viết được dưới dang số thập phân hữu hạn hoặc vơ hạn tuần hồn. Vận dụng thành thạo các quy tắc làm trịn số
Số câu 
Số điểm 
Tỉ lệ %
Số câu 2 
Số điểm 0,5 
Tỉ lệ 5%
Số câu
Số điểm
Tỉ lệ %
Số câu 
Số điểm 
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu 
Số điểm 
Tỉ lệ %
Số câu 
Số điểm 
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu 
Số điểm
Tỉ lệ %
Số câu 2
 điểm 0,5
=5% 
Chủ đề 4.
Tập hợp số thực R
Biết cách viết một số hữu tỉ dưới dạng số thập phân hữu hạn hoặc vơ hạn tuần hồn
Biết được rằng tập hợp số thực bao gồm tất cả số hữu tỉ và số vơ tỉ
Số câu 
Số điểm 
Tỉ lệ %
Số câu 2 
Số điểm 0,5 
Tỉ lệ 5 %
Số câu
Số điểm
Tỉ lệ %
Số câu 2
Số điểm 0,5
Tỉ lệ 5%
Số câu
Số điểm
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu
Số điểm
Tỉ lệ %
Số câu 4
Số điểm 1
= 10%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
Số câu 12
Số điểm 3
30%
Số câu 8
Số điểm 2
20%
Số câu 4
Số điểm 5
50%
Số câu 25 
Số điểm 10
100% 
C. ĐỀ KIỂM TRA:
Câu 1. Trong các số hữu tỉ số hữu tỉ lớn nhất là: 
Câu 2. Kết qủa của phép tính bằng:
Câu 3. Kết qủa của phép tính bằng:
Câu 4. Từ đẳng thức: ta suy ra được tỉ lệ thức nào?
Câu 5. Phân số nào viết được dưới dạng số thập phân vơ hạn thuần hồn?
Câu 6. Làm trịn số đến hàng phần trăm ta được: 
Câu 7. Nếu thì x = 
 . Điền dấu X vào ô thích hợp 
Nối mỗi dòng ở cột trái với một dòng ở cột phải để được khẳng định đúng.
Bài 1 (0,75 điểm) Thực hiện phép tính sau: 
Bài 2 (0,75 điểm) Tìm x biết: 
Bài 3 (2 điểm) Nhà trường đề ra chỉ tiêu phấn đấu của học kỳ I đối với học sinh khối 7 là số học sinh giỏi, khá, trung bình, yếu của khối tỷ lệ với 9; 11; 13; 3; khơng cĩ học sinh kém. Hỏi theo chỉ tiêu của nhà trường thì cĩ bao nhiêu học sinh giỏi, khá, trung bình, yếu? Biết rằng số học sinh khá nhiều hơn số học sinh giỏi là 20 em.
Bài 4 (0,75 điểm) Trong hai số sau: và , số nào lơn hơn giải thích ?
Bài 5 (0,75 điểm) Chứng minh rằng: chia hết cho 14.
D. ĐÁP ÁN, BIỂU ĐIỂM:
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp án
A
A
A
B
B
C
B
A
B
Đ 
S 
Đ
2
A+3
B+1
C+4
D+2
BÀI
NỘI DUNG
ĐIỂM
1
0,75 điểm
0,25
0,25 
0,25
2
0,75 điểm
Hoặc 
Vậy : x = 4 hoặc x = 2
3
2 điểm
Gọi số học sinh giỏi khá trung bình, yếu của khối 7 lần lượt là; x, y, z, t 
Ta cĩ: và 
Vậy: 
Số học sinh giỏi khá trung bình, yếu của khối 7 lần lượt là; 90; 110; 130; 30
4
0,75 điểm
Ta cĩ: 
Và 
5
0,75 điểm
Ta cĩ: 
Vậy chia hết cho 14
E. KẾT QUẢ (thống kê các loại điểm, tỉ lệ)
LỚP
SĨ SỐ
GIỎI
KHÁ
TRUNG BÌNH
YẾU
KÉM
ĐAT YC
SL
%
SL
%
SL
%
SL
%
SL
%
SL
%
7A1
42/24
7A2
45/15
TỔNG CỘNG
87/39
G. NHẬN XÉT, RÚT KINH NGHIỆM (sau khi chấm bài xong).