Đề kiểm tra 15 phút Hình học 12

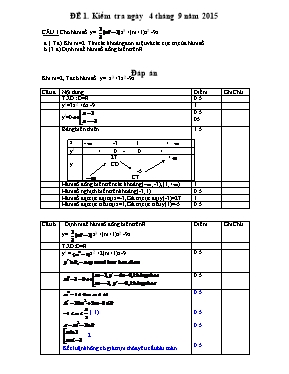
ĐỀ 1. Kiểm tra ngày 4 tháng 9 năm 2015
CÂU 1 Cho hàm số y= x3 +(m+1)x2 -9x
 a. ( 7 đ). Khi m=2. Tìm các khoảng đơn điệu và các cực trị của hàm số.
 b.( 3 đ) Định m để hàm số đồng biến trên R.
Đáp án
Khi m=2, Ta có hàm số y= x3 +3x2 -9x
Câu a
Nội dung
Điểm
Ghi Chú
TXĐ : D=R
0.5
y/ =3x2 +6x -9
1
y/=0
0.5
05
Bảng biến thiên
x
- -3 1 +
y/
 + 0 - 0 +
y
 27 +
 CD
 -5 
 CT 
1.5
Hàm số đồng biến trên các khoảng (-;-3), (1;+)
1
Hàm số nghịch biến trên khoảng (-3;1)
0.5
Hàm số đạt cực đại tại x=-3,Giá trị cực đại y(-3)=27 
1
Hàm số đạt cực tiểu tại x=1,Giá trị cực tiểu y(1)=-5 
0.5
Câu b
 Định m để hàm số đồng biến trên R.
y= x3 +(m+1)x2 -9x
Điểm 
Ghi Chú
TXĐ:D=R
y/ =x2 +2(m+1)x -9
0.5
0.5
 ( 1)
 2 
 Kết luận không có giá trị m thỏa yêu cầu bài toán. 
0.5
0.5
0.5
0.5
ĐỀ 2 Kiểm tra ngày 25 tháng 9 năm 2015
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SB vuông góc với đáy, cạnh bên SD tạo với đáy một góc 450 .
 a. Tính thể tích hình chóp.
 b. Tính khoảng cách từ A đến mp(SCD).
 ĐÁP ÁN.
Câu
Đáp án
Điểm
Hình vẽ
 S
 B C
 A D
1 đ
a.
Do SB mp (ABCD), nên SB là đường cao của hình chóp.
BD là hình chiếu vuông góc của cạnh bên SD trên đáy và góc SDB bằng 450
0.5 đ
1 đ
Thể tích của khối chóp là V= dtABCD.h
0.5 đ
Trong đó dt ABCD=(2a)2 =4a3, 
BD=, 
vì tam giác SBD vuông cân tại B. Nên h=SB=BD= 
Vậy thể tích cần tính V
1đ
1 đ 
1 đ
1 đ
b.
Ta có AB//CD, suy ra AB//mp(SCD). Vậy khoảng cách từ A đến mp(SCD) bằng khoảng cách từ B đến mp(SCD).
Gọi I là hình chiếc của B trên SC, ta có BI SC.
Vì SB mp(ABCD) và DCBC, suy ra CDBI, suy ra BImp(SCD).
Vậy khoảng cách từ B đến mp(SCD) bằng BI.
BI là đường cao của tam giác vuông SBC, vuông tại B nên 
 đó là khoảng cách cần tính.
1đ
1 đ
1 đ
ĐỀ 1 Kiểm tra một tiết ngày 09 tháng 10 năm 2015
 Cho hình lăng trụ đứng ABCD.A/ B/C/D/ , có đáy ABCD là hình chữ nhật. Biết cạnh AD=a, đường chéo AC=a, góc A/ AD=450 
 1.(2đ) Tính diện tích ABCD.
 2. (3đ) Tính thể tích khối lăng trụ đứng ABCD.A/ B/C/D/.
 3. (2 đ) Xác định và tính góc giữa đường thẳng A/ C và mặt phẳng (ABCD).
 4. (2 đ)Tính khoảng cách từ B đến mp(A/CD).
 5. (1 đ)Mặt phẳng (A/CD) chia khối lăng trụ thành hai khối đa diện. Tính tỷ số thể tích hai khối đó.
 ĐÁP ÁN.
Câu
Đáp án
Điểm
 A/ B/
 D/ C/
 H
 A B
	D C
1 đ
1.
Tam giác ADC vuông tại D nên DC2=AC2-AD2=(a)2-a2=2a2 
Vậy diện tích ABCD=AD.CD=a.a
0.5 đ
0.5 đ
0.5+0.5
2
Ta có , nên AA/=h là đường cao của lăng trụ đã cho. Tam giác A/AD vuông cân tại A nên AA/=AD=a. ( vì góc ADA=450)
Thể tích của khối lăng trụ là V= dtABCD.h=
0.5 
1
1+0.5
3
Ta có , nên AC là hình chiếu của A/C trên mp(ABCD)
Vậy góc giữa đường thẳng A/C với mp(ABCD) là góc A/CA
Trong tam giác vuông A/AC vuông tại A ta có tanA/CA
0.5
0.5 
1 đ
4
Ta có AB//CD, suy ra AB//mp(A/CD). Vậy khoảng cách từ B đến mp(A/CD) bằng khoảng cách từ A đến mp(SCD).
Gọi H là hình chiếc của A trên A/D, ta có AH A/D.
Vì A/A mp(ABCD) và DCAD, suy ra CDAH, suy ra AHmp(A/CD).
Vậy khoảng cách từ A đến mp(A/CD) bằng AH.
AH là đường cao của tam giác vuông cân A/AD, vuông tại A nên 
 đó là khoảng cách cần tính.
0.5
0.5
1 đ
5
Ta có mp(A/CD) cắt khối lăng trụ theo thiết diện là A/B/CD .
 Ta có hai khối đa diện đối xứng nhau qua mp(A/B/CD) .
Vậy tỷ số thể tích hai khối cần tính bằng 1
0.25
0.25
0.5
 A/ B/
 D/ CCCCCCCCCC
 A
 AA B
	D C