Đại số 8 - Chương 3: Phương trình bậc nhất một ẩn

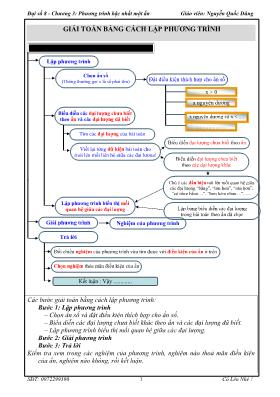
Đại số 8 - Chương 3: Phương trình bậc nhất một ẩn Giáo viên: Nguyễn Quốc Dũng 
SĐT: 0972299390 Cố Lên Nhé ! 
1
 GIẢI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH 
` 
Các bước giải toán bằng cách lập phương trình: 
 Bước 1: Lập phương trình 
 – Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. 
 – Biểu diễn các đại lượng chưa biết khác theo ẩn và các đại lượng đã biết. 
 – Lập phương trình biểu thị mối quan hệ giữa các đại lượng. 
 Bước 2: Giải phương trình 
 Bước 3: Trả lời 
Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện 
của ẩn, nghiệm nào không, rồi kết luận. 
Lập phương trình 
x nguyên dương và x < .... 
Giải phương trình 
trình 
Nghiệm của phương trình 
trình 
Chọn ẩn số 
(Thông thường gọi x là số phải tìm) 
) 
Đặt điều kiện thích hợp cho ẩn số 
x > 0 
x nguyên dương 
...................... 
Đọc kỹ để hiểu nội dung rõ bài toán: GT - KL 
Trả lời 
Chọn nghiệm thỏa mãn điều kiện của ẩn 
Đối chiếu nghiệm của phương trình vừa tìm được với điều kiện của ẩn ở trên 
Kết luận : Vậy ............. 
Biểu diễn các đại lượng chưa biết 
theo ẩn và các đại lượng đã biết 
Viết lại từng dữ kiện bài toán cho 
(nói lên mối liên hệ giữa các đại lượng) 
Biểu diễn đại lượng chưa biết theo ẩn 
Tìm các đại lượng của bài toán 
Biểu diễn đại lượng chưa biết 
theo các đại lượng khác 
Lập phương trình biểu thị mối 
quan hệ giữa các đại lượng 
Chú ý các dấu hiệu nói lên mối quan hệ giữa 
các đại lượng “bằng”, “lớn hơn”, “nhỏ hơn”, 
“có tổng bằng ...”, “hơn kém nhau....”, ..... 
Lập bảng biểu diễn các đại lượng 
trong bài toán theo ẩn đã chọn 
Đại số 8 - Chương 3: Phương trình bậc nhất một ẩn Giáo viên: Nguyễn Quốc Dũng 
SĐT: 0972299390 Cố Lên Nhé ! 2
VẤN ĐỀ I. Loại so sánh 
Trong đầu bài thường có các từ: 
 – nhiều hơn, thêm, đắt hơn, chậm hơn, ...: tương ứng với phép toán cộng. 
 – ít hơn, bớt, rẻ hơn, nhanh hơn, ...: tương ứng với phép toán trừ. 
 – gấp nhiều lần: tương ứng với phép toán nhân. 
 – kém nhiều lần: tương ứng với phép toán chia. 
Bài 1. Tìm hai số nguyên liên tiếp, biết rằng 2 lần số nhỏ cộng 3 lần số lớn bằng –87. 
ĐS: 18; 17  . 
Bài 2. Một phân số có tử số nhỏ hơn mẫu số là 8. Nếu thêm 2 đơn vị vào tử số và bớt mẫu số đi 3 
đơn vị thì ta được phân số bằng 
3
4
. Tìm phân số đã cho. 
 ĐS: 
7
15
Bài 3. Tổng của 4 số là 45. Nếu lấy số thứ nhất cộng thêm 2, số thứ hai trừ đi 2, số thứ ba nhân với 
2, số thứ tư chi cho 2 thì bốn kết quả đó bằng nhau. Tìm 4 số ban đầu. 
 ĐS: 8; 12; 5; 20. 
Bài 4. Thương của hai số là 3. Nếu tăng số bị chia lên 10 và giảm số chia đi một nửa thì hiệu của 
hai số mới là 30. Tìm hai số đó. 
 ĐS: 24; 8. 
Bài 5. Một đội công nhân sửa một đoạn đường trong 3 ngày. Ngày thứ nhất đội sửa được 
1
3
 đoạn 
đường, ngày thứ hai đội sửa được một đoạn đường bằng 
4
3
 đoạn được làm được trong ngày 
thứ nhất, ngày thứ ba đội sửa 80m còn lại. Tính chiều dài đoạn đường mà đội phải sửa. 
 ĐS: 360m. 
Bài 6. Hai phân xưởng có tổng cộng 220 công nhân. Sau khi chuyển 10 công nhân ở phân xưởng 1 
sang phân xưởng 2 thì 
2
3
 số công nhân phân xưởng 1 bằng 
4
5
 số công nhân phân xưởng 2. 
Tính số công nhân của mỗi phân xưởng lúc đầu. 
 ĐS: Phân xưởng 1 có 120 công nhân, phân xưởng 2 có 90 công nhân. 
Bài 7. Hai bể nước chứa 800 lít nước và 1300 lít nước. Người ta tháo ra cùng một lúc ở bể thứ nhất 
15 lít/phút, bể thứ hai 25 lít/phút. Hỏi sau bao lâu số nước ở bể thứ nhất bằng 
2
3
 số nước ở bể 
thứ hai? 
 ĐS: 40 phút. 
Bài 8. Trước đây 5 năm, tuổi Dung bằng nửa tuổi của Dung sau 4 năm nữa. Tính tuổi của Dung 
hiện nay. 
 ĐS: 14 tuổi. 
Bài 9. Tìm một số có chữ số hàng đơn vị là 2, biết rằng nếu xoá chữ số 2 đó thì số ấy giảm đi 200. 
 ĐS: 222. 
Bài 10. Gia đình Đào có 4 người: bố, mẹ, bé Mai và Đào. Tuổi trung bình của cả nhà là 23. Nếu 
viết thêm chữ số 0 vào bên phải tuổi bé Mai thì được tuổi của bố, tuổi của mẹ bằng 
9
10
 tuổi 
bố và gấp 3 lần tuổi của Đào. Tìm tuổi của mỗi người trong gia đình Đào. 
 ĐS: Tuổi của bố, mẹ, bé Mai và Đào lần lượt là: 40, 36, 4, 12. 
Bài 11. Nhân ngày 1 tháng 6, một phân đội thiếu niên được tặng một số kẹo. số kẹo này được chia 
hết và chia đều cho mọi đội viên trong phân đội. Để đảm bảo nguyên tắc chia ấy, đội trưởng 
đã đề xuất cách chia như sau: 
Đại số 8 - Chương 3: Phương trình bậc nhất một ẩn Giáo viên: Nguyễn Quốc Dũng 
SĐT: 0972299390 Cố Lên Nhé ! 
3
– Bạn thứ nhất nhận một viên kẹo và được lấy thêm 
1
11
 số kẹo còn lại. 
– Sau khi bạn thứ nhất lấy phần của mình, bạn thứ hai nhận 2 viên kẹo và được lấy thêm 
1
11
số kẹo còn lại. 
Cứ như thế đến bạn cuối cùng, thứ n, nhận n viên kẹo và được lấy thêm 
1
11
 số kẹo còn lại. 
Hỏi phân đội đó có bao nhiêu đội viên và mỗi đội viên nhận bao nhiêu viên kẹo. 
 ĐS: 10 đội viên, mỗi đội viện nhận 10 viên kẹo. 
Bài 12. Một người bán số sầu riêng thu hoạch được như sau: 
– Lần thứ nhất bán 9 trái và 
1
6
 số sầu riêng còn lại. 
– Lần thứ hai bán 18 trái và 
1
6
 số sầu riêng còn lại mới. 
– Lần thứ ba bá 27 trái và 
1
6
 số sầu riêng còn lại mới, v.v... 
Với cách đó thì bán lần sau cùng là vừa hết và số sầu riêng bán mỗi lần đều bằng nhau. 
Hỏi người đó đã bán bao nhiêu lần và số sầu riêng thu hoạch được là bao nhiêu trái? 
 ĐS: 225 trái, bán 5 lần. 
Bài 13. Ba lớp A, B, C góp sách tặng các bạn học sinh vùng khó khăn, tất cả được 358 cuốn. Tỉ số 
số cuốn sách của lớp A so với lớp B là 
6
11
. Tỉ số số cuốn sách của lớp A so với lớp C là 
7
10
. 
Hỏi mỗi lớp góp được bao nhiêu cuốn sách? 
 ĐS: Lớp A: 84 cuốn; lớp B: 154 cuốn; lớp C: 120 cuốn. 
Bài 14. Dân số tỉnh A hiện nay là 612060 người. Hàng năm dân số tỉnh này tăng 1%. Hỏi hai năm 
trước đây dân số của tỉnh A là bao nhiêu? 
 ĐS: 600000 người. 
Bài 15. Trong một trường học, vào đầu năm học số học sinh nam và nữ bằng nhau. Nhưng trong 
học kì 1, trường nhận thêm 15 học sinh nữ và 5 học sinh nam nên số học sinh nữ chiếm 51% 
số học sinh của trường. Hỏi cuối học kì 1, trường có bao nhiêu học sinh nam, học sinh nữ? 
 ĐS: 245 nam, 255 nữ. 
VẤN ĐỀ II. Loại tìm số gồm hai, ba chữ số 
  Số có hai chữ số có dạng: xy x y10  . Điều kiện: x y N x y, ,0 9,0 9     . 
  Số có ba chữ số có dạng: xyz x y z100 10   . Điều kiện: x y z N x y z, , ,0 9,0 , 9     . 
Bài 1. Tìm một số tự nhiên có hai chữ số, biết rằng: 
– Tổng hai chữ số là 12 
– Nếu đổi chỗ hai chữ số thì được một số mới lớn hơn số đó là 36. 
 ĐS: 48 
Bài 2. Tìm một số tự nhiên có hai chữ số, biết rằng: 
– Tổng hai chữ số là 10 
– Nếu viết số đó theo thứ tự ngược lại thì được một số mới nhỏ hơn số đó là 36. 
 ĐS: 73 
Bài 3. Một số tự nhiên có 5 chữ số. Nếu thêm chữ số 1 vào bên phải hay bên trái số đó ta được một 
số có 6 chữ số. Biết rằng nếu viết thêm vào bên phải số đó thì được một số lớn gấp ba lần số 
nhận được khi ta viết thêm vào bên trái số đó. Tìm số đó. 
 ĐS: 42857. 
Bài 4. Một số có hai chữ số, trong đó chữ số hàng chục gấp 3 lần chữ số hàng đơn vị. Nếu đổi chỗ 
Đại số 8 - Chương 3: Phương trình bậc nhất một ẩn Giáo viên: Nguyễn Quốc Dũng 
SĐT: 0972299390 Cố Lên Nhé ! 4
hai chữ số ta được một số có hai chữ số nhỏ hơn số ban đầu 18 đơn vị. Tìm số đó. 
 ĐS: 31. 
Bài 5. Một số tự nhiên có hai chữ số có tổng các chữ số bằng 7. Nếu thêm chữ số 0 vào giữa hai 
chữ số ta được một số có 3 chữ số lớn hơn số đã cho là 180. Tìm số đó. 
 ĐS: 25. 
VẤN ĐỀ III. Loại làm chung - làm riêng một việc 
  Khi công việc không được đo bằng số lượng cụ thể, ta coi toàn bộ công việc là một đơn vị 
công việc, biểu thị bởi số 1. 
  Năng suất làm việc là phần việc làm được trong một đơn vị thời gian. 
 Gọi A là khối lượng công việc, n là năng suất, t là thời gian làm việc. Ta có: A nt . 
  Tổng năng suất riêng bằng năng suất chung khi cùng làm. 
Bài 1. Hai người cùng làm một công việc trong 24 giờ thì xong. Năng suất của người thứ nhất bằng 
3
2
 năng suất của ngwòi thứ hai. Hỏi nếu mỗi người làm một mình cả công việc thì phải mất 
thời gian bao lâu? 
 ĐS: 40 giờ; 60 giờ. 
Bài 2. Một bồn chứa có đặt hai vòi nước chảy vào và một vòi tháo nước ra. 
– Bồn trống không, nếu mở riêng vòi thứ nhất thì sau 4 giờ bồn đầy nước. 
– Bồn trống không, nếu mở riêng vòi thứ hai thì sau 6 giờ bồn đầy nước. 
– Bồn trống không, nếu đồng thời mở cả ba vòi thì sau 7 giờ 12 phút bồn đầy nước. 
Hỏi nếu bồn chứa đầy nước, mở riêng vòi tháo nước thì sau bao lâu sẽ tháo hết nước ra? 
 ĐS: 3 giờ 36 phút. 
Bài 3. Một công nhân phải làm một số sản phẩm trong 18 ngày. Do đã vượt mức mỗi ngày 5 sản 
phẩm nên sau 16 ngày anh đã làm xong và làm thêm 20 sản phẩm nữa ngoài kế hoạch. Tính 
xem mỗi ngày anh đã làm được bao nhiêu sản phẩm. 
 ĐS: 75 sản phẩm. 
VẤN ĐỀ IV. Loại chuyển động đều 
  Gọi d là quãng đường động tử đi, v là vận tốc, t là thời gian đi, ta có: d vt . 
  Vận tốc xuôi dòng nước = Vận tốc lúc nước yên lặng + Vận tốc dòng nước 
  Vận tốc ngược dòng nước = Vận tốc lúc nước yên lặng – Vận tốc dòng nước 
Bài 1. Một xe vận tải đi từ địa điểm A đến địa điểm B với vận tốc 50 km/h, rồi từ B quay ngay về 
A với vận tốc 40 km/h. Cả đi và về mất một thời gian là 5 giờ 24 phút. Tìm chiều dài quãng 
đường từ A đến B. 
 ĐS: km120 . 
Bài 2. Một xe đạp khởi hành từ điểm A, chạy với vận tốc 20 km/h. Sau đó 3 giờ, một xe hơi đuổi 
theo với vận tốc 50 km/h. Hỏi xe hơi chạy trong bao lâu thì đuổi kịp xe đạp? 
 ĐS: 2 giờ. 
Bài 3. Một người đi xe gắn máy, đi từ địa điểm A đến địa điểm B trên một quãng đường dài km35 . 
Lúc trở về người đó đi theo con đường khác dài km42 với vận tốc kém hơn vận tốc lượt đi là 
6 km/h. Thời gian lượt về bằng 
3
2
 thời gian lượt đi. Tìm vận tốc lượt đi và lượt về. 
 ĐS: Vận tốc lượt đi là 30 km/h; vận tốc lượt về là 24 km/h. 
Bài 4. Một xe tải đi từ A đến B với vận tốc 50 km/h. Đi được 24 phút thì gặp đường xấu nên vận 
tốc trên quãng đường còn lại giảm còn 40 km/h. Vì vậy đã đến nơi chậm mất 18 phút. Tìm 
chiều dài quãng đường từ A đến B. 
 ĐS: km80 . 
Đại số 8 - Chương 3: Phương trình bậc nhất một ẩn Giáo viên: Nguyễn Quốc Dũng 
SĐT: 0972299390 Cố Lên Nhé ! 
5
Bài 5. Lúc 6 giờ 15 phút, một ô tô đi từ A để đên B với vận tốc 70 km/h. Khi đến B, ô tô nghỉ 1 giờ 
rưỡi, rồi quay về A với vận tốc 60 km/h và đến A lúc 11 giờ cùng ngày. Tính quãng đường 
AB. 
 ĐS: 105 km. 
Bài 6. Hàng ngày Tuấn đi xe đạp đến trường với vận tốc 12 km/h. Sáng nay do dậy muộn, Tuấn 
xuất phát chậm 2 phút. Tuấn nhẩm tính, để đến trường đúng giờ như hôm trước thì Tuấn phải 
đi với vận tốc 15 km/h. Tính quãng đường từ nhà Tuấn đến trường. 
 ĐS: 2 km. 
Bài 7. Một người đi xe máy từ thành phố Thanh Hoá và thành phố Vinh. Nếu chạy với vận tốc 25 
km/h thì sẽ muộn so với dự định là 2 giờ. Nếu chạy với vận tốc 30 km/h và giữa đường nghỉ 1 
giờ thì cũng muộn mất 2 giờ. Hỏi để đến nơi đúng giờ mà dọc đường không nghỉ thì xe phải 
chạy mỗi giờ bao nhiêu kilômet? 
 ĐS: 37,5 km. 
Bài 8. Hai ô tô khởi hành cùng một lúc để đi từ Huế và Đà Nẵng. Vận tốc xe thứ nhất là 40 km/h, 
vận tốc xe thứ hai là 60 km/h. Xe thứ hai đến Đà Nẵng nghỉ nửa giờ rồi quay lại Huế thì gặp 
xe thứ nhất ở cách Đà Nẵng 10 km. Tính quãng đường Huế - Đà Nẵng. 
 ĐS: 110 km. 
Bài 9. Quãng đường AD dài 9 km, gồm đoạn AB lên dốc, đoạn BC nằm ngang, đoạn CD xuống 
dốc. Một người đi bộ từ A đến D rồi quay trở về A hết tất cả 3 giờ 41 phút. Tính quãng đường 
BC, biết vận tốc lúc lên dốc của người đó là 4 km/h, lúc xuống dốc là 6 km/h và lúc đi trên 
đường nằm ngang là 5 km/h. 
 ĐS: 4 km. 
Bài 10. Một xe tải đi từ A đến B với vận tốc 45 km/h. Sau đó một thời gian, một xe con cũng xuất 
phát từ A với vận tốc 60 km/h và nếu không có gì thay đổi thì đuổi kịp xe tải tại B. Nhưng sau 
khi đi được nửa quãng đường AB thì xe con tăng vận tốc lên 75 km/h, nên sau đó 1 giờ thì 
đuổi kịp xe tải. Tính quãng đường AB. 
 ĐS: 450 km. 
Bài 11. Một đò máy xuôi dòng từ bến A đến bến B mất 4 giờ và ngược dòng từ B về A mất 5 giờ. 
Vận tốc của dòng nước là 2 km/h. Tìm chiều dài quãng đường từ A đến B. 
 ĐS: km80 . 
Bài 12. Một ca nô xuôi dòng từ A đến B mất 5 giờ và ngược dòng từ B đến A mất 6 giờ. Tính 
khoảng cách AB, biết vận tốc dòng nước là 2 km/h. 
 ĐS: 120 km. 
Bài 13. Hai bến sông A và B cách nhau 40 km. Cùng một lúc với ca nô xuôi dòng từ bến A, có một 
chiếc bè trôi từ bến A với vận tốc 3 km/h. Sau khi đến B, ca nô trở về bêbs A ngay và gặp bè 
khi bè đã trôi được 8 km. Tính vận tốc của ca nô. 
 ĐS: 27 km/h. 
Bài 14. Một chiếc thuyền đi từ bến A đến bến B hết 5 giờ, từ bến B đến bến A hết 7 giờ. Hỏi một 
đám béo trôi theo dòng sông từ A đến B hết bao lâu? 
 ĐS: 35 giờ. 
VẤN ĐỀ V. Loại có nội dung hình học 
  Hình chữ nhật có hai kích thước a, b. Diện tích: S ab ; Chu vi: P a b2( )  
  Tam giác vuông có hai cạnh góc vuông a, b. Diện tích: S ab1
2
 
Bài 1. Chu vi một khu vườn hình chữ nhật bằng m60 , hiệu độ dài của chiều dài và chiều rộng là 
m20 . Tìm độ dài các cạnh của hình chữ nhật. 
ĐS: m m5 ;25 . 
Bài 2. Một thửa đất hình chữ nhật có chu vi là m56 . Nếu giảm chiều rộng m2 và tăng chiều dài 
m4 thì diện tích tăng thêm m28 . Tìm chiều rộng và chiều dài thửa đất. 
Đại số 8 - Chương 3: Phương trình bậc nhất một ẩn Giáo viên: Nguyễn Quốc Dũng 
SĐT: 0972299390 Cố Lên Nhé ! 6
 ĐS: m m12 ;16 . 
Bài 3. Một khu vườn hình chữ nhật có chiều dài bằng 3 lần chiều rộng. Nếu tăng mỗi cạnh thêm 
m5 thì diện tích khu vườn tăng thêm m2385 . Tính độ dài các cạnh của khu vườn. 
 ĐS: m m18 ;54 . 
Bài 4. Hiệu số đo chu vi của hai hình vuông là m32 và hiệu số đo diện tích của chúng là m2464 . 
Tìm số đo các cạnh của mỗi hình vuông. 
 ĐS: cạnh hình vuông nhỏ là m25 ; cạnh hình vuông lớn là m33 . 
Bài 5. Một khu vườn hình chữ nhật có chu vi là m450 . Nếu giàm chiều dài đi 1
5
 chiều dài cũ và 
tăng chiều rộng thêm 
1
4
 chiều rộng cũ thì chu vi hình chữ nhật không đổi. Tính chiều dài và 
chiều rộng khu vườn. 
 ĐS: m m100 ;125 . 
Bài 6. Một khu đất hình chữ nhật có chiều dài hơn chiều rộng là 10m. Nếu chiều dài tăng thêm 6m, 
chiều rộng giảm đi 3m thì diện tích mới tăng hơn diện tích cũ là m212 . Tính các kích thước 
của khu đất. 
 ĐS: 20m, 30m.