Bài Tập Toán 11 HKI

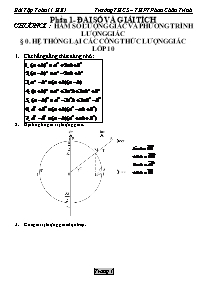
Phần 1- ĐẠI SỐ VÀ GIẢI TÍCH
CHƯƠNG I : HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
§ 0. HỆ THỐNG LẠI CÁC CÔNG THỨC LƯỢNG GIÁC LỚP 10
Các hằng đẳng thức đáng nhớ:
Định nghĩa giá trị lượng giác:
Các giá trị lượng giác đặc biệt:
Các công thức lượng giác cơ bản:
Công thức cộng: 
Công thức nhân đôi: 
Hệ quả: 
Công thức hạ bậc: 
Công thức nhân ba:
Công thức biến đổi tích thành tổng: 
Công thức biến đổi tổng thành tích: 
Cung liên kết: Sin – bù; cos – đối; phụ – chéo; hơn kém - tan, cot.
Hai cung bù nhau: và 
Hai cung đối nhau: và 
Hai cung phụ nhau: và 
Hai cung hơn kém : và 
Hai cung hơn kém : và 
“Sin góc lớn = cos góc nhỏ
 Cos góc lớn = trừ sin góc nhỏ”
Hệ quả:
§1. HÀM SỐ LƯỢNG GIÁC
A. KIẾN THỨC CƠ BẢN 
Hàm số
Tập xác định
Tập giá trị
Tính tuần hoàn
Tính chẵn lẻ
Chu kì 
Hàm số lẻ
Chu kì 
Hàm số chẵn
Chu kì 
Hàm số lẻ
Chu kì 
Hàm số lẻ
B. BÀI TẬP
Tìm tập xác định của các hàm số sau:
a)	b)	c)
d)	e)	f)
g)	h)	i)
j)	k)
Xét tính chẵn lẻ của các hàm số sau:
a)	b)	c)
d)	e)	f)
§2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
KIẾN THỨC CƠ BẢN 
Phương trình (1)
Phương pháp giải: Đưa phương trình (1) về dạng 
Nhận xét:
Phương trình có nghiệm khi và chỉ khi: 
Nếu dùng đơn vị radian: 
Tổng quát: 
Nếu a không phải là một trong các giá trị lượng giác đặc biệt, ta có:
Phương trình (2)
Phương pháp giải: Đưa phương trình (2) về dạng 
Nhận xét:
Phương trình có nghiệm khi và chỉ khi: 
Nếu dùng đơn vị radian: 
Tổng quát: 
Nếu a không phải là một trong các giá trị lượng giác đặc biệt, ta có:
Phương trình (3)
Phương pháp giải: Đưa phương trình (3) về dạng 
Nhận xét:
Phương trình có nghiệm với mọi giá trị a.
Nếu dùng đơn vị radian: 
Tổng quát: 
Nếu a không phải là một trong các giá trị lượng giác đặc biệt, ta có:
Phương trình (4)
Phương pháp giải: Đưa phương trình (4) về dạng 
Nhận xét:
Phương trình có nghiệm với mọi giá trị a.
Nếu dùng đơn vị radian: 
Tổng quát: 
Nếu a không phải là một trong các giá trị lượng giác đặc biệt, ta có:
F Lưu ý: 
Cách chuyển hàm: 
Cách loại dấu trừ:
Các trường hợp đặc biệt: 
BÀI TẬP
Giải các phương trình lượng giác sau:
a) 	b) 	
c) 	d) 	
e) 	f) 
g) 	h) 	
k) 	l)	
m)	n)
Giải các phương trình lượng giác sau: 
a)	b)
c)	d)	
e)	f)
g)	h)	
i)	j)	
k)	l)
m)	n)
Giải các phương trình lượng giác sau:
a) 	b) 	
c) 	d) 	
e) 	f) 
g)	h) 	
i) 
Giải các phương trình lượng giác sau:
a) 	b)	
c) 	d) 	
e) 	f)
g)
Giải các phương trình lượng sau:
a) 	b) 
c) 	d) 
e)	f) 
g)	h) 
i) 	j)
k)	l)	
m)	n)
o) 	p)
§3. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP
KIẾN THỨC CƠ BẢN 
I. Phương trình bậc hai theo một hàm số lượng giác:
Dạng:
F Đặt: Điều kiện 
Không có điều kiện t.
II. Phương trình thuần nhất bậc hai:
(*)
TH1: thế vào (*)
TH2: . Chia 2 vế (*) cho ta được phương trình bậc 2 theo 
Lưu ý: Phương trình với có thể đưa về dạng (*) như sau: 
III. Phương trình bậc nhất đối vối sinx và cosx : . 
Chia 2 vế của phương trình cho ta được: 
Vì nên tồn tại 1 cung sao cho .
Khi đó phương trình trở thành:
Điều kiện có nghiệm: 
Lưu ý: 
IV. Phương trình đối xứng và phản xứng : 
Đặt :
 Điều kiện 
 Điều kiện 
BÀI TẬP
Giải các phương trình lượng giác (phương trình bậc hai theo một hàm số lượng giác).
a)	b) 
c) 	d)	
e)	f)
g)	h) 
k) 	l)
m)	n)o)	p)
q)	r)	
s)	t)
u)	
Giải các phương trình lượng giác (phương trình bậc hai theo một hàm số lượng giác).
a) 	b) 
c) 	d) 
e) 	
f)
g) 	h)
i) 
Giải các phương trình lượng giác (phương trình thuần nhất bậc hai đối với và )
a) 
b)
c) 	
d) 
e) 	
f) 
g) 	
h) 
i) 	
k) 
l) 
m)
n)	
o)
p)	
q)
s)
t)
u)
Giải các phương trình lượng giác (phương trình bậc nhất đối với và ).
a) 	b) 	
c) 	d) 	
e)	f) 
g) 	h) 
k) 	l)	
m)	n)
o)	p)	
q)	r)	
s)	t)
u)	v) 
w)
Giải các phương trình lượng giác (phương trình đối xứng và phản xứng)
a) 
b) 
c)
b) 
c) 
d)
e)	
f)
g) 
h)
i)
j)
k) 
l)
m)
n)
o)
p) 
q)
r)
s)
t)
§4. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC KHÁC
Giải các phương trình sau:(đưa về phương trình tích)
a)sinx + sin3x + sin5x = 0
b)cos7x + sin8x = cos3x – sin2x
c)cos2x – cos8x + cos6x = 1
d)sin7x + cos22x = sin22x + sinx
Giải các phương trình sau:(dùng công thức hạ bậc đưa về phương trình tích)
	a)sin2x = sin23x	
b)sin2x + sin22x + sin23x = 
c)cos2x + cos22x + cos23x = 1	
d)cos2x + cos22x + cos23x + cos24x = 
Giải các phương trình sau: (đưa về phương trình tích)
a)1 + 2sinx.cosx = sinx + 2cosx
b)sinx(sinx – cosx) – 1 = 0
c)sin3x + cos3x = cos2x	
d)sin2x = 1 + cosx + cos2x
e)sinx(1 + cosx) = 1 + cosx + cos2x	
f)(2sinx – 1)(2cos2x + 2sinx + 1) = 3 – 4cos2x
g)(sinx – sin2x)(sinx + sin2x) = sin23x	
h)sinx + sin2x + sin3x = (cosx + cos2x + cos3x)
Giải các phương trình sau: (đưa về phương trình tích)
a)2cosx.cos2x = 1 + cos2x + cos3x	
b)2sinx.cos2x + 1 + 2cos2x + sinx = 0
c)3cosx + cos2x – cos3x + 1 = 2sinx.sin2x
d)cos5x.cosx = cos4x.cos2x + 3cos2x + 1
Giải các phương trình sau: 
	a)sin6x + cos6x = 	
b)sin8x + cos8x = 
c)cos4x + 2sin6x = cos2x	 
Giải các phương trình sau:
a)sin3x + cos3x + = cosx + sin3x
b)1 + sin2x + 2cos3x(sinx + cosx) = 2sinx + 2cos3x + cos2x
Giải các phương trình lượng giác sau:(Phương trình lượng giác có điều kiện)
Khi giải phương trình lượng giác ta phải đặt điều kiện nếu gặp một trong hai trường hợp sau:
Phương trình có chứa hàm số tang hoặc cotang (trừ phương trình bậc nhất và bậc hai theo 1 hàm số tang hoặc cotang)
Phương trình có chứa : Điều kiện
Phương trình có chứa : Điều kiện
Phương trình có chứa cả và : Điều kiện 
Phương trình có chứa ẩn ở mẫuĐiều kiện: mẫu 
a) 	b)c) 	d)
e)	f) 
g)	h)
i) 
j) sin4x + cos4x – cos2x + – 1 = 0
k)
l) 
m)
n)
PHƯƠNG TRÌNH LƯỢNG GIÁC TRONG CÁC ĐỀ THI ĐẠI HỌC
(ĐH 2002A) Tìm nghiệm thuộc khoảng của phương trình 
(ĐH 2002B) Giải phương trình 
(ĐH 2002D) Tìm x thuộc đoạn của phương trình
(ĐH 2003A) Giải phương trình
(ĐH 2003B) Giải phương trình
(ĐH 2003D) Giải phương trình 
(ĐH 2004B) Giải phương trình 
(ĐH 2004D) Giải phương trình
(ĐH 2005A) Giải phương trình 
(ĐH 2005B) Giải phương trình 
(ĐH 2005D) Giải phương trình
(ĐH 2006A) Giải phương trình
(ĐH 2006B) Giải phương trình 
(ĐH 2006D) Giải phương trình 
(ĐH 2007A) Giải phương trình
(ĐH 2007B) Giải phương trình 
(ĐH 2007D) Giải phương trình 
(ĐH 2008A) Giải phương trình 
(ĐH 2008B) Giải phương trình
(ĐH 2008D) Giải phương trình 
(CĐ 2008A) Giải phương trình 
(ĐH 2009A) Giải phương trình 
(ĐH 2009B) Giải phương trình
(ĐH 2009D) Giải phương trình 
(CĐ 2009A+B+D) Giải phương trình 
(ĐH 2010A) Giải phương trình 
(ĐH 2010B) Giải phương trình
(ĐH 2010D) Giải phương trình 
(CĐ 2010A+B+D) Giải phương trình 
(ĐH 2011A) Giải phương trình
(ĐH 2011B) Giải phương trình
(ĐH 2011D) Giải phương trình 
(CĐ 2011A+B+D) Giải phương trình 
(ĐH 2012A) Giải phương trình 
(ĐH 2012B) Giải phương trình
(ĐH 2012D) Giải phương trình
(CĐ 2012A+A1+B+D) Giải phương trình 
(ĐH 2013 A+A1) Giải phương trình 
(ĐH 2013B) Giải phương trình 
(ĐH 2013D) Giải phương trình 
(CĐ 2013A+A1+B+D) Giải phương trình 
(ĐH 2014 A+A1) Giải phương trình 
(ĐH 2014B) Giải phương trình 
CHƯƠNG II : TỔ HỢP – XÁC SUẤT
§1. QUY TẮC ĐẾM
LÝ THUYẾT:
I. Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai phương án A hoặc B. Nếu có m cách thực hiện phương án A, n cách thực hiện phương án B thì sẽ có m+n cách hoàn thành công việc.
II. Quy tắc nhân: Một công việc được thực hiện qua hai hành động liên tiếp A và B. Nếu có m cách thực hiện hành động A, m cách thực hiện hành động B thì sẽ có cách hoàn thành công việc.
Lưu ý: Đối với bài toán thành lập số ta phải xét hai trường hợp nếu thỏa mãn 3 điều kiện sau:
Đề cho có chữ số 0.
Số cần tìm có các chữ số khác nhau.
Số cần tìm là số chia hết cho 2 (số chẵn) hoặc số chia hết cho 5.
BÀI TẬP:
Trên giá sách có 10 quyển sách Toán, 8 quyển Vật lý và 6 quyển Hóa học. Hỏi có bao nhiêu cách chọn :
Một quyển sách bất kì.
Hai quyển sách khác môn
Ba quyển sách khác môn
Nam đến cửa hàng văn phòng phẩm để mua quà tặng bạn. Trong cửa hàng có ba mặt hàng : Bút, vở và thước trong đó có 5 loại bút, 4 loại vở và 3 loại thước. Hỏi Nam có bao nhiêu cách chọn một phần quà gồm một bút, một vở và một thước.
Lớp học có 20 học sinh nam và 15 học sinh nữ. Hỏi có bao nhiêu cách chọn một ban cán sự lớp gồm 4 bạn biết rằng mỗi học sinh làm không quá một nhiệm vụ trong ban cán sự: 
Một lớp trưởng, một lớp phó học tập, một lớp phó lao động, một lớp phó văn thể mỹ. 
Một lớp trưởng, một lớp phó học tập, một lớp phó lao động, một lớp phó văn thể mỹ thỏa lớp trưởng phải là học sinh nam và lớp phó văn thể mỹ phải là học sinh nữ.
Có 10 cặp vợ chồng đi dự tiệc. Tính số cách chọn một người đàn ông và một người phụ nữ trong bữa tiệc để phát biểu ý kiến, sao cho:
Hai người đó là vợ chồng	
Hai người đó không là vợ chồng
Giữa hai thành phố A và B có 5 con đường đi. Hỏi có bao nhiêu cách đi từ A đến B rồi trở về A mà không có con đường nào được đi 2 lần?
Chợ Bến Thành có 4 cồng ra vào. Hỏi một người đi chợ:
Có mấy cách ra vào chợ.
Có mấy cách ra vào chợ bằng hai cổng khác nhau?
Từ các chữ số 1, 2, 3, 4, 5, 6, có thể lập được bao nhiêu số tự nhiên:
Có ba chữ số.
Có ba chữ số khác nhau.
Lẻ và có ba chữ số.
Chẵn và có ba chữ số.	
Lẻ và có ba chữ số khác nhau.
Chẵn và có ba chữ số khác nhau.
Từ các chữ số 0, 1, 2, , 8, 9 có thể lập được bao nhiêu số tự nhiên:
Có bốn chữ số	
Có bốn chữ số khác nhau.
Lẻ và có bốn chữ số. 
Chẵn và có bốn chữ số.
Lẻ và có 4 chữ số khác nhau.
Có bốn chữ số và chia hết cho 5.	
(*)Chẵn và có 4 chữ số khác nhau.
(*)Có bốn chữ số khác nhau và chia hết cho 5.
§2. HOÁN VỊ – CHỈNH HỢP – TỔ HỢP
LÝ THUYẾT:
I. Hoán vị: Từ n phần tử sắp thứ tự
1)Định nghĩa: Cho tập hợp A gồm n phần tử (). Mỗi cách sắp thứ tự n phần tử của tập A được gọi là một hoán vị của n phần tử đó.
2)Số hoán vị của n phần tử: 
n!: đọc là “n giai thừa”
II. Tổ hợp: Từ n lấy k
1)Định nghĩa: Cho tập hợp A gồm n phần tử (). Lấy ra k phần tử, mỗi kết quả thu được được gọi là một tổ hợp chập k của n phần tử.
2)Số tổ hợp chập k của n phần tử: 
III. Chỉnh hợp: Từ n lấy k sắp thứ tự
1)Định nghĩa: Cho tập hợp A gồm n phần tử (). Lấy ra k phần tử và sắp xếp chúng theo một thứ tự nào đó, mỗi kết quả thu được được gọi là một chỉnh hợp chập k của n phần tử.
2)Số chỉnh hợp chập k của n phần tử: 
B. BÀI TẬP:
Từ các chữ số 1,2,3,4,5,6,7,8,9 có thể thành lập được bao nhiêu số nguyên dương trong mỗi trường hợp sau:
Có 5 chữ số đôi một khác nhau.
Số chẵn có 5 chữ số đôi một khác nhau khác nhau.
Số lẻ có 5 chữ số đôi một khác nhau khác nhau.
Từ các chữ số 0, 1, 2, 3, 4, 5 ,6,7,8 có thể lập được bao nhiêu số tự nhiên:
Có 4 chữ số khác nhau và là số lẻ.
Có 4 chữ số khác nhau và chia hết cho 5.
Có 4 chữ số sao cho chữ số hàng nghìn và chữ số hàng đơn vị giống nhau.
Cho các chữ số 1, 2, 3, 4, 5, 6.
Có thể lập được bao nhiêu số tự nhiên có sáu chữ số khác từ các chữ số trên?
Tính tổng tất cả các số lập được ở câu a)?
Cho các chữ số: 0, 1, 2, 3, 4, 5, 6, 7. Hỏi có thể lập được bao nhiêu số tự nhiên có bốn chữ số khác nhau sao cho:
Số đó chia hết cho 10.
Số đó phải có mặt chữ số 2.
Có bao nhiêu cách xếp 5 bạn nam và 5 bạn nữ vào 10 ghế được sắp thành hàng ngang, sao cho:
Nam và nữ ngồi xen kẽ nhau
Các bạn nam ngồi cạnh nhau.
Có bao nhiêu cách xếp chỗ ngồi cho 10 bạn, trong đó có An và Bình, vào 10 ghế xếp thành hàng ngang, sao cho:
Hai bạn An và Bình ngồi cạnh nhau	
Hai bạn An và Bình không ngồi cạnh nhau.
Một kệ sách có 5 quyển sách Toán, 4 quyển sách Lý, 3 quyển sách Văn. Các quyển sách đều khác nhau. Hỏi có bao nhiêu cách sắp xếp các quyển sách trên:
Một cách tuỳ ý
Theo từng môn
Theo từng môn và sách tóan nằm ở giữa.
Có bao nhiêu cách sắp xếp 5 bạn học sinh A,B,C,D,E ngồi vào một chiếc ghế dài sao cho:
Bạn C ngồi chính giữa
Hai bạn A và E ngồi ở hai đầu ghế.
Có 4 tem thư khác nhau và 4 bì thư khác nhau. Hỏi có bao nhiêu cách dán tem vào bì thư?
Lớp học có 20 học sinh nam và 15 học sinh nữ. Hỏi có bao nhiêu cách chọn một nhóm 5 học sinh trong lớp để đi thăm bà mẹ Việt Nam anh hùng sao cho:
Tất cả là học sinh nam.	
Gồm 3 nam và 2 nữ
Cô giáo chia 4 quả táo, 3 quả cam và 2 quả chuối cho 9 em học sinh. Hỏi có bao nhiêu cách chia khác nhau ?
Một lớp có 40 học sinh, trong đó gồm 25 nam và 15 nữ. Giáo viên chủ nhiệm muốn chọn một ban cán sự lớp gồm 4 em. Hỏi có bao nhiêu cách chọn, nếu:
4 học sinh được chọn tuỳ ý.
Có 2 nam và 2 nữ
Có ít nhất 1 nam và 1 nữ
Có ít nhất 1 nam.
Một túi đựng 6 viên bi trắng và 5 viên bi xanh. Lấy ra 4 viên bi từ túi đó, hỏi có bao nhiêu cách lấy được:
4 viên bi cùng màu?
2 viên bi trắng và 2 viên bi xanh?
Một đa giác lồi 20 cạnh, hỏi có tất cả bao nhiêu đường chéo ?
Từ 24 học sinh giỏi Toán gồm 16 nam, 8 nữ, người ta muốn thành lập một đội tuyển gồm 7 người. Hỏi có bao nhiêu cách thành lập nếu:
Đội tuyển có nhiều nhất 2 nữ.
Đội tuyển có ít nhất 3 nam
Nam sinh A và nữ sinh B phải cùng được hoặc cùng không được vào đội tuyển
Nam sinh X và nữ sinh Y không thể cùng được chọn vào đổi tuyển.
Có 8 quả cầu xanh, 4 quả cầu vàng, 6 quả cầu đỏ (các quả cầu đôi một khác nhau). Có bao nhiêu cách lấy ra 6 quả cầu trong mỗi trường hợp sau đây:
6 quà được lấy tùy ý.
Phải có 2 cầu xanh, 2 cầu vàng, 2 cầu đỏ.
Phải có đúng 2 quả cầu đỏ.
Phải có ít nhất 2 quả cầu đỏ.
Phải có đủ 3 màu.	
Có bao nhiêu cách chia 20 người thành 3 nhóm: nhóm 1 có 10 người, nhóm 2 có 7 người và nhóm 3 có 3 người.
Một tổ có 9 học sinh gồm 5 nam(trong đó có Trung) và 4 nữ(trong đó có Lan)
Có bao nhiêu cách xếp 9 học sinh đó vào một dãy bàn có 9 ghế sao cho các học sinh nữ luôn ngồi gần nhau?
Chọn ra 2 học sinh để thi văn nghệ chào mừng ngày Nhà Giáo Việt Nam. Hỏi có bao nhiêu cách nếu
Trong 2 học sinh được chọn có 1 nam và 1 nữ.
Một trong 2 học sinh được chọn phải có Lan hoặc Trung.
Nếu chia 9 học sinh trên thành 3 nhóm học tập bằng nhau về số lương, hỏi có mấy cách chia?
§3. NHỊ THỨC NIU – TƠN
KIẾN THỨC CƠ BẢN
I. Các công thức lũy thừa:
II. Công thức nhị thức Niu – tơn:
 III. Số hạng tổng quát: hoặc 
Chú ý: Trong khai triển: có 3 số hạng
Số hạng chứa là: 
Số hạng chứa là: 
Số hạng không chứa (chứa ) là: 9
Hệ số của là: 1
Hệ số của là: 
BÀI TẬP:
Khai triển các nhị thức sau:
a) 	b) 
c) 	d)
Khai triển nhị thức sau theo lũy thừa tăng dần của :
a) 	b) 
c) 	d)
Tìm hệ số của trong khai triển của biểu thức
Tìm hệ số của trong khai triển của biểu thức 
Tìm hệ số của trong khai triển của biểu thức 
Tìm số hạng không chứa trong khai triển 
Tìm số hạng không chứa trong khai triển 
Tìm số hạng không chứa trong khai triển 
Tìm số hạng không chứa trong khai triển 
Tìm số hạng không chứa trong khai triển 
Tìm hệ số của trong khai triển của biểu thức 
Tìm số hạng chính giữa trong các khai triển sau: 
a) 	b)
c)	d)
(*) Biết hệ số của trong khai triển của là 90. Tìm giá trị n?
§4. PHÉP THỬ VÀ BIẾN CỐ
KIẾN THỨC CƠ BẢN:
I. Phép thử ngẫu nhiên (gọi tắt là phép thử) là một thí nghiệm, một phép đo hay một sự quan sát hiện tương nào đó mà:
- Kết quả của nó không đoán trước được.
- Có thể xác định được tập hợp tất cả các kết quả có thể xảy ra của phép thử đó.
II. Không gian mẫu: Tập hợp tất cả các kết quả có thể xảy ra của một phép thử. Kí hiệu (ô-mê-ga).
III. Biến cố: Là một tập con của không gian mẫu.
- Biến cố không là biến cố không bao giờ xảy ra.
- Biến cố chắc chắn là biến cố luôn xảy ra
IV. Phép toán trên các biến cố:
- : Hợp của các biến cố A và B ( xảy ra A xảy ra hoặc B xảy ra).
- (hay ): Giao của các biến cố A và B ( xảy ra A và B đồng thời xảy ra).
 thì ta nói A và B là 2 biến cố xung khắc (không đồng thời xảy ra).
- được gọi là biến cố đối của biến cố A. (A và xung khắc và )
BÀI TẬP: 
Gieo một con súc sắc cân đối, đồng chất và quan sát số chấm xuất hiện.
Mô tả không gian mẫu.
Xác định các biến cố sau: A: ‘‘Xuất hiện mặt chẵn chấm’’ ; B: ‘‘Xuất hiện mặt lẻ chấm’’ ; C: ‘‘Xuất hiện mặt có số chấm không nhỏ hơn ba’’.
Trong các biến cố trên, tìm các cặp biến cố xung khắc.
Trong hộp có 3 bi trắng và 4 bi đỏ. Lấy ngẫu nhiên đồng thời 2 bi trong hộp.
Xác định không gian mẫu.
Xác định các biến cố: A: ‘‘Hai bi cùng màu đỏ’’ ; B: ‘‘Hai bi cùng màu trắng’’ ; C: ‘‘Hai bi cùng màu’’ ; D: ‘‘Hai bi khác màu’’.
Trong các biến cố trên, tìm biến cố xung khắc, biến cố đối nhau.
Gieo một đồng tiền, sau đó gieo một con súc sắc và quan sát sự xuất hiện mặt sấp (S) và mặt ngửa (N) của đồng tiền và số chấm trên mặt con súc sắc.
Xây dựng không gian mẫu.
Xác định các biến cố sau:
A: ‘‘Đồng tiền xuất hiện mặt sấp và con súc sắc xuất hiện mặt chẵn chấm’’
B: ‘‘Đồng tiền xuất hiện mặt ngửa và con súc sắc xuất hiện mặt lẻ chấm’’
C: ‘‘Mặt lẻ chấm xuất hiện’’
§5. XÁC SUẤT CỦA CÁC BIẾN CỐ
KIẾN THỨC CƠ BẢN:
I. Định nghĩa: Xác suất của biến cố A là 1 số thực nằm trên đoạn được xác định bằng công thức 
Trong đó:
: Số kết quả thuận lợi cho biến cố A.
: Số phần tử của không gian mẫu.
II. Tính chất: 
, với mọi biến cố A.
Nếu A và B xung khắc thì: (công thức cộng xác suất)
, với mọi biến cố A.
BÀI TẬP:
Lấy ngẫu nhiên một thẻ từ một hộp chứa 20 thẻ được đánh số từ 1 đến 20. Tìm xác suất để thẻ được lấy ghi số:
Chẵn
Chia hết cho 3
Lẻ và chia hết cho 3
Gọi E là tập hợp các số gồm 2 chữ số khác nhau được lập thành từ các số 1, 2, 3, 4, 5, 6. Lấy ngẫu nhiên một phần tử của E.
Tính xác suất để được số chẵn.
(*) Tính xác suất để được số chia hết cho 9.
Một hộp có các thẻ được đánh số 1, 2, 3, 4, 5, 6. Rút ngẫu nhiên 4 thẻ và sắp theo thứ tự từ trái qua phải ta được số tự nhiên có 4 chữ số. Tính xác suất sao cho:
Số tạo thành là số chẵn.
Số tạo thành là số lẻ.
Số tạo thành là số chia hết cho 5.
Gieo một đồng tiền 3 lần và quan sát sự xuất hiện mặt sấp (S), mặt ngửa (N).
Xây dựng không gian mẫu.
Tính xác suất của các biến cố:
A: “Lần gieo đầu xuất hiện mặt sấp”
B: “Ba lần xuất hiện các mặt như nhau”
C: “Đúng hai lần xuất hiện mặt sấp”
D: “Ít nhất một lần xuất hiện mặt sấp”
Gieo một con súc sắc cân đối đồng chất 2 lần.
Mô tả không gian mẫu.
Xác định và tính xác suất các biến cố sau:
A: “Số chấm ở hai lần gieo như nhau”
B: “Tổng số chấm không nhỏ hơn 10”
C: “Mặt 5 chấm xuất hiện trong lần gieo đầu”
D: “Mặt 5 chấm xuất hiện ít nhất một lần”
E: “Tổng số chấm là 8”
F: “Tổng số chấm là lẻ hoặc chia hết cho 3”
G: “Số chấm xuất hiện trên 2 lần gieo không giống nhau”
Gieo một đồng tiền, sau đó gieo một con súc sắc.
Mô tả không gian mẫu.
Tính xác suất của các biến cố sau:
A: “Đồng tiền xuất hiện mặt sấp và con súc sắc xuất hiện mặt chẵn chấm”
B: “Đồng tiền xuất hiện mặt ngửa và con súc sắc xuất hiện mặt lẻ chấm”
C: “Mặt 6 chấm xuất hiện”
Có 9 miếng bìa như nhau được ghi từ 1 đến 9. Lấy ngẫu nhiên hai miếng bìa và xếp theo thứ tự từ trái sang phải. Tính xác suất của các biến cố sau:
A: “Số tạo thành là số chẵn”
B: “Số tạo thành là số chia hết cho 5”
C: “Số tạo thành có chữ số hàng chục nhỏ hơn chữ số hàng đơn vị”
Một bình đựng 8 viên bi xanh và 4 viên bi đỏ, các viên bi đôi một khác nhau. Lấy ngẫu nhiên 3 viên bi. Tính xác suất để được:
3 viên bi xanh.
3 viên bi đỏ.
3 viên bi cùng màu.
Ít nhất hai viên bi xanh.
Trong một hộp có 20 quả cầu khác nhau gồm 12 quả trắng và 8 quả đen.
Tính xác suất để khi lấy bất kỳ 3 quả có đúng 1 quả màu đen.
Tính xác suất để khi lấy bất kỳ 4 quả có ít nhất 1 quả màu đen.
Một bình đựng 5 viên bi xanh, 3 viên bi vàng, 4 viên bi đỏ. Lấy nhẫu nhiên 3 viên bi. Tính xác suất các biến cố sau:
A: “Lấy được 3 viên bi xanh”
B: “Lấy được ít nhất 1 bi vàng”
C: “Lấy được 3 viên bi cùng màu”
Một hộp bóng đèn có 12 bóng, trong đó có 7 bóng tốt. Lấy ngẫu nhiên 3 bóng. Tính xác suất để lấy được:
Ba bóng tốt.
Ít nhất 2 bóng tốt.
Ít nhất 1 bóng tốt.
(*) Cho 8 quả cân có khối lượng lần lượt là 1kg, 2kg, 3kg, 4kg, 5kg, 6kg, 7kg, 8kg. Chọn ngẫu nhiên 3 quả cân trong số đó.
Có bao nhiêu cách chọn như thế?
Tính xác suất để tổng khối lượng 3 quả cân được chọn không vượt quá 9 kg.
Có hai bình chứa các viên bi khác nhau. Bình thứ nhất có 3 viên bi xanh, 2 viên bi vàng, 1 viên bi đỏ. Bình thứ hai có 2 viên bi xanh, 1 viên bi vàng, 3 v