Bài tập ôn học kì 1 Hình 9

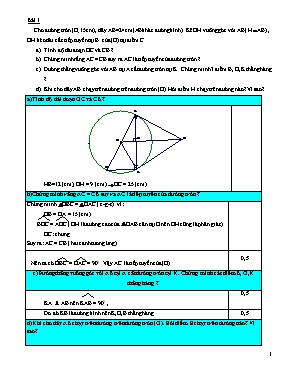
Bài 1
 Cho đường tròn (O;15cm) , dây AB=24cm(AB khác đường kính) .Kẽ OH vuông góc với AB( HAB) , OH kéo dài cắt tiếp tuyến tại B của (O) tại điểm C . 
Tính độ dài đoạn OC và CB ?
Chứng minh rằng AC = CB suy ra AC là tiếp tuyến của đường tròn ?
Đường thẳng vuông góc với AB tại A cắt đường tròn tại K. Chứng minh 3 điểm B, O,K thẳng hàng ?
Khi cho dây AB chạy trên đường trên đường tròn (O). Hỏi điểm H chạy trên đường nào? Vì sao?
a)Tính độ dài đoạn OC và CB ?
HB=12 (cm); OH = 9 (cm) OC = 25 (cm)
b)Chứng minh rằng AC = CB suy ra AC là tiếp tuyến của đường tròn ?
Chứng minh OBC =OAC ( c-g-c) vì:
OB = OA = 15 (cm)
 BOC = AOC ( OH là đường cao của OAB cân tại O nên OH cũng là phân giác)
OC: chung
Suy ra: AC = CB ( hai canh tương ứng)
 Nên ta có OBC = OAC = 900 . Vậy AC là tiếp tuyến của (O)
0,5
c)Đường thẳng vuông góc với AB tại A cắt đường tròn tại K. Chứng minh các điểm B, O,K thẳng hàng ?
KA AB nên KAB = 900 , 
0,5
Do đó KB là đường kính nên K,O,B thẳng hàng
0,5
d)Khi cho dây AB chạy trên đường trên đường tròn (O). Hỏi điểm H chạy trên đường nào? Vì sao?
Khi dây AB = 24cm chạy trên đường tròn tâm (O) bán kính 15cm thì OH = 9cm. Do đó H cách O một khoảng 9 cm nên H chạy trên đường tròn (O;9cm)
0,5
Bài 2:
	Cho đường tròn tâm O bán kính 3cm. Từ một điểm A cách O là 5cm vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm).
	a) Chứng minh AO vuông góc với BC;
	b) Kẻ đường kính BD. Chứng minh rằng DC song song với OA;
	c) Tính chu vi và diện tích tam giác ABC.
	d) Qua O kẻ đường thẳng vuông góc với BD, đường thẳng này cắt tia DC tại E. Đường thẳng AE và OC cắt nhau ở I; đường thẳng OE và AC cắt nhau ở G.
 Chứng minh IG là trung trực của đoạn thẳng OA. 
B
D
C
I
E
G
A
O
H
Ta có OB = OC = R = 2(cm)
 AB = AC ( Tính chất của hai tiếp tuyến cắt nhau)
=> AO là đường trung trực của BC hay OA BC
Xét tam giác BDC có OB = OD = OD = BD (= R)
=> Tam giác BDC vuông tại C => DC BC tại C
 Vậy DC // OA ( Vì cùng vuông góc với BC)
- Xét tam giác ABO vuông có BO AB ( theo tính chất tiếp tuyến)
=> AB = 
Gọi H là giao điểm của AO và BC
Vì AO là trung trực của BC nên HB = HC = 
Tam giác ABO vuông tại B có đường cao BH
=> HB.OA = OB.AB ( Hệ thức lượng trong tam giác vuông)
Tính được HB = 2,4 cm; BC = 4,8 cm
Lại có AB2 = OA.AH => AH = 3,2cm
Vậy chu vi tam giác ABC là AB + AC + BC = 
 = 4 + 4 + 4,8 =12,8 (cm)
Diện tích tam giác ABC là: 
Chứng minh được hai tam giác ABO và tam giác EOD bằng nhau (g.c.g)
Chứng minh được Tứ giác ABOE là hình chữ nhật => OE AI
Chứng minh được tam giác AOI cân ở I
Sử dụng tính chất 3 đường cao của tam giác chỉ ra được IG là đường cao đồng thời là trung trực của đoạn thẳng OA.
Bài 3:
Cho ( O,R ), lấy điểm A cách O một khoảng bằng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K. 
 a) Chứng minh: Tam giác OAK cân tại K.
 b) Đường thẳng KI cắt AB tại M. Chứng minh: KM là tiếp tuyến của đường tròn (O).
 c) Tính chu vi tam giác AMK theo R. 
a) 
Ta có: AB OB ( T/c tiếp tuyến ) 
 OK OB ( gt ) 
Mà (T/c hai tiếp tuyến cắt nhau)
Vậy OKA cân tại K.
b) Ta có : OI = R , OA = 2R => IA = R 
 => KI là trung tuyến OKA
 Mà OKA cân tại K ( Cmt)
 => KI OA Hay KM OA
 Vậy KM là tiếp tuyến (O) 
c) Xét AOB (), có: OA = 2R , OB = R => AB =
= AM + MK + AK = AM + MI + IK + KA
Mà MB = MI 
 KI = KC (t/c hai tiếp tuyến cắt nhau) 
 AB = AC
=>= AM+MB+KC+KA = AB+AC = 2AB = 2
Bài 4:
Cho đường tròn tâm (O; R) và một điểm A có AO = 2R . Kẻ tiếp tuyến AB, AC và cát tuyến AMN với đường tròn. Gọi I là trung điểm của MN . BC cắt OA và MN tại H và K .
1. Chứng minh : AO BC .
2. Tính độ dài OH theo R. 	
3 Chứng minh tam giác ABC là tam giác đều 	
4. Chứng minh AI. AK = AO. AH 
Hình vẽ 
AB = AC ( Tính chất hai tiếp tuyến cắt nhau )
OB= OC =R
Suy ra AO là đường trung trực của đoạn BC 
suy ra AOBC 
 Chỉ ra OAB vuông tại B, AOBC tại H 
OB2 = OA.OH ==> OH = = 
Sin BAO = 
BAC =2 .BAO = 600 (1)
ABC có AB = AC suy ra ABC cân tại A (2)
 Từ (1) và(2) Suy ra ABC là tam giác đều 
IN = IM (GT) Suy ra OI MN hay OIA = 900 
AIO và AHK có 
OIA = 900 và AHK= 900 
IAO chung 
Suy ra AIO AHK(g.g)
Suy ra : => AI.AK = AO.AH 
Bài 5: Cho nửa đường tròn tâm 0 đường kính AB =2R. Trên nửa mặt phẳng chứa nửa đường tròn này dựng các tia Ax, By cùng vuông góc với AB. Qua điểm M thuộc nửa đường tròn (M khác A và B) kẻ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C và D.
a) Chứng minh .
b) Chứng minh tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.
c) AD cắt BC tại I, MI cắt AB tại H. Chứng minh MH ^ AB.
d) Biết AM = R. Tính diện tích tam giác BMD theo R.
a) Theo tính chất hai tiếp tuyến cắt nhau, ta có:
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có:
	AC = CM; BD = DM
=> AC.BD = CM.DM = R2 (không đổi)
c) Ta có DAIC ~ DDIB => 
=> => IM // AC
Mà AC ^ AB nên IM ^ AB
Hay HM ^ AB.
d) (áp dụng Pytago và DAMB)
- Chứng minh DBMD đều
(đvdt) 
Bài 6: Cho tam giác ABC cân tại A. Gọi M là trung điểm CB.
Chứng minh M thuộc đường tròn tâm O đường kính AB
Kẻ OH vuông góc MB tại H, OH cắt tiếp tuyến (O) tại B ở I. Chứng minh: IM là tiếp tuyến (O).
Cho AB = 20cm, AM = 12cm. Tính OI và BI.
Gọi K là giao điểm OI và (O). Chứng minh BK là phân giác của góc MBI.
a
Ta có: ABC cân tại A, mà M là trung điểm BC => 
 => M thuộc đường tròn tâm (O) đường kính AB.
b
Xét OBI và OMI có:
OM = OB, OI là cạnh chung, ( OH là đường cao của tam giác MOB cân tại O nên cũng là phân giác )
Suy ra: OBI = OMI (c-g-c) 
Do đó 
Vậy IM là tiếp tuyến (O) tại M.
c
Xét OBI vuông tại B, BH OI
Suy ra: OB2 = OH.OI
=> OI= OB2 : OH = 102: 6 = (cm), ( OH = ½ AM)
=> BI2 = OI2 – OB2 = =>BI = (cm) 
d
Ta có BHK vuông tại H => 
OBI vuông tại B => 
Mà (OKB cân tại O)
Do đó: 
 Bài 7: Cho tam giác ABC cân tại A () có các đường cao AD, BE cắt nhau tại H. Gọi O là trung điểm của AH.
Chứng minh 3 điểm A, H, E cùng thuộc đường tròn ( O).
Chứng minh DE là tiếp tuyến của (O).
Biết DH = 2cm, AH = 6cm. Hãy tính số đo góc ADE.(Làm tròn độ).
a. Vì O là trung điểm của AH OA = OH =AH 
Tam giác AEH vuông tại E có EO là đường trung tuyến OE =AH 
OA = OH = OE 3 điểm A, H, E cùng thuộc (O).
b.Vì OA = OE Tam giác ABC cân tại A (1)
Tam giác ABC cân tại A có AD là đường cao nên cũng là đương trung tuyến D là trung điểm của BC.DB = DC =BC
Tam giác BEC vuông tại E có ED là đường trung tuyếnDE =BC
DB = DE DBE cân tại D = (2)
Ta lại có: (cùng phụ ) (3)
Từ (1), (2), (3) 
Mà OE ED tại E.
Vậy DE là tiếp tuyến của (O) tại E. 
c. Ta có AH = 6cm OH = OE = 3cm; DH = 2cm.OD = 5cm.
Trong tam giác vuông OED có: SinODE = = 0,6
 hay . 
Bài 8:
Cho DABC vuông tại A, có AB = 3cm, BC = 6cm.
Tính độ dài cạnh AC, số đo góc B và góc C.
Vẽ (O) ngoại tiếp DABC. Đường cao AH của DABC cắt (O) tại D. Chứng minh BC là đường trung trực của AD.
Tiếp tuyến tại D của (O) cắt đường thẳng BC tại E. Chứng minh EA là tiếp tuyến của (O).
Chứng minh EA2 = EB. EC
a) Tính độ dài cạnh AC, số đo góc B và góc C.
D vuông ABC, có:
 *) AC =cm
*) cos B = AB : BC = 0,5 Þ = 60o
Þ = 90o - 60o = 30o
b) Chứng minh BC là đường trung trực của AD.
Tâm đường tròn ngoại tiếp DABC là trung điểm BC
Xét (O), ta có:
BC ^ AD tại H ( gt) (1)
Þ H là trung điểm của dây AD (2)
Từ (1) và (2) suy ra: BC là đường trung trực của AD.
 c) Chứng minh EA là tiếp tuyến của (O).
Dcân ABO ( OA = OB), có:
OH là đường trung trực ( cmt)
Þ OH là đường phân giác Þ Ô1 = Ô2
Xét DAEO và DDEO, ta có:
OA = OD = R; Ô1 = Ô2 ( cmt) ; EO: chung
Suy ra :DAEO = DDEO ( c.g.c)
 Þ EA ^ OA tại A
Þ EA là tiếp tuyến của (O)
d) Chứng minh EA2 = EB. EC
Ta có : OA = OB = AB = 3cm
Nên DOAB là tam giác đều
Þ
Þ Â1 = EÂO – BÂO = 90o – 60o = 30o
Xét D EAB và D ECA, ta có :
Ê1 : chung; Â1 = = 30o
 Suy ra : D EAB D ECA(g.g)
Bài 9: Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn (O) sao cho 
OA = 2R. Từ A vẽ tiếp tuyến AB của đường tròn (O) (B là tiếp điểm).
 1) Chứng minh tam giác ABO vuông tại B và tính độ dài AB theo R 
 2) Từ B vẽ dây cung BC của (O) vuông góc với cạnh OA tại H. Chứng minh AC là tiếp tuyến của đường tròn (O). 
 3) Chứng minh tam giác ABC đều. 
 4) Từ H vẽ đường thẳng vuông góc với AB tại D. Đường tròn đường kính AC cắt cạnh DC tại E. Gọi F là trung điểm của cạnh OB. Chứng minh ba điểm A, E, F thẳng hàng. 
1) Ta có: (AB là tiếp tuyến của(O) tại B)
 Þ DABO vuông tại B 
 Þ (Đ/L Pytago)
 Þ 
 Þ 
2) Ta có DBOC cân tại O (OB = OC = R)
 Mà OH là đường cao ( BC ^ OA tại H)
 Þ OH là đường phân giác của DBOC
 Þ 
 Chứng minh DAOC = DAOB (c-g-c)
 Þ 
 Mà (AB là tiếp tuyến của(O) tại B)
 Þ Þ AC ^ OC mà C thuộc (O)
 Þ AC là tiếp tuyến của đường tròn (O) 
3) Chứng minh DABC cân tại A (1)
Xét DABO vuông tại 0, có 
 Þ 
 Ta có: AO là tia phân giác của góc BAC (T/c 2 tiếp tuyến cắt nhau) Þ (2)
 Từ (1) và (2) suy ra DABC đều 
Gọi I là giao điểm của AF và HD
Áp dụng hệ quả Talet để I là trung điểm HD
Gọi K là trung điểm BD
 Chứng minh KI là đường trung bình của DBHD
Þ KI // HB Mà HB ^ OA tại H (gt)
Þ KI ^ AH 
 Chứng minh I là trực tâm của DAHK
Þ AI là đường cao của DAHK Þ AF ^ HK (3)
Chứng minh HK là đường trung bình của DBDCÞ HK // CD (4) 
Từ (3) và (4) Þ AF ^ CD 
 Ta có: DAEC nội tiếp đường tròn đường kính AC
 Þ DAEC vuông tại E Þ AE ^ CD mà AF ^ CD (cmt)
Vậy Ba điểm A, E, F thẳng hàng 
Bài 10:
Cho góc xOy bằng 1200, đường tròn (O) cắt tia Ox, tia Oy lần lượt tại B và C . Tiếp tuyến của (O) tại B và C cắt nhau tại A. Gọi H là giao điểm của OA và BC.
	a/ Chứng minh : Tam giác ABC là tam giác đều.
	b/ Chứng minh : BH2 = OH.HA
	c/ Vẽ đường kính CD của (O). Tính diện tích tam giác BCD theo bán kính R của (O)
	d/ Đường thẳng qua O và vuông góc với OB cắt AC tại F, đường thẳng qua O và vuông góc với OC cắt AB tại E. Chứng minh : EF là tiếp tuyến của (O).
C
B
A
O
H
x
D
E
F
y
4a/
Chứng minh : Tam giác ABC là tam giác đều.
Ta có AB là tiếp tuyến của (O,R)=> 
 AC là tiếp tuyến của (O,R)=> 
Ta có : AB= AC (Vì AB, AC là hai tiếp tuyến của (O) cắt nhau tại A) => ABC cân tại A (2)
Từ (1) và (2) suy ra : ABC là tam giác đều.
4b/
b/ Chứng minh : BC2 = 4OH.HA:
OBC cân tại O ( OB=OC do là bán kính của (O) )
Mà ( Do AB, AC là hai tiếp tuyến của (O) )
Nên : OABH
OBA vuông tại B, OABH=> BH2 = OH.HA
4c/
Tính diện tích tam giác BCD theo bán kính R của (O)
OBC cân tại O => 
 CD = 2R ( đvđd)
 Ta có DBC nội tiếp đường tròn (O) có CD là đường kính => DBC vuông tại B 
=> BC = CD. cosC = 2R. cos300= 2R. = R( đvđd)
 BD = CD. sinC = 2R. sin300= 2R.1/2 = R. ( đvđd)
 SBCD = BC.BD/2= R.R/2 = R2( dvdt)
4d
Chứng minh : EF là tiếp tuyến của (O).
Ta có 
OEAF là hình bình hành.
Lại có ( Do AB, AC là 2 tiếp tuyến của (O) )
OEAF là hình thoi. 
=> EFOI tại I (I là giao điểm của OA và EF) (3)
Mặt khác, ta có : 
OBA vuông tại B=> OA=OB/cosO =R/cos600 =2R.
Mà OEAF là hình thoi=> OI = OA/2 = 2R/2 = R 
=> OI là bán kính của (O) ) (4)
Từ (3) và (4) => EF là tiếp tuyến của (O).