Đề thi trung học phổ thông quốc gia năm 2016 đáp án - Thang điểm môn thi: toán

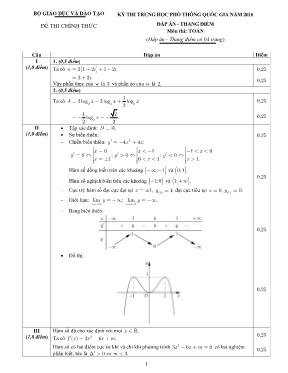
1
BỘ GIÁO DỤC VÀ ĐÀO TẠO 
ĐỀ THI CHÍNH THỨC 
KỲ THI TRUNG HỌC PHỔ THễNG QUỐC GIA NĂM 2016 
ĐÁP ÁN - THANG ĐIỂM 
Mụn thi: TOÁN 
(Đỏp ỏn - Thang điểm cú 04 trang) 
Cõu Đỏp ỏn Điểm 
I 
(1,0 điểm) 
1. (0,5 điểm) 
Ta cú w  2 1 2 1 2i i    0,25 
 3 2 .i  
Vậy phần thực của w là 3 và phần ảo của w là 2. 
0,25 
2. (0,5 điểm) 
Ta cú 
2 2 2
1
2 log 3 log log
2
A x x x   0,25 
2
1 2
log .
2 2
x   0,25 
II 
(1,0 điểm) 
 Tập xỏc định: .D   
 Sự biến thiờn: 
- Chiều biến thiờn: 34 4 ;y x x    
0,25 
0 1 1 0
0 ; 0 ; 0
1 0 1 1.
x x x
y y y
x x x
                          
 Hàm số đồng biến trờn cỏc khoảng  ; 1  và  0; 1 . 
 Hàm số nghịch biến trờn cỏc khoảng  1;0 và  1; . 
- Cực trị: hàm số đạt cực đại tại 1,x   
cđ
1;y  đạt cực tiểu tại 
CT
0, 0.x y  
- Giới hạn: lim ;
x
y

  lim .
x
y

  
0,25 
- Bảng biến thiờn: 
0,25 
 Đồ thị: 
0,25 
III 
(1,0 điểm) 
Hàm số đó cho xỏc định với mọi .x   
Ta cú 2( ) 3 6 .f x x x m    
0,25 
Hàm số cú hai điểm cực trị khi và chỉ khi phương trỡnh 23 6 0x x m   cú hai nghiệm 
phõn biệt, tức là 0 3.m    
0,25 
2
Ta cú  
2
2 2
1 2 1 2 1 2
3 2 3 4 2. 3
3
m
x x x x x x         0,25 
3
2
m  (thỏa món). Vậy 
3
.
2
m  0,25 
IV 
(1,0 điểm) Ta cú 
3 3
2 2
0 0
3 d 3 16 d .I x x x x x    0,25 
 
3
3
2 3
1 0
0
3 d 27.I x x x   0,25 
 
3
2
2
0
3 16 d .I x x x  
Đặt 2 16,t x  ta cú 2 ; (0) 16, (3) 25.t x t t    
Do đú 
25
2
16
3
d
2
I t t  
0,25 
25
16
61.t t  
Vậy 
1 2
88.I I I   
0,25 
V 
(1,0 điểm) 
Ta cú  1; 1;2 .BC  

 0,25 
Mặt phẳng ( )P đi qua A và vuụng gúc với BC cú phương trỡnh là 2 3 0.x y z    0,25 
Đường thẳng BC cú phương trỡnh là 
1
1 2 .
x t
y t
z t
    
  
 0,25 
Gọi H là hỡnh chiếu vuụng gúc của A trờn .BC Ta cú ( ) .H P BC  
- Vỡ H BC nờn  1 ; ;1 2 .H t t t   
- Vỡ ( )H P nờn      1 2 1 2 3 0t t t       1.t  
Vậy  0;1; 1 .H  
0,25 
VI 
(1,0 điểm) 
1. (0,5 điểm) 
Ta cú 2
sin 4
2 sin 7 sin 4 0 1
sin .
2
x
x x
x
  
   
 
 0,25 
 sin 4 :x   vụ nghiệm. 
 
21 6sin ( ).
52
2
6
x k
x k
x k





  

  
  

 
0,25 
2. (0,5 điểm) 
Khụng gian mẫu  cú số phần tử là 3
10
( ) A 720.n    0,25 
Gọi E là biến cố: “B mở được cửa phũng học”. Ta cú 
 (0;1;9),(0;2;8),(0;3;7),(0;4;6),(1;2;7),(1;3;6),(1;4;5),(2;3;5) .E  Do đú ( ) 8.n E  
Vậy 
( ) 1
P( ) .
( ) 90
n E
E
n
 

0,25 
3
VII 
(1,0 điểm) 
Gọi H là trung điểm của ,AC ta cú 
   o45 .A H ABC A BH    
0,25 
Ta cú 
1
2
BH AC a  và 2.
ABC
S a

 
Tam giỏc A HB vuụng cõn tại ,H suy ra 
.A H BH a   
Do đú 3
.
. .
ABC A B C ABC
V A H S a     
0,25 
Gọi I là giao điểm của A B và ,AB  ta cú I là trung điểm của A B và .AB  Suy ra 
.HI A B 
0,25 
Mặt khỏc HI là đường trung bỡnh của AB C nờn HI // .B C Do đú .A B B C  0,25 
VIII 
(1,0 điểm) 
Phương trỡnh MN: 4 0.x y   
Tọa độ P là nghiệm của hệ 
4 0 5 3
; .
1 0 2 2
x y
P
x y
               
0,25 
Vỡ AM song song với DC và cỏc điểm 
, , ,A B M N cựng thuộc một đường trũn nờn ta cú 
   .PAM PCD ABD AMP   
Suy ra .PA PM 
0,25 
Vỡ : 1 0A AC x y    nờn  ; 1 , 2.A a a a  
Ta cú 
2 2 2 2
05 5 5 5
(0; 1).
52 2 2 2
a
a a A
a
                                                  
0,25 
Đường thẳng BD đi qua N và vuụng gúc với AN nờn cú phương trỡnh là 
2 3 10 0.x y   
Đường thẳng BC đi qua M và vuụng gúc với AM nờn cú phương trỡnh là 4 0.y   
Tọa độ B là nghiệm của hệ  
2 3 10 0
1;4 .
4 0
x y
B
y
     
  
0,25 
IX 
(1,0 điểm) 
Điều kiện: 0 2.x  
Khi đú phương trỡnh đó cho tương đương với 
        2 23 3 3 33 log 2 2 4 log 2 2 .log 3 log 3 0x x x x x x         
       3 3 3 3log 2 2 log 3 3 log 2 2 log 3 0.x x x x x x                   
0,25 
    3 3log 2 2 log 3 0x x x     2 2 3x x x     
2 24 2 4 9x x    2 22 4 9 4x x    
2
4 2
4
9
81 68 0
x
x x
  
  
2 68 .
81
x  
Kết hợp với điều kiện 0 2,x  ta cú nghiệm 
2 17
.
9
x  
0,25 
    3 33 log 2 2 log 3 0x x x      
3
2 2 3 (1).x x x     
Vỡ 0 2x  nờn 3 6.x  
0,25 
4
Mặt khỏc    
2 3
22 2 4 2 4 4 2 2 8.x x x x x            Do đú 
phương trỡnh (1) vụ nghiệm. 
Vậy phương trỡnh đó cho cú nghiệm 
2 17
.
9
x  
0,25 
X 
(1,0 điểm) 
1. (0,25 điểm) 
Điều kiện: 2, 3.x y  
Ta cú    
2
(*) 1 4 1 2 2 3 (**).x y x y x y         
Vỡ 2 2 3 1x y x y     nờn từ (**) suy ra    
2
1 8 1x y x y     
1 8x y    7.x y   
Ta cú 6, 1x y  thỏa món (*) và 7.x y  Do đú giỏ trị lớn nhất của biểu thức x y 
bằng 7. 
0,25 
2. (0,75 điểm) 
Vỡ 2 2 3 0x y   nờn từ (**) suy ra    
2
1 4 1x y x y     
1 0
1 4
x y
x y
       
1 0 (vỡ 1 0)
1 4
x y x y
x y
          
1
3.
x y
x y
      
0,25 
Vỡ 2 2x x (do 2x  ), 2 1 2y y  nờn  2 2 1 2 .x y x y    Do đú 
       4 7 2 2 4 73 1 2 3 3 1 2 6 3.x y x y x y x yx y x y x y x y                   
0,25 
Đặt ,t x y  ta cú 1t   hoặc 3 7.t  
Xột hàm số  4 7( ) 3 1 2 6 3.t tf t t t      Ta cú 2188( 1) ;
243
f   
 4 7 7( ) 3 ln 3 2 1 2 ln 2 6;t t tf t t        
 4 2 7( ) 3 ln 3 1 ln 2 2 2 ln2 0, [3;7].t tf t t t            
Suy ra ( )f t đồng biến trờn (3;7). Mà ( )f t liờn tục trờn [3;7] và (3) (7) 0,f f   do đú 
( ) 0f t  cú nghiệm duy nhất 
0
(3;7).t  
Bảng biến thiờn 
Suy ra    4 7 2 2 1483 1 2 3
3
x y x yx y x y         với mọi ,x y thỏa món (*). 
Đẳng thức xảy ra khi 2, 1.x y  
Vậy 
148
.
3
m  
0,25 
--------- Hết ---------