Bài tập Hình 8 chương I: Tứ giác

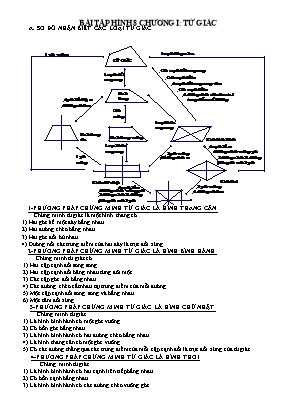
BÀI TẬP HÌNH 8 CHƯƠNG I: TỨ GIÁC
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TỨ GIÁC
 1-PHƯƠNG PHÁP CHỨNG MINH TỨ GIÁC LÀ HÌNH THANG CÂN
 Chứng minh tứ giác là một hình thang cĩ
 1) Hai gĩc kề một đáy bằng nhau .
 2) Hai đường chéo bằng nhau .
 3) Hai gĩc đối bù nhau .
 4) Đường nối các trung điểm của hai đáy là trục đối xứng .
 2-PHƯƠNG PHÁP CHỨNG MINH TỨ GIÁC LÀ HÌNH BÌNH HÀNH
 Chứng minh tứ giác cĩ
 1) Hai cặp cạnh đối song song .
 2) Hai cặp cạnh đối băng nhau từng đơi một .
 3) Các cặp gĩc đối bằng nhau .
 4) Các đường chéo cắt nhau tại trung điểm của mỗi đường .
 5) Một cặp cạnh đối song song và bằng nhau .
 6) Một tâm đối xứng .
 3-PHƯƠNG PHÁP CHỨNG MINH TỨ GIÁC LÀ HÌNH CHỮ NHẬT
 Chứng minh tứ giác
 1) Là hình bình hành cĩ một gĩc vuơng .
 2) Cĩ bốn gĩc bằng nhau .
 3) Là hình bình hành cĩ hai đường chéo bằng nhau .
 4) Là hình thang cân cĩ một gĩc vuơng .
 5) Cĩ các đường thẳng qua các trung điểm của mỗi cặp cạnh đối là trục đối xứng của tứ giác
 4-PHƯƠNG PHÁP CHỨNG MINH TỨ GIÁC LÀ HÌNH THOI
 Chứng minh tứ giác
 1) Là hình bình hành cĩ hai cạnh liên tiếp bằng nhau .
 2) Cĩ bốn cạnh bằng nhau .
 3) Là hình bình hành cĩ các đường chéo vuơng gĩc .
 4) Cĩ mỗi đường chéo là phân giác của gĩc cĩ đỉnh thuộc đường chéo đĩ .
 5) Là hình bình hành cĩ một đường chéo là phân giác của một gĩc cĩ đỉnh thuộc đường chéo ấy .
 6) Cĩ mỗi đường thẳng qua hai đỉnh đối nhau là một trục đối xứng của nĩ .
 5-PHƯƠNG PHÁP CHỨNG MINH TỨ GIÁC LÀ HÌNH VUƠNG
 Chứng minh tứ giác
 1) Là hình thoi cĩ một gĩc vuơng .
 2) Là hình chữ nhật cĩ hai cạnh liên tiếp bằng nhau .
 3) Là hình thoi cĩ hai đường chéo bằng nhau .
 4) Là hình chữ nhật cĩ hai đường chéo vuơng gĩc .
 5) Cĩ bốn trục đối xứng là các đường thẳng qua các đỉnh đối nhau , các đường thẳng qua trung điểm các cạnh đối nhau .
B. MỘT SỐ KIẾN THỨC LIÊN QUAN
1. Tính chất của các hình: hình thang, hình thang cân, hình bình hành, hình chữ nhật, hình thoi, hình vuơng.
2. Đường trung bình của tam giác; hình thang:
 a. Định nghĩa:
 Đường trung bình của tam giác là đọn thẳng nối trung điểm hai cạnh của tam giác.
 Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
 b. Các tính chất:
 Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
 Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
 Định lí 3 :Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
 Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
3. Đối xứng trục; đối xứng tâm:
 Hai điểm gọi là đối xứng nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đĩ.
 Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điếm của đoạn thẳng nĩi hai điêm đĩ 
4. Áp dụng vào tam giác:
 Trong một tam giác vuơng, đương trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
 Nếu một tam giác cĩ đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đĩ là tam giác vuơng.
C. MỘT SỐ BÀI TẬP CƠ BẢN TRONG SÁCH GIÁO KHOA:
Bài 48 SGK T93
 Tứ giác ABCD cĩ E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
( với bài tồn này các em co thể thay đổi đề bài bằng cách M, N, P, Q là trung điểm của hai cạnh, hai đường chéo thì cũng chứng minh tương tự ).
Bài 49 SGK T93 
 Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD và AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
AI // CK
DM = MN = NB.( câu hỏi cĩ thể thay đổi là chứng minh AI, CK chia BD thành ba phần bằng nhau)
Bài 64 SGK T100
 Cho hình bình hành ABCD. Các tia phân giác của các gĩc A, B, C, D đơi một cắt nhau tại G, F, E, H. Chứng minh: EFGH là hình chữ nhật.
Bài 65 SGKT100
 Tứ giác ABCD cĩ hai đương chéo vuơng gĩc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
Bài 76 SGK T106
 Chứng minh rằng các trung điểm của bốn cạnh của hình thoi là các đỉnh của một hình chữ nhật.
Bài 84 SGK T109
 Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường song song với AB và AC, chúng cắt các cạnh Acvà AB theo thứ tự ở E và F.
Tứ giác AEDF là hình gỉ? Vì sao?
Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?
Nếu tam giác ABC vuơng tại A thì tứ giác AEDF là hình gì? Vì sao?
Bài 85 SGK T109
 Cho hình chữ nhật ABCD cĩ AB = 2CD, Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
 Tứ giác ADFE là hình gì? Vì sao?
Tứ giác EMFN là hình gì? Vì sao? 
Bài 88 SGK T111
 Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD cĩ điều kiện gì thì ÈGH là:
 Hình chữ nhật?
Hình thoi?
 Hình vuơng?
Bài 89 SGK T109
 Cho tam giác ABC vuơng tại A, trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
Chứng minh rằng điểm E đối xứng với điểm M qua AB.
Các tứ giác AEMC, AEBM là hình gì? Vì sao?
Cho BC = 4cm. Tính chu vi tứ giác AEBM.
Tam giác vuơng ABC cĩ thêm điều kiện gì thì AEBM là hình vuơng?
Nhận xét
 Bài 48 và 65 cĩ họ với nhau, cịn các bài 84c, 88, 89d học sinh rất lúng túng và khĩ giải quyết. Sau đây là một số ví dụ liên quan 
*Tơi xin minh hoạ 1 số trường hợp cụ thể bằng các bài tốn sau . Lời giải trình bày gọn , chủ yếu là gợi ý. HS hiểu và làm lại chi tiết hơn .
Ví dụ 1 : Đường chéo của tứ giác cho trước thay đổi dẫn đến tứ giác khác thay đổi loại hình .
 Cho tứ giác ABCD, gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB,BC,CD,DA.
Chứng minh tứ giác MNPQ là hình bình hành
Tứ giác ABCD phải thoả điều kiện gì về đường chéo để : MNPQ là hình chữ nhật, hình thoi , hình vuơng ?
 * Giải : 
a) Vẽ 2 đường chéo AC,BD
 Ta cĩ : (tính chất đường trung bình của tam giác )
 Vậy MNPQ là hình bình hành .
 b)- MNPQ là hình chữ nhật thì = 1v
 - MNPQ là hình thoi thì MN = MQ
 - MNPQ là hình vuơng thì và AC = BD
Ví dụ 2 :Vị trí điểm trên cạnh tam giác và tam giác cho trước thay đổi loại hình dẫn đến tứ giác thay đổi loại hình .
 Cho,D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song AB và AC. Chúng cắt các cạnh AC , AB theo thứ tự tại E và F .
 a) Tứ giác AEDF là hình gì ? Vì sao ?
 b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi ?
 c)Nếuvuơng tại A thì tứ giác AEDF là hình gì ? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuơng ?
 * Giải :
 a) Ta cĩ : (gt)	
	 (gt) Vậy AEDF là hình bình hành .
 b)Vẽ đường chéo AD
 Để AEDF là hình thoi thì AD là phân giác Â
 Vậy D là giao điểm của phân giác  và BC
 c) Nếu thì AEDF là hình chữ nhật
 Để AEDF là hình vuơng thì : Â = 1v và AD là phân giácÂ
Ví dụ 3 : Khi tứ giác cho trước thay đổi loại hình dẫn đến tứ giác khác thay đổi loại hình .
 Cho tứ giác ABCD . Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
 a) Chứng minh tứ giác MNPQ là hình bình hành .
 b) Nếu ABCD là hình bình hành thì MNPQ là hình gì ? Vì sao ?
 Nếu ABCD là hình thoi thì MNPQ là hình gì ? Vì sao ?
 Nếu ABCD là hình chữ nhật thì MNPQ là hình gì ? Vì sao ?
 Nếu ABCD là hình vuơng thì MNPQ là hình gì ? Vì sao ?
* Giải :
 a) (Xem bài 1 phần a )
 b) Nếu ABCD là hình bình hành thì MNPQ là hình bình hành (tương tự phần a)
 Nếu ABCD là hình chữ nhật thì : AC = BD thì MNPQ là hình thoi .
 Nếu ABCD là hình thoi thì : hay = 1v thìMNPQ là hình chữ nhật . Nếu ABCD là hình vuơng thì : MN = MQ và = 1v thì MNPQ là hình vuơng .
Ví dụ 4 :Khi hình thang cho trước thay đổi loại hình và gĩc dẫn đến tứ giác thay đổi loại hình .
 Cho hình thang ABCD (). Gọi M,N,P,Q là trung điểm các cạnh AB, AC, DC, BD .
 a) Chứng minh tứ giác MNPQ là hình bình hành .
 b) Nếu ABCD là hình thang cân thì MNPQ là hình gì ?
 c) Khi MNPQ là hình vuơng . Tính các gĩc của hình thang ABCD.
 Giải :
 a) Ta cĩ : ( tính chất đường trung bình của tam giác )
 Vậy MNPQ là hình bình hành
 b) Nếu ABCD là hình thang cân thì AD = BC 
 Vậy MNPQ là hình thoi .
 c) Khi MNPQ là hình vuơng thì = 1v hay
	 nên = = 450 Do đĩ Â = = 1350
Ví dụ 5 : Khi tam giác cho trước thay đổi loại hình dẫn đến các tứ giác thay đổi loại hình .
 * Cho cân tại A . Gọi M,N,P thứ tự là trung điểm các cạnh AB, AC, BC . Q là điểm đối xứng của P qua N .
 a) Chứng minh tứ giác PMAQ là hình thang .
 b) Chứng minh tứ giác APCQ là hình chữ nhật .
 c)phải thoả mãn điều kiện gì để các tứ giác PMAQ là hình thang cân , APCQ là hình vuơng .
 Giải :
 a) Ta cĩ : (tính chất đường trung bình của tam giác )
 hay Vậy PMAQ là hình thang
 b) Ta cĩ NA = NC (gt)
	 NP = NQ ( tính chất đối xứng)
 cân tại A nên AP cũng là đường cao , do đĩ ; hay = 1v
 Vậy APCQ là hình chữ nhật .
 c) - Nếu PMAQ là hình thang cân thì Q = P mà Q = B (gĩc đối hình bình hành)
	 P = A (gĩc đối hình thoi )
 Do đĩ : Â = Vậy đều 
	- Nếu APCQ là hình vuơng thì AP = PC (=) 
	Vậy vuơng cân tại A
 Ví dụ 6:Khi tam giác cho trước thay đổi loại hình và gĩc giữa 2 trung tuyến thay đổi dẫn đến tứ giác thay đổi loại hình .
 * Cho . Các đường trung tuyến BE và CF cắt nhau tại G . Gọi I,J là trung điểm GB, GC .
 a) Chứng minh tứ giác EFIJ là hình bình hành .
 b) phải cĩ điều kiện gì để tứ giác EFIJ là hình chữ nhật ?
 c) Nếu thì tứ giác EFIJ là hình gì ?
Giải :
 a) Ta cĩ : (tính chất đường trung bình của tam giác)
 Vậy EFIJ là hình bình hành .
 b) Để EFIJ là hình chữ nhật thì FJ = IE . Do đĩ BE = CF .
 Vậy cân tại A
 c) Nếu hay Vậy EFIJ là hình vuơng .
D. BÀI TẬP TỰ LUYỆN
Bài 1: Cho hình bình hành ABCD cĩ BC = 2AB và gĩc A = 600. Gọi E, F theo thứ tự là trung đIểm của BC và AD.
Tứ giác ECDF là hình gì?
Tứ giác ABED là hình gì? Vì sao?
Tính số đo của gĩc AED.
Bài 2: Cho DABC. Gọi M, N lần lượt là trung điểm của BC, AC. Gọi H là điểm đối xứng của N qua M.
a) C/m tứ giác BNCH và ABHN là hình bình hành.
b) DABC thỏa mãn điều kiện gì thì tứ giác BCNH là hình chữ nhật.
Bài 3: Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đĩ cắt nhau ở K.
Chứng minh tứ giác OBKC là hình chữ nhật
Chứng minh AB = OK
Tìm điều kiện của hình thoi ABCD để tứ giác OBKC là hình vuơng?
Bài 4: Cho tứ giác ABCD. Gọi O là giao điểm của 2 đường chéo (khơng vuơng gĩc), I và K lần lượt là trung điểm của BC và CD. Gọi M và N theo thứ tự là điểm đối xứng của điểm O qua tâm I và K.
a) C/m rằng tứ giác BMND là hình bình hành.
b) Với điều kiện nào của hai đường chéo AC và BD thì tứ giác BMND là hình chữ nhật.
c) Chứng minh 3 điểm M, C, N thẳng hàng.
Bài 5: Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của AD và BC. Đường chéo AC cắt các đoạn thẳng BE và DF theo thứ tự tại P và Q.
a) C/m tứ giác BEDF là hình bình hành.
b) Chứng minh AP = PQ = QC.
c) Gọi R là trung điểm của BP. Chứng minh tứ giác ARQE là hình bình hành.
Bài 6: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình vuơng?
c) Với điều kiện câu b) hãy tính tỉ số diện tích của tứ giác ABCD và MNPQ
Bài 7: Cho DABC, các đường cao BH và CK cắt nhau tại E. Qua B kẻ đường thẳng Bx vuơng gĩc với AB. Qua C kẻ đường thẳng Cy vuơng gĩc với AC. Hai đường thẳng Bx và Cy cắt nhau tại D.
a) C/m tứ giác BDCE là hình bình hành.
b) Gọi M là trung điểm của BC. Chứng minh M cũng là trung điểm của ED.
c) DABC phải thỏa mãn đ/kiện gì thì DE đi qua A
Bài 8: Cho hình thang cân ABCD (AB//CD), E là trung điểm của AB.
a) C/m: D EDC cân 
b) Gọi I,K,M theo thứ tự là trung điểm của BC, CD, DA. Tứ giác EIKM là hình gì? Vì sao?
c) Tính S ABCD, SEIKM biết EK = 4, IM = 6.
Bài 9: Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AB và CD.
a) Tứ giác DEBF là hình gì? Vì sao?
b) C/m 3 đường thẳng AC, BD, EF đồng qui.
c) Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh tứ giác EMFN là hình bình hành.
d) Tính SEMFN khi biết AC = a, BC= b, AC BD
Bài 10: Cho hình thang cân ABCD (AB//CD) và CD = 2AB. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CD và AD.
Chứng minh tứ giác ABCN là hình bình hành ?
b/ Gọi O là giao điểm của AC và BN. Chứng minh ba điểm P, O, M thẳng hàng. c) Chứng minh: PO = 2OM
Bài 11: Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đĩ cắt nhau ở K
Chứng minh tứ giác OBKC là hình chữ nhật b)Chứng minh AB = OK
c) Tìm điều kiện của hình thoi ABCD để tứ giác OBKC là hình vuơng?
Bài 12: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, M là giao điểm của AB và DH , gọi E là điểm đối xứng với H qua AC, N là giao điểm của AC và HE.
 a./ Chứng minh tứ giác AMHN là hình chữ nhật .
 b./ Chứng minh rằng D đối xứng với E qua A.
 c./ Tìm điều kiện của tam giác ABC để tứ giác AMHN là hình vuông.
Bài 13: Cho tam giác ABC vuông tại A. Gọi M và D lần lượt là trung điểm của BC và AC; E là điểm đối xứng với M qua D.
Tứ giác AEMB và AECM là hình gì ? vì sao?
Tam giác vuông ABC có điều kiện gì thì AECM là hình vuông.
Bài 14. Cho tam giác ABC cĩ M là điểm nằm giữa B và C . Qua M kẻ các đường thẳng song song với AB và AC , chúng cắt các cạnh AC và AB theo thứ tự tại P và Q. Gọi N là trung điểm của cạnh PQ .
Chứng minh tứ giác APMQ là hình bình hành .
Chứng minh ba điểm A ,N , M thẳng hàng . Khi M di chuyển trên cạnh BC thì N di chuyển trên đường nào 
Điểm M ở vị trí nào trên cạnh BC thì tứ giác APMQ là hình thoi
Bài 15. Cho hình bình hành ABCD cĩ 2AB = BC = 2a,.Gọi M, N lần lượt là trung điểm của AD và BC.
Tứ giác AMNB là hình gì ? Vì sao? 
Chứng minh rằng: AN ^ ND ; AC = ND
Tính diện tích của tứ giác AMNB và tam giác AND theo a
Bài 16. Cho tam giác ABC vuơng tại A cĩ . Trên nửa mặt phẳng cĩ bờ là đường thẳng AB (chứa điểm C) kẻ tia Ax // BC. Trên Ax lấy điểm D sao cho AD = DC.
	a. Tính các gĩc BAD; ADC
	b. Chứng minh tứ giác ABCD là hình thang cân
	c. Gọi M là trung điểm của BC. Tứ giác ADMB là hình gì? Tại sao?
	d. So sánh diện tích của tứ giác AMCD với diện tích tam giác ABC
Bài 17. Cho tam giác ABC cĩ H là trực tâm. Qua B kẻ Bx vuơng gĩc với BA, qua C kẻ Cy vuơng gĩc với CA. Gọi D là giao điểm của Bx và Cy, N là giao điểm của AH và BC.
Chứng minh tứ giác BDCH là hình bình hành;
Gọi M là trung điểm của BC. Chứng minh H và D đối xứng nhau qua M. 
Tìm điều kiện của tam giác ABC để ba điểm A, D, H thẳng hàng;
Giả sử H là trung điểm của AN. Chứng minh rằng SABC = SBDCH
Bài 18. Cho tứ giác ABCD . Gọi M, N, E, F lần lượt là trung điểm của AB, BC, CD và DA . Hai đường chéo AC và BD thỏa mãn điều kiện gì thì :
Tứ giác MNEF là hình vuơng .
Khi AC = 4 cm . Tính chu vi và diện tích hình vuơng MNEF.
Bài 19. Cho tứ giác ABCD . Hai đường chéo AC và BD vuơng gĩc với nhau . Gọi M,N, P, Q lần lược là trung điểm các cạnh AB ;BC; CD ;DA . 
Tứ giác MNPQ là hình gì ?
b. Cho AC = 4cm , BD = 8cm . Tính SABCD = ?
Để MNPQ là hình vuơng thì tứ giác ABCD cần cĩ điều kiện gì ? 
Bài 20:
 1. Cho tam giác ABC vuơng tại A, AB = 15cm, AC = 20cm. Gọi M là trung điểm BC. Tính AM.
 2. Cho tam giác ABC (AB < AC) cĩ AH là đường cao. Gọi M, N, P lần lượt là trung điểm AB, AC, BC.
Chứng minh: BMNP là hình bình hành
Gọi K là điểm đối xứng của H qua M. Chứng minh: AKBH là hình chữ nhật.
Chứng minh: MNPH là hình thang cân.
Gọi O là điểm đối xứng của H qua AB. Chứng minh: OK ^ OH
Bài 21:
 1.Cho tứ giác ABCD cĩ . Tính số đo gĩc C và gĩc D.
 2. Cho tam giác ABC vuơng tại A (AB<AC). Gọi M là trung điểm BC. D, E lần luợt là hình chiếu của M lên AB và AC.
Chứng minh: ADME là hình chữ nhật.
Chứng minh: BDEM là hình bình hành.
Gọi O là giao điểm của BE và DM, I là trung điểm của EC. Chứng minh: AOMI là hình thang cân.
Vẽ đường cao AH của DABC. Tính số đo gĩc DHE.
Bài 22: 
 1. Cho hình thang ABCD cĩ . Tính các gĩc của hình thang này.
 2. Cho DABC cân tại A. M, N, H lần lượt là trung điểm AB, AC và BC. AH cắt MN tại O.
Chứng minh: BMNC là hình thang cân
Chứng minh: AMHN là hình thoi
Gọi K là điểm đối xứng của H qua N. Chứng minh: B, O, K thẳng hang.
BK cắt AC tại D. Chứng minh: AB = 3 AD.
Bài 23: Cho tam giác ABC cĩ I, H, K lần lượt là trung điểm AB, BC, AC.
Chứng minh: IK là đường trung bình của DABC.
Chứng minh: BIKH là hình bình hành.
Bài 24: Cho hình bình hành ABCD cĩ AB = 2AD. Gọi E, F lần lượt là trung điểm AB, CD.
Chứng minh: AECF là hình bình hành.
Chứng minh: AEFD là hình thoi.
AF cắt DE tại R; CE cắt BF tại S. Chứng minh: ERFS là hình chữ nhật.
Gọi I và K lần lượt là giao điểm của BD với AF và CE. Chứng minh D EIK cân.
Bài 25: Cho hình thoi ABCD (AC > BD) biết AC = 24cm, BD = 18cm. Tính chu vi hình thoi ABCD
Bài 26: Cho hình vuơng ABCD cĩ hai đường chéo cắt nhau tai O. M, N, P lần lượt là trung điểm AO, OB và CD.
Chứng minh: AMNB là hình thang cân.
Chứng minh: MNPD là hình bình hành.
Chứng minh: DM ^ AN.
Gọi I là trung điểm AP . Chứng minh D DIN cân.
Bài 27: Cho tam giác ABC cĩ AB = 5cm, AC = 12cm, BC = 13cm. Gọi I và K lần lượt là trung điểm AB và BC. Tính IK, AK.
Bài 28: Cho hình bình hành ABCD có M là trung điểm AB và N là trung điểm CD.
Chứng minh : tứ giác AMND là hình bình hành.
 Chứng minh : tứ giác AMCN là hình bình hành.
 Chứng minh : AC, BD, MN đờng quy. 
 Hình bình hành ABCD có điều kiện gì thì tứ giác AMND là hình chữ nhật, hình thoi, hình vuơng.
E. BÀI TẬP VỀ ĐIỀU KIỆN :
 1. Cho, đường trung tuyến AM . Gọi I là trung điểm AC , D là điểm đối xứng với M qua I .
 a) Tứ giác AMCD là hình gì ? Vì sao ?
 b) Nếu cĩ Â = 900 thì tứ giác AMCD là hình gì ? Vì sao ?
 c) Tìm điều kiện của để AMCD là hình vuơng ?
 2. Cho hình bình hành ABCD . Trên đường chéo BD lấy E,K sao cho BE = DK .
 a) Chứng minh AKCE là hình bình hành .
 b) Hình bình hành ABCD cĩ thêm điều kiện gì để AKCE là hình thoi ?
 3. Cho hình thoi ABCD . Gọi O là giao điểm của AC và BD . Vẽ đường thẳng qua B và song song AC , vẽ đường thẳng qua C và song song BD . Hai đường đĩ cắt nhau tại K .
 a)Tứ giác OBKC là hình gì ? Vì sao ?
 b) Tìm điều kiện của hình thoi ABCD để OBKC là hình vuơng ?
 4. Cho tứ giác ABCD , các phân giác các gĩc Â, B,C,D cắt nhau tại M,N P,Q .
 a) Chứng minh tứ giác MNPQ cĩ tổng các gĩc đối bù nhau . 
 b) Nếu ABCD là hình bình hành thì MNPQ là hình gì ? Vì sao ?
 c) Nếu ABCD là hình chữ nhật thì MNPQ là hình gì ? Vì sao ?
 d) Nếu ABCD là hình thoi , hình vuơng thì MNPQ là hình gì ? Vì sao ?
 5. Cho hình bình hành ABCD . Gọi E,F là trung điểm AB, CD . AF cắt BC tại G , BF cắt AD tại H.
 a) Chứng minh ABGH là hình thoi .
 b) Hình bình hành ABCD cĩ thêm điều kiện gì để ABGH là hình vuơng ?
 6. Cho hình thang ABCD () . Gọi M,N,P,Q lần lượt là trung điểm các cạnh AB, BC, CD , DA .
 a) Chứng minh tứ giác MNPQ là hình bình hành .
 b) Với điều kiện nào của hình thang ABCD thì MNPQ là hình thoi , hình vuơng .
 7. Cho, gọi D,E,F lần lượt là trung điểm của các cạnh AB, AC, BC . gọi M,N,P,Q là trung điểm AD, AE, EF, FD .
 a) Chứng minh các tứ giác ADFE, MNPQ là hình bình hành .
 b) Khi cĩ A = 1v thì ADFE, MNPQ là hình gì ? Vì sao ?
 8. Cho cĩ AA’, BB’,CC’ là các trung tuyến , Trọng tâm G . Trên tia đối của tia B’G lấy D sao cho B’D = B’G . Trên tia đối của tia C’G lấy E sao cho C’E = C’G .
 a) Chứng minh BEDC là hình bìng hành .
 b) Tìm điều kiện của để BEDC là hình chữ nhật ?
 c) Tứ giác BEDC cĩ thể là hình vuơng , hình thoi được khơng ? Vì sao ?
 9. Cho và H là trực tâm . Các đường thẳng vuơng gĩc với AB tại B , vuơng gĩc với AC tại C cắt nhau ở D .
 a) Chứng minh tứ giác BDCH là hình bình hành .
 b) Nếu cĩ Â = 1v thì BDCH là hình gì ?
 c) Tìm điều kiện của để BDCH là hình thoi ?
 10. Cho hình bình hành ABCD . Gọi M,N,P,Q là trung điểm của các cạnh AB, BC, CD ,DA . Nối AN, BP, CQ, DM chúng cắt nha