Bài tập Đại số 11 - Chương 1: Hàm số lượng giác và phương trình lượng giác

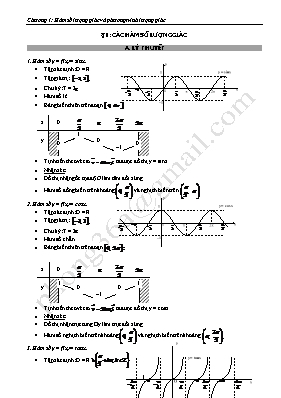
§1: CÁC HÀM SỐ LƯỢNG GIÁC
A. LÝ THUYẾT
1. Hàm số y = f(x) = sinx.
Tập xác định: D = R.
Tập giá trị: 
Chu kỳ: T = 2p.
Hàm số lẻ
Bảng biến thiên trên đoạn 
x
0
y
1
0
–1
0
0
Tịnh tiến theo véctơ ta được đồ thị y = sinx.1
0
p
2p
y = sinx
–1
y 
x
Nhận xét:
Đồ thị nhận gốc tọa độ O làm tâm đối xứng.
1
0
p
2p
y = cosx
–1
y 
x
Hàm số đồng biến trên khoảng và nghịch biến trên 
2. Hàm số y = f(x) = cosx.
Tập xác định: D = R.
Tập giá trị: 
Chu kỳ: T = 2p.
Hàm số chẵn
Bảng biến thiên trên đoạn 
x
0
y
0
–1
0
1
1
Tịnh tiến theo véctơ ta được đồ thị y = cosx.
Nhận xét:
Đồ thị nhận trục tung Oy làm trục đối xứng.
x
y
O
y = tanx
Hàm số nghịch biến trên khoảng và nghịch biến trên khoảng 
3. Hàm số y = f(x) = tanx.
Tập xác định: D = R
Tập giá trị: R.
Giới hạn: 	 là tiệm cận đứng.
Chu kỳ: T = p.
Hàm số lẻ
x
0
y
0
–¥
+¥
Bảng biến thiên trên :
Tịnh tiến theo véctơ ta được đồ thị y = tanx.
Nhận xét:
Đồ thị nhận gốc tọa độ O làm tâm đối xứng.
Hàm số luôn đồng biến trên tập xác định D.
x
y
O
y = cotx
4. Hàm số y = f(x) = cotx.
Tập xác định: D = R
Tập giá trị: R.
Giới hạn: 
tiệm cận đứng: x = 0, x = p.
Chu kỳ: T = p.
Hàm số lẻ
Bảng biến thiên trên đoạn :
x
0
y
0
+¥
–¥
Tịnh tiến theo véctơ ta được đồ thị y = cotx.
Nhận xét:
Đồ thị nhận gốc tọa độ O làm tâm đối xứng.
Hàm số luôn giảm trên tập xác định D. 
B. CÁC DẠNG BÀI TẬP:
Dạng 1: Tìm tập xác định của hàm số lượng giác
Ví dụ 1: Tìm tập xác định của các hàm số
	a) 	b) 	c) 	
d) 
Ví dụ 2: Tìm tập xác định của các hàm số
	a) 	b) 
Dạng 2: Xét tính chẵn, lẻ của các hàm số lượng giác
Ví dụ 1: Xét tính chẵn, lẻ của các hàm số
	a) 	b) 	c) 	d) 
Ví dụ 2: Xác định giá trị của m sao cho:
Hàm số là hàm số chẵn
Hàm số là hàm số lẻ.
Dạng 3: Xét chiều biến thiên của hàm số lượng giác
Ví dụ 1: Không sử dụng máy tính, hãy so sánh các giá trị lượng giác sau đây:
	a) và 	b) và 	
Ví dụ 2: Xét chiều biến thiên của các hàm số sau đây trên đoạn, khoảng chỉ ra:
	a) 	b) 
Ví dụ 3: Chứng minh rằng: 
	a) khi 	b) khi 
Dạng 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác 
Phương pháp: 
- Dựa vào bảng biến thiên của hàm số lượng giác
- Dựa vào tính chất của HSLG (tập GT)
- Dựa vào các BĐT: Cosi, Bunhiacopxki, BĐT về giá trị tuyệt đối.
Ví dụ 1: Cho hàm số . Tìm GTLN và GTNN của hàm số trên 
Ví dụ 2: Tìm GTLN và GTNN của các hàm số:
	a) 	b) 	c) 
Dạng 5: Xét tính tuần hoàn của hàm số lượng giác
Phương pháp:
Nhận xét: 
	- Các hàm số tuần hoàn với chu kì 
	- Các hàm số tuần hoàn với chu kì 
Ví dụ 1: Chứng minh rằng hàm số sau là tuần hoàn và tìm chu kì của nó: 
Dạng 6: Đồ thị của hàm số lượng giác
1. Vẽ đồ thị hàm số lượng giác:
–	Tìm tập xác định D.
–	Tìm chu kỳ T0 của hàm số.
–	Xác định tính chẵn – lẻ (nếu cần).
–	Lập bảng biến thiên trên một đoạn có độ dài bằng chu kỳ T0 có thể chọn:
	 hoặc .
–	Vẽ đồ thị trên đoạn có độ dài bằng chu kỳ.
– Rồi suy ra phần đồ thị còn lại bằng phép tịnh tiến theo véc tơ về bên trái và phải song song với trục hoành Ox (với là véc tơ đơn vị trên trục Ox).
2. Một số phép biến đổi đồ thị:
a/	Từ đồ thị hàm số y = f(x), suy ra đồ thị hàm số y = f(x) + a bằng cách tịnh tiến đồ thị y = f(x) lên trên trục hoành a đơn vị nếu a > 0 và tịnh tiến xuống phía dưới trục hoành a đơn vị nếu a < 0.
b/	Từ đồ thị y = f(x), suy ra đồ thị y = –f(x) bằng cách lấy đối xứng đồ thị y = f(x) qua trục hoành.
c/	Đồ thị được suy từ đồ thị y = f(x) bằng cách giữ nguyên phần đồ thị y = f(x) ở phía trên trục hoành và lấy đối xứng phần đồ thị y = f(x) nằm ở phía dưới trục hoành qua trục hoành.
Ví dụ 1: Cho hàm số 
Lập bảng biến thiên của hàm số trên đoạn 
Vẽ đồ thị của hàm số đã cho.
Ví dụ 2: Cho hàm số 
Lập bảng biến thiên của hàm số trên đoạn 
Vẽ đồ thị (C) của hàm số đã cho.
Từ đồ thị (C) hãy suy ra đồ thị (C’) của hàm số 
C. BÀI TẬP ÔN LUYỆN
Tập xác định của hàm số lượng giác
Bài 1: Các khẳng định sau đây đúng hay sai:
Hàm số có tập xác định là R
Hàm số có tập xác định là R
Hàm số xác định với mọi x khác 0
Bài 2: Tìm tập xác định của các hàm số sau:
a) 	b) 
c) 	d) 
Bài 3: Tìm tất cả giá trị của m để hàm số có tập xác định là R.
Tính chẵn lẻ, của hàm số lượng giác
Bài 4: Xét tính chẵn lẻ của các hàm số sau:
	a) 	b) 
	c) 	d) 
Bài 5: Xét tính chẵn lẻ của các hàm số sau:
	a) 	b) 
Bài 6: Cho hàm số . Chứng minh rằng với mọi số nguyên dương n ta đều có:
Chiều biến thiên của hàm số lượng giác
Bài 7: Hãy điền các từ đồng biến , nghịch biến vào cột chiều biến thiên
Hàm số
Khoảng
Chiều biến thiên
Bài 8: So sánh các giá trị lượng giác ( không sử dụng máy tính ):
	a) và 	b) và 
	c) và 	d) và 
Bài 9: xét chiều biến thiên của các hàm số sau đây trên khoảng hoặc đoạn chỉ ra:
	a) trên 	b) trên 
	c) trên 	d) trên 
Bài 10: Cho tam giác ABC với . Khẳng định nào sau đây đúng:
	a) 	b) 
	b) 	d) 
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác
Bài 11: Tìm GTNN và GTLN của hàm số lượng giác
	a) 	b) 
Bài 12: Tìm GTNN của các hàm số:
	a) với 
	b) với 
Bài 13: Cho hàm số .
Xét chiều biến thiên của hàm số trên đoạn 
Tìm GTLN và GTNN của hàm số trên đoạn 
Chu kỳ của các hàm số lượng giác
Bài 14: Tìm chu kì của các hàm số: 
	a) 	b) 
	c) 	d) 
Bài 15: Cho hàm số . Chứng minh rằng với mọi x và mọi số nguyên k.
Đồ thị của hàm số lượng giác
Bài 16: 
Vẽ đồ thị (C) của hàm số 
Suy ra đồ thị (C1) và (C2) của các hàm số 
Bài 17: Từ đồ thị của hàm số hãy suy ra đồ thị của các hàm số:
	a) 	b) 
§2: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
A. LÝ THUYẾT:
1.	Phương trình sinx = sin
	a/	
	b/	
	c/	
	d/	
	e/ 	
Các trường hợp đặc biệt:
2.	Phương trình cosx = cos
	a/	
	b/	
	c/	
	d/	
	e/	
Các trường hợp đặc biệt:
3.	Phương trình tanx = tan
	a/	
	b/	
	c/	
	d/	 
	e/ 	
Các trường hợp đặc biệt:
4.	Phương trình cotx = cot
Các trường hợp đặc biệt:
5.	Một số điều cần chú ý:
	a/	Khi giải phương trình có chứa các hàm số tan, cot, có mẫu số hoặc chứa căn bậc chẵn, thì nhất thiết phải đặt điều kiện để phương trình xác định.
	*	Phương trình chứa tanx thì điều kiện: 
	*	Phương trình chứa cotx thì điều kiện: 
	*	Phương trình chứa cả tanx và cotx thì điều kiện 
	*	Phương trình có mẫu số:
	·	
	·	
	·	
	·	
	b/	Khi tìm được nghiệm phải kiểm tra điều kiện. Ta thường dùng một trong các cách sau để kiểm tra điều kiện:
	1.	Kiểm tra trực tiếp bằng cách thay giá trị của x vào biểu thức điều kiện.
	2.	Dùng đường tròn lượng giác.
	3.	Giải các phương trình vô định.
B. CÁC DẠNG BÀI TẬP:
Dạng 1: Phương trình lượng giác cơ bản
Ví dụ 1: Giải các phương trình sau:
	a) 	b) 
	c) 	d) 
Ví dụ 2: Giải các phương trình sau: 
	a) 	b) 
	c) 
Ví dụ 3: Giải phương trình 
Dạng 2: Giải phương trình lượng giác cơ bản thỏa mãn điều kiện cho trước
Ví dụ 1: Giải các phương trình sau với điều kiện đã chỉ ra:
 với 	b) với 
Ví dụ 2: Tìm nghiệm của phương trình sau với điều kiện đã chỉ ra
	a) 	b) với 
Dạng 3: Tìm điều kiện để phương trình có nghiệm
Ví dụ 1: xác định các giá trị của m phương trình để các phương trình sau có nghiệm
	a) 	b) 
C. BÀI TẬP LUYỆN TẬP
Phương trình lượng giác cơ bản
Bài 1: Giải các phương trình sau đây
	a) 	b) 
	c) 	d) 
Bài 2: Giải các phương trình sau
	a) 	b) 
	c) 	d) 
Bài 3: Giải các phương trình sau:
	a) 	b) 
	c) 	d) 
Bài 4: Giải các phương trình sau bằng cách sử dụng công thức hạ bậc
	a) 	b) 
	c) 	d) 
Bài 5: Gải các phương trình sau đây
	a) 	b) 
Tìm nghiệm phương trình lượng giác thỏa mãn điều kiện cho trước
Bài 6: Hãy cho biết số nghiệm của mỗi phương trình sau trong khoảng chỉ ra:
	a) trên khoảng 	b) trên khoảng 
Bài 7: Giải các phương trình sau với điều kiện của nghiệm đã chỉ ra:
	a) 	b) 
Bài 8: Giải các phương trình sau với điều kiện của nghiệm đã chỉ ra:
	a) với điều kiện 
	b) với điều kiện 
Bài 9: Giải các phương trình sau:
	a) 	b) 
Tìm điều kiện để phương trình lượng giác có nghiệm
Bài 10: Tìm m để mỗi phương trình sau đây có nghiệm:
	a) 	b) 
Bài toán lượng giác có ý nghĩa thực tế
Bài 11: Một chất điểm M chuyển động tròn đều theo hướng dương trên một đường tròn cố định tâm O, bán kính r=25 cm đặt trên mặt phẳng tọa độ Oxy. Biết tốc độ dài của chất điểm là 36km/h. Tại thời điểm t=0, chất điểm ở B.
Tìm hoành độ của chất điểm tại thời điểm t (t>0)
Xác định thời điểm chất điểm chạy đến trùng vị trí A trên đường tròn.
§3: MỘT SỐ DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC ĐƠN GIẢN
A. LÝ THUYẾT:
I. Phương trình bậc nhất và bậc hai với một hàm số lượng giác
1. Phương trình bậc nhất với một hàm số lượng giác:
2. Phương trình bậc hai với một hàm số lượng giác: 
Dạng
Đặt
Điều kiện
t = sinx
t = cosx
t = tanx
t = cotx
Nếu đặt: 
II. Phương trình bậc nhất đối với sinx và cosx
1. Dạng: a sinx + b cosx = c (1)
2. Cách giải:
Cách 1:
·	Chia hai vế phương trình cho ta được: 
(1) Û 
·	Đặt: 
	phương trình trở thành: 	
·	Điều kiện để phương trình có nghiệm là: 
·	(2) 
Cách 2: 
a/	Xét có là nghiệm hay không?
b/	Xét 
Đặt: ta được phương trình bậc hai theo t: 
	Vì nên (3) có nghiệm khi: 
	Giải (3), với mỗi nghiệm t0, ta có phương trình: 
	Ghi chú: 
	1/	Cách 2 thường dùng để giải và biện luận.
	2/	Cho dù cách 1 hay cách 2 thì điều kiện để phương trình có nghiệm: 
	3/	Bất đẳng thức B.C.S:
III. Phương trình thuần nhất bậc hai đối với sinx và cosx
Dạng: a sin2x + b sinx.cosx + c cos2x = d (1)
Cách giải: 
Cách 1:
·	Kiểm tra cosx = 0 có thoả mãn hay không?
	Lưu ý: cosx = 0 
·	Khi , chia hai vế phương trình (1) cho ta được: 
·	Đặt: t = tanx, đưa về phương trình bậc hai theo t:
Cách 2: Dùng công thức hạ bậc
	 (đây là phương trình bậc nhất đối với sin2x và 	cos2x)
IV. Phương trình đối xứng và nửa đối xứng đối với sinx và cosx
Dạng 1: a.(sinx ± cosx) + b.sinx.cosx + c = 0
·	Đặt: 
·	Thay vào phương trình đã cho, ta được phương trình bậc hai theo t. Giải phương trình này tìm t thỏa Suy ra x.
Lưu ý dấu:
·	
·	 
Dạng 2: a.|sinx ± cosx| + b.sinx.cosx + c = 0
·	Đặt: 
·	Tương tự dạng trên. Khi tìm x cần lưu ý phương trình chứa dấu giá trị tuyệt đối.
B. CÁC DẠNG BÀI TẬP:
Dạng 1: Phương trình bậc nhất và bậc hai với một hàm số lượng giác
Ví dụ 1: Giải các phương trình sau:
a) 	b) 
Ví dụ 2: Giải các phương trình sau:
	a) 	b) 
Ví dụ 3: Giải các phương trình:
	a) 	b) 
Ví dụ 4: Giải các phương trình 
	a) 	b) 
Dạng 2: Phương trình bậc nhất đối với sinx và cosx 
Ví dụ 1: Giải các phương trình sau:
	a) 	b) 
	c) 	d) 
Ví dụ 2: Giải phương trình
	a) 
	b) 
Dạng 3: Phương trình thuần nhất bậc hai đối với sinx và cosx
Ví dụ 1: Giải các phương trình sau:
	a) 	b) 
Ví dụ 2: Giải các phương trình sau:
	a) 	b) 
Ví dụ 3: Giải các phương trình sau:
	a) 	b) 
Ví dụ 4: Cho phương trình . Tìm m để phương trình có hai nghiệm với và 
Dạng 4: Một số dạng phương trình lượng giác khác
Ví dụ 1: Giải các phương trình sau:
	a) 	b) 
Ví dụ 2: Giải các phương trình 
	a) 	b) 
Dạng 5: Tìm điều kiện để phương trình lượng giác chứa tham số có nghiệm
Phương pháp: 
Ví dụ 1: Tìm giá trị của m để các phương trình sau đây có nghiệm
	a) 	b) 
Ví dụ 2: Tìm m để các phương trình sau có nghiệm
	a) 	b) 
C. BÀI TẬP LUYỆN TẬP
Phương trình bậc nhất và bậc hai đối với một hàm số lượng giác
Bài 1: Giải các phương trình:
	a) 	b) 
	c) 	d) 
Bài 2: Giải các phương trình
	a) 	b) 
	c) 	d) 
Bài 3: Giải các phương trình sau
	a) 	b) 
Bài 4: Giải các phương trình sau đây:
	a) 	b) 
Bài 5: Giải các phương trình sau đây
	a) 	b) 
Bài 6: Tìm m nguyên dương để phương trình có nghiệm.
Bài 7: Cho phương trình 
	a) Giải phương trình khi 	b) Tìm m để phương trình có nghiệm	
Phương trình bậc nhất đối với sinx và cosx
Bài 8: Giải các phương trình sau:
	a) 	b) 
	c) 	d) 
Bài 9: Giải các phương trình sau
	a) 	b) 
	c) 	d) 
Bài 10: tìm nghiệm của các phương trình sau đây thỏa mãn điều kiện chỉ ra
	a) với điều kiện 
	b) với điều kiện 
Bài 11: Giải các phương trình sau đây
	a) 	
	b) 
Bài 12: Tìm m để phương trình có nghiệm
Phương trình thuần nhất bậc hai đối với sinx và cosx
Bài 13: Giải các phương trình sau:
	a) 	b) 
	c) 	d) 
Bài 14: Giải phương trình 
Bài 15: Cho phương trình 
	a) Giải phương trình khi m=-2
	b) Tìm m để phương trình có nghiệm
Phương trình lượng giác sử dụng công thức biến đổi
Bài 16: Giải các phương trình sau:
	a) 	b) 
	c) 	d) 
Bài 17: Giải các phương trình sau
	a) 
	b) 
Bài 18: Giải các phương trình sau:
	a) 	b) 
Bài 19: Giải các phương trình sau
	a) 
	b) 
Phương trình lượng giác sử dụng công thức hạ bậc
Bài 20: Giải các phương trình sau
	a) 	b) 
Bài 21: Giải các phương trình sau đây
	a) 	b) 
	c) 	d) 
Một số dạng phương trình lượng giác khác
Bài 22: Giải các phương trình 
	a) 	b) 
Giải phương trình bằng cách đặt ẩn phụ hoặc đưa về phương trình tích
Bài 23: Giải các phương trình sau
	a) 	b) 
Bài 24: Giải các phương trình sau
	a) 	b) 
Phương trình lượng giác khác
Giải các phương trình sau:
	1) sin2x = sin23x	2) sin2x + sin22x + sin23x = 
	3) cos2x + cos22x + cos23x = 1	4) cos2x + cos22x + cos23x + cos24x = 
Giải các phương trình sau:
	1) sin6x + cos6x = 	2) sin8x + cos8x = 
	3) cos4x + 2sin6x = cos2x	4) sin4x + cos4x – cos2x + – 1 = 0
Giải các phương trình sau:
	1) 1 + 2sinx.cosx = sinx + 2cosx	2) sinx(sinx – cosx) – 1 = 0
	3) sin3x + cos3x = cos2x	4) sin2x = 1 + cosx + cos2x
	5) sinx(1 + cosx) = 1 + cosx + cos2x	6) (2sinx – 1)(2cos2x + 2sinx + 1) = 3 – 4cos2x
	7) (sinx – sin2x)(sinx + sin2x) = sin23x	
	8) sinx + sin2x + sin3x = (cosx + cos2x + cos3x)
Giải các phương trình sau:
	1) 2cosx.cos2x = 1 + cos2x + cos3x	2) 2sinx.cos2x + 1 + 2cos2x + sinx = 0
	3) 3cosx + cos2x – cos3x + 1 = 2sinx.sin2x
	4) cos5x.cosx = cos4x.cos2x + 3cos2x + 1
Giải các phương trình sau:
	1) sinx + sin3x + sin5x = 0	2) cos7x + sin8x = cos3x – sin2x
	3) cos2x – cos8x + cos6x = 1	4) sin7x + cos22x = sin22x + sinx
Giải các phương trình sau:
	1) sin3x + cos3x + = cosx + sin3x
	2) 1 + sin2x + 2cos3x(sinx + cosx) = 2sinx + 2cos3x + cos2x