Bài kiểm tra 45 phút môn Hình học lớp 8 - Tiết 25

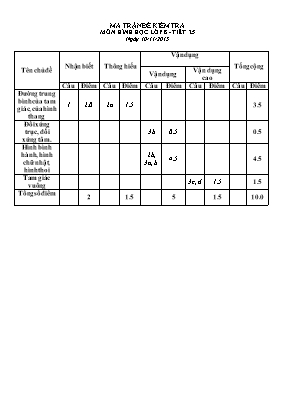
MA TRẬN ĐỀ KIỂM TRA
MễN HèNH HỌC LỚP 8 - TIẾT 25
Ngày 10/11/2015
Tờn chủ đề
Nhận biết
Thụng hiểu
Vận dụng
Tổng cộng
Vận dụng
Vận dụng
cao
Cõu
Điểm
Cõu
Điểm
Cõu
Điểm
Cõu
Điểm
Cõu
Điểm
Đường trung bỡnh của tam giỏc, của hỡnh thang
1
2.0
2a
1.5
3.5
Đối xứng trục, đối xứng tõm.
3b
0.5
0.5
Hỡnh bỡnh hành, hỡnh chữ nhật, hỡnh thoi
2b,
3a, b
4.5
4.5
Tam giỏc vuụng
3c, d
1.5
1.5
Tổng số điểm
2
1.5
5
1.5
10.0
TRƯỜNG THCS TRẦN PHÚ
Họ và tờn: ..................................................
Lớp: 8..
BÀI KIỂM TRA 45 PHÚT
MễN HèNH HỌC LỚP 8 - TIẾT 25
Ngày 10/11/2015 
Lời phờ của thầy, cố giỏo
Điểm
(Học sinh làm trực tiếp vào bài kiểm tra này)
Bài 1 ( 2.0 đ ) Tỡm x trờn hỡnh 
 Hỡnh 1
Bài 2( 3.0 đ )
Tứ giỏc ABCD cú hai đường chộo vuụng gúc với nhau. Gọi M, N, P, Q theo thứ tự là trung điểm của cỏc cạnh AB, BC, CD, DA. 
a) Tứ giỏc MNPQ là hỡnh gỡ ? Vỡ sao?
b) Hai đường chộo AC và BD cú thờm điều kiện gỡ thỡ tứ giỏc MNPQ là hỡnh vuụng?
Bài 3( 5.0 đ )
Cho tam giỏc ABC vuụng tại A, trung tuyến AM, đường cao AH. Từ M kẻ ME, MF lần lượt vuụng úc với AB, AC. Gọi I là điểm đối xứng của M qua F
a/ Chứng minh tứ giỏc AEMF là hỡnh chữ nhật.
b/Tứ giỏc AICM là hỡnh gỡ ? Vỡ sao ?
c/ Chứng minh HE vuụng gúc với HF ?
d/ AB2+AC2=IA2+IC2+2AM2 
Bài làm
...................................................................................................................................................
...................................................................................................................................................
................................................................................................................................................... ...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
ĐÁP ÁN VÀ BIỂU ĐIỂM 
BÀI
CÂU
NỘI DUNG
ĐIỂM
1
2,0đ
Ta cú: IK// AD // BC; ( vỡ cựng vuụng gúc với CD )
* Vỡ IA = IB ( Giả thiết )
IK // AD ( // BC ) ( chứng minh trờn )
Suy ra: KD = KC ; ( Định lý về đường trung bỡnh của hỡnh thang )
Mà KD = 10 dm.
Vậy: KC = 10 dm, hay x = 10 dm
Hỡnh vẽ đỳng
0,25 ủ
0,75đ
0, 5 ủ
0, 5 ủ
2
3,0 đ
a) Sử dụng tớnh chất đường trung bỡnh của tam giỏc, chứng minh được MNPQ là hỡnh bỡnh hành.
* Chứng minh được là hỡnh chữ nhật
b) Chứng minh được nếu hai đường chộo cú thờm điều kiện bằng nhau thỡ MNPQ là hỡnh vuụng 
Hỡnh vẽ 
0,5 ủ
1,0 ủ
1, ủ
0.5 ủ
3
0
a/Chứng minh được cú 3 gúc vuụng suy ra là hỡnh chữ nhật
Vẽ hỡnh đỳng 
0.5
1.5
b
Chứng minh được AC vuụng gúc với MI tại trung điểm mỗi đường Vậy Tứ giỏc AICM là hỡnh thoi
1.5
c
cm được HO =1/2AM => HO=1/2EF => Tam giỏc EHF vuụng tại H
HE vuụng HF
1
d
AB2+AC2= BC2=(BM+MC)2 =BM2+MC2+2.BM.MC 
Mà BM=MC=AM=IA=IC =>AB2+AC2 =IA2+IC2+2AM2 
0.5
DUYỆT CỦA CHUYấN MễN