2 Đề thi thử vào Lớp 10 THPT môn Toán - Năm học 2016-2017 - Trường THPT Đông Sơn I (Có đáp án)

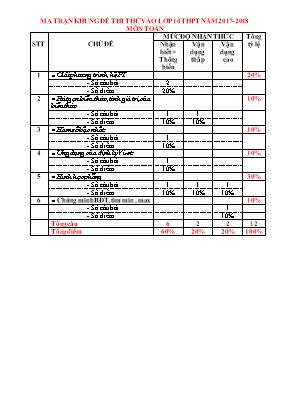
MA TRẬN KHUNG ĐỀ THI THỬ VÀO LỚP 10 THPT NĂM 2017- 2018
MÔN TOÁN 
STT
CHỦ ĐỀ
MỨC ĐỘ NHẬN THỨC
Tổng tỷ lệ
Nhận biết +
Thông hiểu
Vận dụng thấp
Vận dụng cao
1
 Giải phương trình, hệ PT
20%
 - Số câu hỏi
2
 - Số điểm
20%
2
 Rút gọn biểu thức, tính giá trị của biểu thức
10%
 - Số câu hỏi
1
1
 - Số điểm
10%
10%
3
 Hàm số bậc nhất
10%
 - Số câu hỏi
1
 - Số điểm
10%
4
 Ứng dụng của định lý Vi-et
10%
 - Số câu hỏi
1
 - Số điểm
10%
5
 Hình học phẳng
30%
 - Số câu hỏi 
1
1
1
 - Số điểm
10%
10%
10%
6
 Chứng minh BĐT, tìm min , max
10%
 - Số câu hỏi
1
 - Số điểm
10%
Tổng câu
6
2
2
12
Tổng điểm
60%
20%
20%
100%
SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT ĐÔNG SƠN I
ĐỀ A
ĐỀ THI THỦ VÀO LỚP 10 THPT 
NĂM HỌC 2016 – 2017
Môn: Toán 
(Thời gian làm bài 120 phút )
Ngày thi: 25/5/2016
Câu 1(2,0 điểm) 
1.Giải phương trình khi m = 1
2.Giải hệ phương trình 
Câu 2(2,0 điểm) Cho biểu thức P = với x > 0 và x ¹ 1
1.Rút gọn P
2.Tính giá trị của x khi P = 3
Câu 3(2,0 điểm)
1.Cho hàm số . Tìm m, n biết đồ thị hàm số song song với đường thẳng và đi qua điểm A(1; 2016)
2.Tìm n để phương trình x2 - 2(n - 1)x - n - 5 = 0 (1) có 2 nghiệm thoả mãn hệ thức = 14. 
Câu 4(3,0 điểm)
Cho đường tròn (O; R), đường kính AB vuông góc với dây cung MN tại điểm H (H nằm giữa O và B). Trên tia đối của tia NM lấy điểm C nằm ngoài đường tròn (O; R) sao cho đoạn thẳng AC cắt đường tròn (O; R) tại điểm K khác A. Hai dây MN và BK cắt nhau ở E. Qua N kẻ đường thẳng vuông góc với AC cắt tia MK tại F. 
1.Chứng minh tứ giác AHEK nội tiếp 
2.Chứng minh tam giác NFK cân và EM.NC=EN.CM
3.Giả sử KE =KC. Chứng minh OK // MN 
Câu 5(1,0 điểm)
Cho các số dương x, y, z thỏa mãn: x + y + z = 1.
Chứng minh rằng: + + 
 ...............................Hết......................................
Họ và tên thí sinh......................................................SBD.....................................
TRƯỜNG THPT ĐÔNG SƠN I 
HƯỚNG DẪN CHẤM TOÁN KÌ THI THỦ VÀO 10 THPT
Năm học 2017 - 2018
ĐỀ A
Câu
Nội dung
Điểm
1
2,00
1. Khi m = 1 ta có PT 
Phương trình đã cho có hai nghiệm x = -1 và x = -2
0,5
0,5
2. Ta có 
0,5
 Hệ có một nghiệm (x;y) = (3; 1)
Cách 2: Từ PT (1) ta có x = y+2 thế vào PT (2) ta được 5y = 5 . Hệ đã cho có một nghiệm (x;y) = (3; 1)
0,5
2.1
1,00
Ta có: P = 
0,25
= 
0,25
= 
0,25
= = = 
0,25
2.2
1.00
Với P = 3 ta có = 3 
0,25
=> 3x + - 2 = 0 
0,25
=> 
0,25
=> 
0,25
3.1
1,00
Từ giả thiết đồ thị hàm số song song với đường thẳng (d) ta có 
m = -1
0,25
Đồ thị hàm số đi qua A(1; 2016) nên 2016 = m + n
0,25
Ta có hệ 
0,25
Vậy m = -1; n = 2017
0,25
3.2
1,00
Phương trình bậc hai ẩn x có 2 nghiệm 
∆’ (n - 1)2 + (n + 5) ≥ 0 n2 – 2n + 1 + n + 5 ≥ 0 
n2 - n + 6 > 0 đúng .Chứng tỏ phương trình có 2 nghiệm phân biệt n
0,25
Theo hệ thức Vi ét ta có: 
0,25
Ta có = 14 (x1 + x2)2 - 2x1x2 = 14 4 (n - 1)2 + 2 (n + 5) = 14
0,25
 4n2 – 6n + 14 = 14 
Vậy n = 0 ; n =
0,25
4.1
1,00
0,25
Xét tứ giác AHEK có: 
0,25
(Góc nội tiếp chắn nửa đường tròn)
0,25
 Tứ giác AHEK nội tiếp 
0,25
4.2
1,00
Do đường kính AB MN nên B là điểm chính giữa cung MN (1)
Ta lại có: (cùng vuông góc với AC)
 (so le trong) (2)
 (đồng vị) (3)
0,25
Từ (1);(2);(3) hay 
 cân tại K
0,25
có KE là phân giác của góc 
0,25
Ta lại có:; KE là phân giác của góc là phân giác ngoài của tại K (5)
Từ (4) và (5) 
0,25
4.3
1,00
 Ta có vuông tại K
0,25
Theo giả thiết ta lại có vuông cân tại K
0,25
Ta có 
0,25
Mặt kháccân tại Ovuông cân tại O
 (cùng vuông góc với AB)
0,25
5
1,00
Ta có: 4( 2x2 + xy + 2y2 ) = 5(x+ y)2 + 3(x- y)2 5(x+ y)2 
Dấu ‘‘ =’’ xảy ra khi x = y
0,25
Vì x, y > 0 nên 2 . Dấu ‘‘=’’ xảy ra khi x = y
Chứng minh tương tự ta có: 
2 . Dấu ‘‘=’’ xảy ra khi y = z
2 . Dấu ‘‘=’’ xảy ra khi z = x
0,25
Cộng ba bất đẳng thức trên vế theo vế, ta được:
++
0,25
Do x+ y+ z = 1, suy ra: 
++. 
Dấu ‘‘=’’xảy ra khi x = y = z = 
0,25
Ghi chú : 
- Đối với câu 4: Nếu học sinh không có hình vẽ hoặc vẽ hình sai thì không chấm câu này
SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT ĐÔNG SƠN I
ĐỀ B
ĐỀ THI THỦ VÀO LỚP 10 THPT 
NĂM HỌC 2016 – 2017
Môn: Toán 
(Thời gian làm bài 120 phút )
Ngày thi: 25/5/2016
Câu 1(2,0 điểm) 
1.Giải phương trình khi n =1
2.Giải hệ phương trình 
Câu 2(2,0 điểm) 
Cho biểu thức Q = với y > 0 và y ¹ 1
1.Rút gọn Q
2.Tính giá trị của y khi Q = 3
Câu 3(2,0 điểm)
1.Cho hàm số . Tìm a, b biết đồ thị hàm số song song với đường thẳng và đi qua điểm B(1; 2016)
2.Tìm m để phương trình x2 - 2 (m - 1)x - m - 5 = 0 (1) có 2 nghiệm thoả mãn hệ thức = 14. 
Câu 4 (3,0 điểm)
 Cho đường tròn (O; R), đường kính AB vuông góc với dây cung MN tại điểm H (H nằm giữa O và B). Trên tia đối của tia NM lấy điểm C nằm ngoài đường tròn (O; R) sao cho đoạn thẳng AC cắt đường tròn (O; R) tại điểm K khác A. Hai dây MN và BK cắt nhau ở E. Qua N kẻ đường thẳng vuông góc với AC cắt tia MK tại F. 
1.Chứng minh tứ giác AHEK nội tiếp 
2.Chứng minh tam giác NFK cân và EM.NC = EN.CM
3.Giả sử KE =KC. Chứng minh OK // MN 
Câu 5(1,0 điểm)
Cho các số dương a, b, c thỏa mãn: a + b + c = 1.
Chứng minh rằng: 
 ...............................Hết......................................
Họ và tên thí sinh......................................................SBD..................................
TRƯỜNG THPT ĐÔNG SƠN I 
HƯỚNG DẪN CHẤM TOÁN KÌ THI THỦ VÀO 10 THPT
Năm học 2017 - 2018
ĐỀ B
Câu
Nội dung
Điểm
1
2,00
1. Khi n = 1 ta có PT 
Phương trình đã cho có hai nghiệm x = -1 và x = -2
0,5
0,5
2. Ta có 
0,5
 Hệ có một nghiệm (x;y) = (3; 1)
Cách 2: Từ PT (1) ta có y = 4-x thế vào PT (2) ta được 5x = 15 
. Hệ đã cho có một nghiệm (x;y) = (3; 1)
0,5
2.1
1,00
Ta có Q = 
0,25
= 
0,25
= 
0,25
= = = 
0,25
2.2
1.00
Với Q = 3 ta có = 3 
0,25
=> 3y + - 2 = 0 
0,25
=> ( Thỏa mãn) 
0,25
=> 
0,25
3
1,00
Từ giả thiết đồ thị hàm số song song với đường thẳng (d) ta có 
a = -1
0,25
Đồ thị hàm số đi qua B(1 ;2016) nên 2016 = a+b
0,25
Ta có hệ 
0,25
Vậy a = -1; b = 2017
0,25
4
1,00
Phương trình bậc hai ẩn x có 2 nghiệm 
∆’ (m - 1)2 + m + 5≥ 0 m2 - 2m + 1 + m + 5 ≥ 0 
m2 - m + 6 > 0 đúng . Chứng tỏ phương trình có 2 nghiệm phân biệt m
0,25
Theo hệ thức Vi ét ta có: 
0,25
Ta có = 14 (x1 + x2)2 - 2x1x2 = 14 4 (m - 1)2 + 2 (m + 5) = 14
0,25
 4m2 - 6m + 14 = 14 
Vậy m = 0; m = 
0,25
4.1
1,00
0,25
Xét tứ giác AHEK có: 
0,25
(Góc nội tiếp chắn nửa đường tròn)
0,25
 . Tứ giác AHEK nội tiếp 
0,25
4.2
1,00
Do đường kính AB MN nên B là điểm chính giữa cung MN (1)
Ta lại có: (cùng vuông góc với AC)
 (so le trong) (2)
 (đồng vị) (3)
0,25
Từ (1);(2);(3) hay 
 cân tại K
0,25
có KE là phân giác của góc 
0,25
Ta lại có:; KE là phân giác của góc là phân giác ngoài của tại K (5)
Từ (4) và (5) 
0,25
4.3
1,00
 Ta có vuông tại K
0,25
Theo giả thiết ta lại có vuông cân tại K
0,25
Ta có 
0,25
Mặt kháccân tại Ovuông cân tại O
 (cùng vuông góc với AB)
0,25
5
1,00
Ta có: 4( 2a2 + ab + 2b2 ) = 5(a+ b)2 + 3(a- b)2 5(a+ b)2 
Dấu ‘‘ =’’ xảy ra khi a = b
0,25
Vì a, b > 0 nên . Dấu ‘‘=’’ xảy ra khi a = b
Chứng minh tương tự ta có: 
. Dấu ‘‘=’’ xảy ra khi b = c
. Dấu ‘‘=’’ xảy ra khi c = a
0,25
Cộng ba bất đẳng thức trên vế theo vế, ta được:
0,25
Do a + b + c = 1, suy ra: 
Dấu ‘‘=’’xảy ra khi a = b =c = 
0,25
Ghi chú : 
- Đối với câu 4: Nếu học sinh không có hình vẽ hoặc vẽ hình sai thì không chấm câu này