Trắc nghiệm Toán 12 - Học kì I - Năm học 2016-2017

Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 1 
Câu 1 : Cho hàm số y = f(x) có ( ) và ( ) . Khẳng định nào 
sau đây là khẳng định đúng ? 
A. Đồ thị hàm số đã ho ó hai ti m cận ngang là đường thẳng y = 1 và y = -1. 
B. Đồ thị hàm số đã ho không ó ti m cận ngang. 
C. Đồ thị hàm số đã ho ó đúng một ti m cận ngang. 
D. Đồ thị hàm số đã ho ó hai ti m cận ngang là đường thẳng x = 1 và x = -1. 
Câu 2 : Giá trị nhỏ nhất của hàm số là 
A. 0 B. -1 C. 5 D. -5 
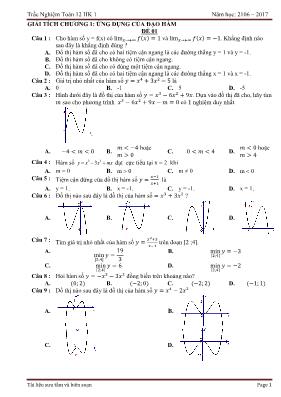
Câu 3 : Hình dưới đây là đồ thị của hàm số . Dựa vào đồ thị đã ho, hãy tìm 
 sao ho phương trình có nghi m duy nhất 
A. B. 
 hoặc 
C. D. 
 hoặc 
Câu 4 : Hàm số 3 23y x x mx   đạt cực tiểu tại x = 2 khi 
A. m = 0 B. m  0 C. m ≠ 0 D. m  0 
Câu 5 : Ti m cận đứng của đồ thị hàm số 
 là 
A. y = 1. B. x = -1. C. y = -1. D. x = 1. 
Câu 6 : Đồ thị nào sau đây là đồ thị của hàm số ? 
A. 
B. 
C. 
D. 
Câu 7 : Tìm giá trị nhỏ nhất của hàm số 
 trên đoạn [2 ;4]. 
A. 
B. 
C. 
 D. 
Câu 8 : Hỏi hàm số đồng biến trên khoảng nào? 
A. ( ) B. ( ) C. ( ) D. ( ) 
Câu 9 : Đồ thị nào sau đây là đồ thị của hàm số 
A. 
B. 
C. 
D. 
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 2 
Câu 10 : Hàm số nào sau đây đồng biến trên các khoảng x định của nó? 
A. 
 . B. 
 . 
C. 
 . D. 
 . 
Câu 11 : Hỏi hàm số 
 nghịch biến trên các khoảng nào ? 
A. ( ) và ( ) B. ( ) và ( ) 
C. ( ) và ( ) D. ( ) và ( ) 
Câu 12 : Giá trị cực tiểu yCT của hàm số 
 bằng 
A. 
 B. 
 C. 0 D. 
Câu 13 : Giá trị cực đại yCĐ của hàm số y = x
3
 – 3x + 2 là 
A. 0. B. 4. C. 1. D. -1. 
Câu 14 : Cho các hàm số (1): ; (2): ; (3): 
; (4): 
. Trong 
các hàm số trên, những hàm số nào không có cực trị? 
A. (2) và (4) B. (1) và (2) C. (3) và (4) D. (1) và (3) 
Câu 15 : Cho hàm số y = f(x) x định và liên tục trên R và có bảng biến thiên dưới đây. Khẳng 
định nào sau đây là khẳng định đúng ? 
x 1 0 1   
y’ 0 0 0    
y  3  
A. Hàm số đạt cự đại tại x = 0 và đạt cực 
tiểu tại x = ± 1. 
B. Hàm số có giá trị lớn nhất bằng -3 
C. Hàm số ó đúng một cực trị. D. Hàm số có ba cực trị. 
Câu 16 : Giá trị lớn nhất của hàm số 
 trên đoạn [-2;0] là 
A. 
 B. 4 C. 
 D. -4 
Câu 17 : Ti m cận ngang của đồ thị hàm số 
 là 
A. y = 0. B. x = 1. C. x = -1. D. y = 2. 
Câu 18 : Phương trình tiếp tuyến của đồ thị hàm số y = x
3
 – 3x2 + 1 tại điểm ó hoành độ bằng 2 
là : 
A. y = -2 B. y = 3 C. y = 2 D. y = -3 
Câu 19 : 
H số góc của tiếp tuyến của đồ thị hàm số 
1
1
x
y
x



tại điểm giao điểm của đồ thị hàm 
số với trục tung bằng: 
A. -2 B. 1 C. -1 D. 2 
Câu 20 : Biết rằng đường thẳng y = -2x + 2 c t đồ thị hàm số y = x
3
 + x + 2 tại điểm duy nhất ; 
kí hi u (x0 ;y0) là t a độ của điểm đó. Tìm y0. 
A. y0 = 4. B. y0 = 2. C. y0 = 0. D. y0 = -1. 
 --- --- 
-4 -4 
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 3 
Câu 1. Đồ thị hàm số nào sau đây ó dạng như hình vẽ: 
A. 4 22y x x  B. 4 22 1y x x   C. 4 22y x x  D. 4 22y x x   
Câu 2. Cho hàm số 3
2
y
x


.Số ti m cận của đồ thị hàm số bằng: 
A. 2 B. 1 C. 0 D. 3 
Câu 3. Có bao nhiêu tiếp tuyến với đồ thị hàm số 
2 3
2 1
x
y
x



 biết tiếp tuyến vuông góc với đường 
thẳng 
1
2
y x 
A. 3 B. 1 C. 0 D. 2 
Câu 4. Điểm cực tiểu của hàm số : 3 3 4y x x    là x = 
A. -1 B. 1 C. - 3 D. 3 
Câu 5. Đồ thị hàm số nào sau đây ó dạng như hình vẽ: 
A. 3 22y x x   B. 3 2y x x  C. 3 22 1y x x   D. 3 22y x x  
Câu 6. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 5 4y x  trên đoạn  1;1 là: 
A. 1; 3M m    ; B. 9; 1M m  ; C. 1; 1.M m   D. 3; 1M m  ; 
Câu 7. Đồ thi hàm số 3 3 1y x x   ó điểm cực tiểu là: 
A. ( 1 ; 3 ) B. ( -1 ; 3 ) C. ( -1 ; 1 ) D. ( 1 ; -1 ) 
Câu 8. Giá trị của tham số m để phương trình 3 3 2 2x x m     ó 3 nghi m phân i t. 
A. 4 0m   B. 0 4m  C. 0 2m  D. 2 0m   
Câu 9. Hàm số 3 1y x mx   có 2 cực trị khi : 
A. 0m  B. 0m  C. 0m  D. 0m  
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 4 
Câu 10. Giá trị nhỏ nhất của hàm số hàm số 
1
2
y x
x
 

 trên  1;2 là 
A. 
9
4
 B. 
1
2
 C. 0 D. 2 
Câu 11. Hàm số : 3 23 4y x x   nghịch biến trên khoảng: 
A. ( 3;0) B. (0; ) C. ( 2;0) D. ( ; 2)  
Câu 12. Với giá trị nào của m thì hàm số 
1 3 2
2 2
3
y x x mx     nghịch biến trên tập x định 
của nó? 
A. 4m  B. 4m  C. 4m  D. 4m  
Câu 13. Đồ thị hàm số nào sau đây ó dạng như hình vẽ: 
A. 
1
x
y
x


 B. 
1
x
y
x



 C. 
1
x
y
x


 D. 
1x
y
x

 
Câu 14. H số góc của tiếp tuyến của đồ thị hàm số 1
1
x
y
x



tại điểm giao điểm của đồ thị hàm số 
với trục tung bằng: 
A. -1 B. 2 C. -2 D. 1 
Câu 15. Số giao điểm của đường thẳng 2y x  và đường cong 
2 2016
2
x
y
x



 là: 
A. 3 B. 0 C. 2 D. 1 
Câu 16. Đường thẳng y = m c t đồ thị hàm số 3 3 2y x x   tại 3 điểm phân bi t khi: 
A. 0 4m  B. 4m  C. 0 4m  D. 0 4m  
Câu 17. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 3 23 9 35y x x x    trên đoạn  4;4 
là: 
A. 40; 8.M m   B. 40; 8M m  ; C. 40; 41M m   ; D. 15; 41M m   ; 
Câu 18. Điểm cự đại của hàm số : 4 21 2 3
2
y x x   là x = 
A. 2 B. 2 C. 2 D. 0 
Câu 19. Kết luận nào sau đây về tính đơn đi u của hàm số 2 1
1



x
y
x
 là đúng? 
A. Hàm số luôn luôn đồng biến trên  1\ ; 
B. Hàm số đồng biến trên các khoảng (–; –1) và (–1; +). 
C. Hàm số nghịch biến trên các khoảng (–; –1) và (–1; +); 
D. Hàm số luôn luôn nghịch biến trên  1\ ; 
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 5 
Câu 20. Số giao điểm của đường thẳng 1y x  và đường cong 
2 4
1
x
y
x



 là: 
A. 2 B. 3 C. 0 D. 1 
Câu 21. Giá trị của tham số m để hàm số : 3 2 2( 1) 1y x m x m x     đạt cự đại tại x= -1 là: 
A. m = -2 B. Không có giá trị m C. m= -1 D. 1m   
Câu 22. Giá trị của tham số m để phương trình 4 22 0x x m   ó 4 nghi m phân i t. 
A. 
1
0
m
m
 
 
 B. 0 1m  C. 1 0m   D. 1 1m   
Câu 23. Cho hàm số y = –x3 + 3x2 – 3x + 1, m nh đề nào sau đây là đúng? 
A. Hàm số luôn luôn đồng biến trên khoảng x định; 
B. Hàm số luôn luôn nghịch biến trên khoảng x định; 
C. Hàm số đạt cự đại tại x = 1; 
D. Hàm số đạt cực tiểu tại x = 1. 
Câu 24. Cho hàm số 3 1
2 1
x
y
x



.Khẳng định nào sau đây đúng? 
A. Đồ thị hàm số có ti m cận ngang là 3
2
y  B. Đồ thị hàm số không có ti m cận. 
C. Đồ thị hàm số có ti m cận đứng là x= 1 D. Đồ thị hàm số có ti m cận đứng là 3
2
y  
Câu 25. Hàm số : 4 22 4y x x   nghịch biến trên khoảng: 
A. ( 1;0) (1; )   B. ( ; 1)  và (0;1) C. ( 1;0) và (1; ) D. ( ; 1) (0;1)   
Câu 26. Cho hàm số 
2
3
3 2
x
y
x x


 
.Số ti m cận của đồ thị hàm số bằng: 
A. 1 B. 0 C. 3 D. 2 
Câu 27. Khẳng định nào sau đây là đúng về đồ thị hàm số 
2 2 5
1
x x
y
x
  


 : 
A. 1CDx   B. 0CD CTy y  C. 4CTy   D. 3CD CTx x  
Câu 28. Giá trị của tham số m để phương trình 3 23 2 1x x m    ó 3 nghi m phân i t. 
A. 0 3m  B. 2 0m   C. 3 1m   D. 2 4m  
Câu 29. Giá trị của tham số m để hàm số : 3 23 2 1y x x mx    đạt cự đại tại x =2 là: 
A. m = 0 B. Không có giá trị m. 
C. m= 2 D. 0m  
Câu 30. Cho hàm số 
1
2 1
x
y
x



. Ch n phương n đúng trong phương n sau: 
A. 
 1;0
max 0y

 B. 
 3;5
11
min
4
y  C. 
 1;2
1
min
2
y

 D. 
 1;1
1
max
2
y

 
--- --- 
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 6 
Câu 1: Hàm số  3 2 2
1
1 2
3
y x mx m m x      đồng biến trên khi 
A. 1m   B. 1m   C. 1m   D. 1m   
Câu 2: Bảng biến thiên sau đây là ủa hàm số nào. 
x  1 1  
'y
  0  0  
y 
 4 
 0 
  
A. 3 3 2y x x   B. 3 3 1y x x    C. 3 3 2y x x    D. 3 3y x x   
Câu 3: Đường thẳng y m c t đồ thị hàm số 3 3y x x  tại duy nhất một điểm khi 
A. 2; 2m m   B. 2m   C. 2m  D. 2 2m   
Câu 4: Hàm số 4 22 1y x x    đạt GTLN  0;2 tại điểm ó hoành độ 
A. 1x  B. 0x  C. 1x   D. 2x  
Câu 5: Hàm số 
2 3
1
x
y
x



 nghịch biến trên 
A. B.  ; 1  C.    ; 1 ; 1;    D.  1;  
Câu 6: Hàm số 3 3 1y x x    đạt cự đại tại 
A. 1x  B. 2x  C. 1x   D. 0x  
Câu 7: Đồ thị hàm số 3 23 1y x x   có tiếp tuyến tại điểm ó hoành độ bằng 0 ó phương trình là 
A. 1y   B. 3 1y x   C. 1y x  D. 1y  
Câu 8: Bảng biến thiên sau đây là ủa hàm số nào. 
x  3 0 3  
'y  0  0  0  
y 
 
5
2
  
 2 2 
A. 4 2
1 5
3
2 2
y x x   B. 4 2
1
2
4
y x x   C. 4 2
1 5
2
2 2
y x x   D. 4 2
1 3
3
4 2
y x x   
Câu 9: Đường thẳng y x m  c t đồ thị 
1
x
y
x


 tại hai điểm phân bi t khi 
A. 2 2m   B. 2m   C. 2m  D. với m i m 
Câu 10: Baát phöông trình  2 1 4x m x m     coù nghieäm khi 
A. 1m   B. 2m  C. 0m  D. 2m  
Câu 11: Đồ thị sau đây là ủa hàm số nào? 
2
-2
-4
5
1
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 7 
A. 3 3y x x  B. 3 3y x x  C. 3 2y x x   D. 3 2y x x   
Câu 12: Đường thẳng 1y m  c t đồ thị 4 22 1y x x    tại 4 điểm phân bi t khi 
A. 1; 2m m  B. 1 2m  C. 2; 3m m  D. 2 3m  
Câu 13: Hàm số 3 3 2y x x   đồng biến trong khoảng 
A.  1;  B.  1;1 C.    ; 1 ; 1;   D.  ;1 
Câu 14: Đồ thị hàm số 4 22 2y x x   có tiếp tuyến tại điểm ó hoành độ bằng 2 ó phương trình 
là 
A. 24 38y x  B. 2y  C. 0y  D. 24 38y x   
Câu 15: GTLN, GTNN của hàm số 2 24 2 4 2016y x x x x     trên đoạn  0;4 lần lượt là 
A. 2016;2018 B. 2014;2024 C. 2016;2024 D. 2018;2024 
Câu 16: Hàm số 4 2
1
2
4
y x x  đạt GTCĐ tại điểm ó hoành độ 
A. 2x  B. 2x   C. 2x   D. 0x  
Câu 17: Đồ thị hàm số  4 22 2 1y x m x     c t trục hoành tại 4 điểm phân bi t khi 
A. 1; 2m m  B. 1m C. 1; 3m m  D. 3m  
Câu 18: Bảng biến thiên sau đây là ủa hàm số nào 
 x  - 1  
 y’ + + 
 y  2 
 2  
A. 
1
12



x
x
y B. 
x
x
y



1
2
 C. 
1
12



x
x
y D. 
12
1



x
x
y 
Câu 19: Hàm số  4 22 1 1y x m x m     có ba cực trị phân bi t khi 
A. 1m B. 1m   C. 1m  D. 1m   
Câu 20: Hàm số 
4
2
x
y
x



 đạt GTLN trên đoạn  0;1 là 
A. 3 B. 2 C. 5 D. 2 
Câu 21: Đồ thị sau đây là ủa hàm số nào 
A. 
2
1
x
y
x
 


 B. 
2 1
2 1
x
y
x
 


 C. 
1
x
y
x



 D. 
1
1
x
y
x
 


Câu 22: Đồ thị hàm số   21 2 2y x x mx m     c t trục hoành tại 3 diểm phân bi t khi 
A. 3 1; 2m m     B. 2m  C. 1; 2m m   D. 1m   
Câu 23: Đồ thị sau đây là ủa hàm số nào? 
4
2
-2
-4
-6
-5 5
1
2
-2
1
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 8 
A. 4 23 1y x x   B. 4 22 1y x x    C. 4 23 1y x x    D. 4 22 1y x x   
Câu 24: Hàm số 3 3y x x  ó GTLN và GTNN trên đoạn  0;2 lần lượt bằng 
A. 0;2 B. 2;4 C. 0;4 D. 2;2 
Câu 25: Hàm số 4 22 1y x x   đồng biến trong khoảng 
A.  1;  B.    1;0 ; 1;  C.    ; 1 ; 0;1  D.  ;1 
--- --- 
Câu 1: Biết rằng đường thẳng 2 2y x c t đồ thị hàm số 3 2y xx tại điểm duy nhất; kí 
hi u 0 0;x y là t a độ điểm đó. Tìm 0.y 
A. 0 4y . B. 0 2y . C. 0 0y . D. 0 1y . 
Câu 2: Giả sử hàm số f x ó đạo hàm trên khoảng ; .a b Khẳng định nào sau đây là khẳng định 
sai ? 
A. Nếu ' 0, ;f x a bx và hàm số f liên tục trên ;a b thì hàm số f đồng biến trên khoảng 
; .a b 
B. Nếu ' 0, ;f x ax b thì hàm số f đồng biến trên khoảng ; .a b 
C. Nếu ' 0, ;f x a bx thì hàm số f đồng biến trên khoảng ; .a b 
D. Nếu ' 0, ;f x a bx thì hàm số f không đổi trên khoảng ; .a b 
Câu 3: Giá trị lớn nhất của hàm số 3 22 3 12 2y x x x trên đoạn 1;2 là 
A. 6 . B. 10 . C. 11 . D. 15 . 
Câu 4: Số điểm cực trị của hàm số 3
1
7
3
y x x là 
A. 3. B. 1. C. 2. D. 0. 
Câu 5: Đồ thị hàm số nào dưới đây ó hình dạng như hình vẽ. 
A. 2 1y xx . B. 4 2 1y x x . C. 3 3 1y xx . D. 3 13y x x . 
Câu 6: Số nghi m nhiều nhất của phương trình 4 24 3x x m   có thể có là: 
A. 8; B. 6; C. 4; D. 10; 
Câu 7: Bất phương trình 1 5x x m    có nghi m khi và chỉ khi: 
A. 6;m  B. 6;m  C. 2 3;m  D. 6 2 3m  
Câu 8: Khoảng cách giữa hai đường ti m cận ngang của đồ thị hàm số 
2
2
2 1
2 4 2 4
x x x
y
x x x
  

   
 là: 
A. 2; B. 1; C. 4; D. 3; 
Câu 9: Giá trị lớn nhất của hàm số 2 2 3f x x x là 
A. 3 . B. 2 . C. 2 . D. 0 . 
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 9 
Câu 10: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 
tan 2
tan
x
y
x m
 đồng biến trên 
khoảng 0; .
4
A. 0m hoặc 1 2m B. 2m C. 1 2m . D. 0m . 
Câu 11: Số giao điểm của hai đường cong 3 2 2 3y x x x và 2 1y x x là 
A. 2 . B. 3 . C. 0 . D. 1 . 
Câu 12: Cho hàm số y f x có lim 1
x
f x và lim 1
x
f x . Khẳng định nào sau đây là khẳng 
định đúng ? 
A. Đồ thị hàm số đã ho không ó ti m cận ngang. B. Đồ thị hàm số đã ho ó đúng một ti m cận 
ngang. 
C. Đồ thị hàm số đã ho ó hai ti m cận ngang là đường thẳng 1y và 1y . 
D. Đồ thị hàm số đã ho ó hai ti m cận ngang là đường thẳng 1x và 1x . 
Câu 13: Giá trị nhỏ nhất của hàm số 3sin 4cosy x x là: A. 4 . B. 3 . C. 5 . D. 3 . 
Câu 14: Số đường ti m cận của đồ thị hàm số 
1
1
x
y
x
 là: A. 3. B. 2. C. 0. D. 1. 
Câu 15: Đồ thị của hàm số 
1
1
y x
x
A. C t đường thẳng 1y tại hai điểm. B. C t đường thẳng 4y tại hai điểm. 
C. Tiếp xúc với đường thẳng 0y . D. Không c t đường thẳng 2y . 
Câu 16: Hàm số 
2 5
3
x
y
x
 đồng biến trên: A. 3; . B. . C. \ 3 . D. ;3 . 
Câu 17: Trong các bất đẳng thức sau, bất đẳng thức nào là sai ? 
A. 
3
sin , 0.
6
x
x x x .B. 
2
cos 1 , 0.
2
x
x x C. 
3
sin , 0.
6
x
x x x D. 
2
cos 1 , 0.
2
x
x x 
Câu 18: Tìm tất cả các giá trị thực của tham số m sao ho đồ thị của hàm số 4 22 1y x mx có 
 a điểm cực trị tạo thành một tam giác vuông cân: A. 
3
1
9
m . B. 
3
1
9
m . C. 1m . D. 
1m . 
Câu 19: Hàm số 3 23 9 11f x x x x 
A. Nhận điểm 1x làm điểm cực tiểu. B. Nhận điểm 1x làm điểm cự đại. 
C. Nhận điểm 3x làm điểm cực tiểu. D. Nhận điểm 3x làm điểm cự đại. 
Câu 20: Tìm giá trị nhỏ nhất của hàm số 
2 3
1
x
y
x
 trên đoạn 2;4 . 
A. 
2;4
19
min
3
y . B. 
2;4
min 2y . C. 
2;4
min 3y . D. 
2;4
min 6y . 
Câu 21: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số 3 2
1
2 3 5
3
y x x x 
A. Song song với trục hoành. B. Song song với đường thẳng 1x . 
C. Có h số gó dương. D. Có h số góc bằng 1 . 
Câu 22: C đồ thị của hai hàm số 
1
3y
x
 và 24y x tiếp xúc với nhau tại điểm M ó hoành độ 
là 
A. 1x . B. 1x . C. 
1
2
x . D. 2x . 
Câu 23: Phương trình 22 3 1x x x x      có số nghi m là: A. 2; B. 3; C. 1; D. 4; 
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 10 
Câu 24: Đồ thị hàm số 3 3y x x c t 
A. Đường thẳng 4y tại hai điểm. B. Đường thẳng 
5
3
y tại a điểm. 
C. Trục hoành tại một điểm. D. Đường thẳng 3y tại hai điểm. 
Câu 25: Xét phương trình 3 23 .x x m 
A. Với 5,m phương trình đã ho ó a nghi m. 
B. Với 1,m phương trình đã ho ó hai nghi m 
C. Với 4,m phương trình đã ho ó a nghi m phân bi t. 
D. Với 2,m phương trình đã ho ó a nghi m phân bi t. 
--- --- 
Câu 1: Cho hàm số y = f(x) = ax3 + bx2 + cx + d , a 0 . Khẳng định nào sau đây sai? 
A.Đồ thị hàm số luôn c t trục hoành B.Hàm số luôn có cực trị 
C. lim ( )
x
f x

  D.Đồ thị hàm số luôn ó tâm đối xứng. 
Câu 2: Bảng biến thiên sau đây là ủa hàm số nào? 
A. xxxy 33 23  B. xxxy 33 23  C. xxxy 33 23  D. xxxy 33 23  
Câu 3: Cho hàm số 
3
2
y
x


. Số đường ti m cận của đồ thị hàm số bằng 
A.0 B.1 C.2 D.3 
Câu 4: Đường thẳng x = 1 là ti m cận đứng của đồ thị hàm số nào sao đây? 
A. 
x
x
y



1
1
 B. 
2
22



x
x
y C. 
x
x
y



1
1 2
 D. 
x
xx
y



2
232 2
Câu 5: Đồ thị hàm số nào sau đây ó 3 điểm cực trị : 
A. 4 22 1y x x   B. 4 22 1y x x   C. 4 22 4 1y x x   D. 4 22 1y x x    
Câu 6: Cho hàm số 
2
1



x
x
y . Trong các m nh đề sau, m nh đề nào sai. 
A. Đồ thị hàm số trên có ti m cận đứng x = 2. B. Đồ thị hàm số trên có ti m cận ngang y = 1 
C. Tâm đối xứng là điểm I(2 ; 1) D. C âu A, B, C đều sai. 
Câu 7: Hàm số 133  xxy ó đồ thị như hình vẽ. Khẳng định nào đúng? 
A. Đồ thị hàm số ó điểm cự đại là (1;-1) B. yCĐ = -3yCT 
C. Hàm số ó điểm cự đại là 3 D. Cả A, B, C đều sai. 
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 11 
Câu 8: Đồ thị sau đây là ủa hàm số nào ? 
A. 
1
12



x
x
y B. 
x
x
y



1
2
 C. 
1
1



x
x
y D. 
1
2



x
x
y 
Câu 9: Cho hàm số 133 23  xxxy . M nh đề nào sau đây là đúng? 
A. Hàm số luôn nghịch biến. B. Hàm số luôn đồng biến. 
C. Hàm số đạt cự đại tại x = 1. C. Hàm số đạt cực tiểu tại x = 1 . 
Câu 10: Cho hàm số 3 23 1y x x   . Tích các giá trị cự đại và giá trị cực tiểu của hàm số bằng 
A.-6 B.-3 C.0 D.3 
Câu 11. Kết luận nào sau đây về tính đơn đi u của hàm số 
2
1
x
y
x


 là đúng? 
A. Hàm số luôn nghịch biến trên R. B. Hàm số đồng biến trên các khoảng 
    ;11; và 
C. Hàm số luôn đồng biến trên }1{\ R D. Hàm số nghịch biến trên các khoảng 
    ;11; và 
Câu 12. Trong các hàm số sau, hàm số nào sau đây đồng biến trên khoảng (1 ; 3) ? 
A. 
1
3



x
x
y B. 
2
842



x
xx
y C. 422 xxy  D. 542  xxy 
Câu 13: Trên nửa khoảng ]3;0( . Kết luận nào đúng ho hàm số 
x
xy
1
 . 
A. Có giá trị lớn nhất và giá trị nhỏ nhất. B. Có giá trị nhỏ nhất và không có giá trị lớn 
nhất. 
C. Có giá trị lớn nhất và không có giá trị nhỏ nhất. D. Không có giá trị lớn nhất và giá trị nhỏ 
nhất. 
Câu 14: Giá trị lớn nhất của hàm số 
2

x
x
y trên nửa khoảng ( -2; 4 ] bằng. 
A. 
5
1
 B. 
3
1
 C. 
3
2
 D. 
3
4
Câu 15: Cho hàm số  3 2
1
2 1 1
3
y x m x m x     . M nh đề nào sau đây là sai? 
A. 1m  thì hàm số có cự đại và cực tiểu; B. 1m  thì hàm số ó hai điểm cực trị; 
C. 1m  thì hàm số có cực trị; D. Hàm số luôn luôn có cự đại và cực tiểu. 
Câu 16: Giá trị lớn nhất của hàm số xy 45 trên đoạn [-1 ; 1 ] bằng. 
A. 9 B. 3 C. 1 D. 0 
Câu 17. Số giao điểm của đường cong 12 23  xxxy và đường thẳng y = 1 – 2x là: 
A. 1 B. 2 C. 3 D. 0 
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 12 
Câu 18. G i M và N là giao điểm của đường cong 
2
67



x
x
y và đường thẳng y = x + 2 . Khi đó 
hoành độ trung điểm I của đoạn MN bằng: 
A. 7 B. 3 C. 
2
7
 D. 
2
7
Câu 19. Cho đường cong 133 23  xxxy ó đồ thị (C). Phương trình tiếp tuyến của (C) tại 
giao điểm của (C) với trục tung là: 
A. 18  xy B. 13  xy C. 18  xy D. 13  xy 
Câu 20: Cho hàm số y = x2-4x+3 ó đồ thị (P) .Nếu tiếp tuyến tại điểm M của (P) có h số góc 
bằng 8 thì hoành độ điểm M là 
A.12 B.6 C.-1 D.5 
Câu 21: Đồ thị sau đây là ủa hàm số 24 4xxy  . Với giá trị nào của m thì phương trình 
024 24  mxx có bốn nghi m phân bi t. ? 
A. 40  m B. 62  m C. 40  m D. 60  m 
Câu 22: Giá trị của m để hàm số 4 22 1y x mx   ó a điểm cực trị là. 
A. 0m B. 0m C. 0m D. 0m 
Câu 23. Giá trị của m để đường cong ))(1( 2 mxxxy  c t trục hoành tại a điểm phân bi t là: 
A. 2m  B. 
1
4
m  C. 
1
( ; ) \ { 2}
4
m   D. Đ p số khác 
Câu 24: Tìm tất cả các giá trị của m để hàm số mmxmxxy  23
3
1
 đồng biến trên R. 
A. 0m  hoặc 1m   B. 1m   C. Đ p số khác D. 0m  hoặc 1m   
Câu 25: Giá trị lớn nhất của hàm số xxy cos2 trên đoạn 





2
;0

 bằng. 
A. 2 B. 3 C. 1
4


 D. 
2

--- --- 
Tr Nghi m To n 12 HK 1 N m h : 2106 – 2017 
 s Page 13 
 – – 
C©u1: TÝnh: K = 
4
0,75
31 1
16 8
 
   
   
   
, ta ®-îc: 
 A. 12 B. 16 C. 18 D. 24 
C©u2: TÝnh: K = 
 
3 1 3 4
03 2
2 .2 5 .5
10 :10 0,25
 
 


, ta ®-îc 
 A. 10 B. -10 C. 12 D. 15 
C©u3: TÝnh: K = 
 
 
3
3
2 2
3
03 2
1
2 : 4 3
9
1
5 .25 0,7 .
2

 


 
  
 
 
  