Toán học - Diện tích hình phẳng

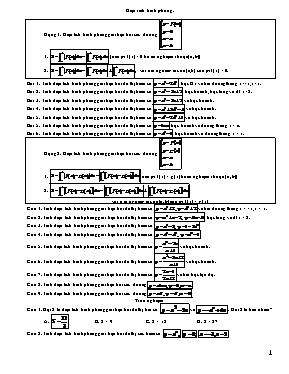
Diện tích hình phẳng.
Dạng 1: Diện tích hình phẳng giới hạn bởi các đường: 
1. (nếu pt f(x) = 0 ko có nghiệm thuộc (a;b)) 
2. , với c là nghiệm thuộc [a;b] của pt f(x) = 0.
Bài 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục Ox và hai đường thẳng x=-1, x=1. 
Bài 2: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành, trục tung và đt x=2.
Bài 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.
Bài 4: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.
Bài 5: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.
Bài 5: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và đường thẳng x = e.
Bài 6: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và đường thẳng x = 1.
Dạng 2: Diện tích hình phẳng giới hạn bởi các đường: 
1. (nếu pt f(x) = g(x) ko có nghiệm thuộc (a;b))
2. 
với c là nghiệm thuộc [a;b] của pt f(x) = g(x)
Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và hai đường thẳng x = -1, x = 1. 
Câu 2: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục tung và đt x = 2.
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số .
Câu 4: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số .
Câu 5. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.
Câu 6. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành. 
Câu 7. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và hai trục tọa độ. 
Câu 8. Tính diện tích hình phẳng giới hạn bởi các đường 
Câu 9. Tính diện tích hình phẳng giới hạn bởi các đường 
Trắc nghiệm
Câu 1: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hai số : và . Hỏi S là bao nhiêu?
A. 	B. S = 9	C. S = 12	D. S = 27
Câu 2: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số .
A. 	B. 	C. 	D. 
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số 
A. 	B. 	C. 	D. 
Câu 4: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và các hệ trục tọa độ.
A. 	B. 	C. 	D. 
Câu 5: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục tung. 
A. 	B. 	C. 	D. 
Câu 6: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 
A. 	B. 	C. 	D. 
Câu 7: Tính diện tích hình thang cong giới hạn bởi , trục hoành và hai đường thẳng 
A. 	B. 	C. 	D. 
Câu 8: Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số và 
A. 	B. 	C. 	D. 
Câu 9: Cho hàm số . Gọi S là diện tích hình phẳng gới hạn bởi đồ thị hàm số và trục hoành. Phát biểu nào sau đây là đúng ?
A. 	B. 	
C. 	D. 
Câu 10: Gọi S là diện tích hình thang cong giới hạn bởi đồ thị hàm số , trục hoành và đường thẳng . Tìm a để 
A. a = 2	B. 	C. a = 1	D. a = 4
Câu 11: Tìm a và b để diện tích hình thang cong giới hạn bởi , với bằng 
A. 	B. 	C. 	D. 
Câu 12: Tính diện tích hình phẳng giới hạn bởi .
A. 	B. 	C. 	D. 
Câu 13: Tính diện tích hình thang cong giới hạn bởi và 
A. 	B. 	C. 	D. 
Câu 14: Tính diện tích hình phẳng giới hạn bởi 
1B, 2C, 3D, 4A, 5D, 6C, 7B, 8A, 9B, 10, 11C, 12B, 13B, 14A
A. 	B. 	C. 	D. 
Tính thể khối tròn xoay.
Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành, đt x = a, đt x = b quay quanh trục hoành: 
Chú ý: Đối với thể tích ta không cần chia làm nhiều tích phân:
Câu 1: Tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đương đồ thị hàm số , trục hoành, đt x=0, đt x=1 quay quanh trục hoành.
Câu 2: Tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đương đồ thị hàm số , trục hoành, đt x=-1, đt x=0 quay quanh trục hoành.
Câu 3: Tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đương đồ thị hàm số , trục hoành, trục tung, đt x=1 quay quanh trục hoành.
Câu 4: Tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đương đồ thị hàm số , trục hoành quay quanh trục hoành.
Câu 5: Tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đương đồ thị hàm số , trục hoành, đt x=0, đt x= quay quanh trục hoành.
Câu 6: Tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi các đương đồ thị hàm số , trục hoành, trục tung, đt x= quay quanh trục hoành. 
Câu 7. Cho hình phẳng (H) giới hạn bởi các đường Tính thể tích khối tròn xoay tạo thành khi cho hình (H) quay quanh trục Ox. 
Câu 8. Cho hình phẳng (H) giới hạn bởi các đường Tính thể tích khối tròn xoay tạo thành khi cho hình (H) quay quanh trục Ox.
Câu 9. Cho hình phẳng (H) giới hạn bởi các đường Tính thể tích khối tròn xoay tạo thành khi cho hình (H) quay quanh trục Ox. 
Câu 10. Cho hình phẳng (H) giới hạn bởi các đường Tính thể tích khối tròn xoay tạo thành khi cho hình (H) quay quanh trục Ox.
Trắc nghiệm
Câu 1: Gọi D là miền giới hạn bởi và trục hoành. Tính thể tích vật thể tròn xoay khi quay D quanh trục Ox .
A. 	B. 	C. 	D. 
Câu 2: Tính thể tích khối tròn xoay khi quay quanh Ox miền D được giới hạn bởi .
A. 	B. 	C. 	D. 
Câu 3: Câu 3: Thể tích khối tròn xoay khi quay hình phẳng (D) : , quanh trục Ox là ( với là phân số tối giản). Khi đó M + N = 
A. 38 	B. 40	C. 28	D. 128
Câu 4: Tính thể tích khối tròn xoay khi quay quanh Ox miền D được giới hạn bởi . 
A. 	B. 	C. 	D. 
Câu 5: Tính thể tích khối tròn xoay khi quay hình phẳng (D) : , quanh trục oy
A. 	B. 	C. 	D. 
Câu 6: Một hình thang cong (H) giới hạn bởi đồ thị hàm số , trục ox và hai đường thẳng . Khi quay (H) quanh trục ox tạo thành một khối tròn xoay. Gọi V là thể tích khối tròn xoay đó. Phát biểu nào sau đây là đúng.
A. 	B. 	C. 	D. 
Câu 7: Tính thể tích khối tròn xoay khi quay hình phẳng (D) : , quanh trục Ox .
A. 	B. 	C. 	D. 
-
Câu 5: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục tung. 
A. 	B. 	C. 	D. 
Câu 6: 
A. 	B. 	C. 	D.