Toán học - Bài tập tết

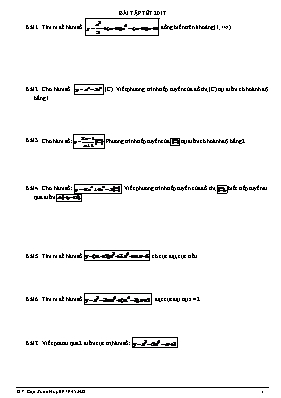
BÀI TẬP TẾT 2017
Tìm m để hàm số đồng biến trên khoảng (1; +¥).
Cho hàm số (C). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 1.
Cho hàm số: Phương trình tiếp tuyến của tại điểm có hoành độ bằng 2 
Cho hàm số: . Viết phương trình tiếp tuyến của đồ thị biết tiếp tuyến đi qua điểm 
Tìm m để hàm số có cực đại, cực tiểu 
Tìm m để hàm số đạt cực đại tại x = 2 
Viết ptđt đi qua 2 điểm cực trị hàm số: 
Tìm m để hàm số có đường thẳng đi qua 2 cực trị song song với đt: y = –4x + 1.
Tìm max, min của hàm số 
1. 	
2.	
3. 
Tìm max, min của hàm số: trên [–1; 5]	
Tìm m để phương trình có 4 nghiệm phân biệt 
Gọi có tung độ bằng . Tiếp tuyến của tại M cắt các trục tọa độ lần lượt tại A và B. Hãy tính diện tích tam giác ?
Cho . Tính log318 theo a
Cho . Tính a và b
Giải phương trình: 
Giải phương trình: 
Giải phương trình: 	
 Giải phương trình: 
 Giải phương trình 
Giải bất phương trình 
 Giải bất phương trình 
Giải bất phương trình 
Tính diện tích hình phẳng được giới hạn bởi đồ thị của hàm số trục hoành và hai đường thẳng x = - 1, x = 2 
Tính diện tích hình phẳng giới hạn bởi hai đường thẳng và đồ thị của hai hàm số 
Tính diện tích hình phẳng giới hạn bởi hai đường cong và 
Cho hình chóp đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với đáy một góc 60o. Thể tích của khối chóp đều
Cho hình chóp S.ABCD biết ABCD là một hình thang vuông ở A và D; AB = 2a; AD = DC = a. Tam giác SAD vuông ở S. Gọi I là trung điểm AD. Biết (SIC) và (SIB) cùng vuông góc với mp(ABCD). Thể tích khối chóp S.ABCD theo a bằng
Cho hình chóp đều , biết hình chóp này có chiều cao bằng và độ dài cạnh bên bằng . Tính thể tích khối chóp bằng:
Cho lăng trụ đứng ABC.A/B/C/ có đáy ABC là tam giác vuông tại B, AB=a, BC = , mặt bên (A/BC) hợp với mặt đáy (ABC) một góc 300 . Thể tích khối lăng trụ là
Cho hình chóp S.ABC có đáy ABC là hình tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA= . Khi đó khoảng cách từ A đến mp (SBC) bằng: