Toán - Hình học casio

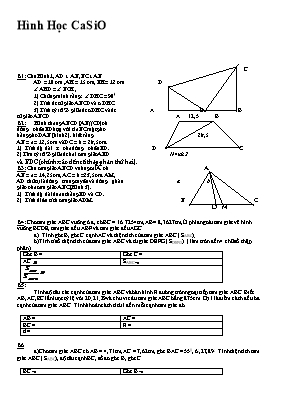
Hình Học CaSiO
	 C
B1: Cho H×nh 1, AD ^ AB, BC ^ AB
	AD = 10 cm , AE = 15 cm, BE = 12 cm 	 D
	Ð AED = Ð BCE ,
	1) Chøng minh r»ng: Ð DEC = 900
	2) TÝnh dt tø gi¸c ABCD vµ D DEC
	3) TÝnh tû sè % gi÷a dt D DEC vµ dt 	 A	 E 	B
tø gi¸c ABCD.	 A 12,5 B
B2:	 H×nh thang ABCD (AB//CD) cã 	 
®­êng chÐo BD hîp víi tia BC mét gãc 
b»ng gãc DAB (h×nh 2). biÕt r»ng 	 28,5
AB = a = 12,5 cm vµ DC = b = 28,5 cm.	
TÝnh ®é dµi x cña ®­êng chÐo BD. 	D	 C
2) T×m tû sè % gi÷a dt hai tam gi¸c ABD 	H×nh 2
vµ BDC (chÝnh x¸c ®Õn sè thËp ph©n thø hai)	.	
B3: Cho tam gi¸c ABCD vu«ng t¹i A cã 	 A
AB = a = 14,25 cm, AC = b =23,5 cm. AM,
AD thø tù lµ ®­êng trung tuyÕn vµ ®­êng ph©n 	 a b
gi¸c cña tam gi¸c ABC (H×nh 3).	 
TÝnh ®é dµi ®o¹n th¼ng BD vµ CD.
TÝnh diÖn tÝch tam gi¸c ADM.	 B	 C
 D M
B4: Cho tam giác ABC vuông ở a, có BC = 16.7254cm, AB= 8,3627cm, Ở phía ngoài tam giác vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC.
Tính góc B, góc C cạnh AC và diện tích của tam giác ABC ( SABC);
b)Tình tỉ số diện tích của tam giác ABC và tứ giác DEFG ( SDEFG). ( làm tròn đến 4 chữ số thập phân) 
Góc B =
Góc C =
AC 
SABC 
B5: 
Tính độ dài các cạnh của tam giác ABC và bán kính R đường tròn ngoại tiếp tam giác ABC. Biết AB,AC,BC lần lược tỷ lệ với 20;21;29 và chu vi cảu tam giác ABC bằng 875cm.Gọi I là điểm cách đều ba cạnh của tam giác ABC. Tính khoản cách d từ I đến mỗi cạnh tam giác đó
AB =
AC =
BC =
R =
d =
B6
a)Cho tam giác ABC có AB = 4,71cm, AC = 7,62cm, góc BAC = 550, 6;,27, 89;. Tính diện tích tam giác ABC ( SABC), độ dài cạnh BC, số đo góc B, góc C.
BC 
Góc B 
SABC 
Góc C 
Cho hinh thang ABCD ( BC//AD) , BC=10, 3752 cm, AD=12,4561 cm.O là giao điểm của hai đường chéo. Qua O kẻ một đường thẳng song song với BC cắt CD tại F.
	a)Tính OF ( chính xác đến bốn chữ số ở phần thập phân)
	b) Tính tỷ số phần trăm giữa diện tích tam giác AOD ( SAOD) và diện tích hình thang ABCD ( chính xác đến hai chữ số ở phần thập phân)
	Ghi kết quả tính được vào bảng sau:
OF
B7
cho hình chữ nhật ABCD (AB>BC).Qua B kẻ đường thẳng vuông góc với đường chéo CA tại H. cho BH=1,2547 cm; BAC=37028’50’’. Tính diện tích hình chữ nhật ABCD (SABCD)
SABCD 
b) cho tam giác ABC có B=1200 ;BC=12 cm; AB=6 cm.Phân giác trong của góc B cắt cạnh AC tại D. tính diện tích tam giác ABD(SABD).
SABD
B8
Cho tam giác ABC có AB=14,12cm; AC=15,34cm;Â =7125.
Tính diện tích tam giác ABC (S).Ghi kết quả gần đúng với 2 chữ số ở phần thập phân)
b) Trên cạnh AB lấy điểm M ,trên cạnh AC lấy điểm N sao cho AM=3BM và AN=4CN.BN và CM cắt nhau tại P.Tính diện tích tam giác APB (S).(Ghi kết quả gần đúng với 2 chữ số ở phần thập phân)
(S) ( S) 
Bài 9
Cho hình chữ nhật ABCD (AB>BC) và điểm M nằm trên đường chéo BD sao cho :
DAM =15.kẻ MI vuông góc AB (I AB). Cho biết MI=AB và CD =cm.
Tính góc MAC (độ, phút ,giây) và độ dài đoạn AD.
Góc MAC = AD 
B10: Hình chữ nhật ABCD có độ dài các cạnh AB = m, BC = n. 
Từ A kẻ AH vuông góc với đường chéo BD 
Tính diện tích tam giác ABH theo m, n
Cho biết m = 3,15 cm và n = 2,43 cm.
 Tính ( chính xác đến 4 chữ số thập phân) diện tích tam giác ABH 
B11: Hình thang vuông có góc nhọn , 
độ dài các cạnh 
Tính diện tích, chu vi và các đường chéo của hình thang 
theo và .
Tính ( chính xác đến 4 chữ số thập phân ) diện tích, chu vi và các 
đường chéo của hình thang với 
B12: (1 ®iÓm) Cho , . §­êng ph©n gi¸c cña c¾t t¹i D.
B12 §S 
a) BD=4,166666667 (cm)
b) 11,27637245(cm2) 
TÝnh ®é dµi ®o¹n th¼ng BD.
TÝnh diÖn tÝch 
B13 Cho tam gi¸c ABC gãc A = 410, ®é dµi c¹nh AB b»ng 2,04255 cm vµ AC =5,73522cm
Trªn c¹nh AB lÊy ®iÓm M sao cho AM = 0,84918 cm. Mét ®­êng th¼ng ®i qua M vµ träng t©m G cña tam gi¸c ABC c¾t canh AC t¹i N.
TÝnh AN.
TÝnh diÖn tÝch S cña tø gi¸c BMNC. 
AN 
 S 
B14 Tam giác ABC vuông tại A có cạnh AB = a = 2,75 cm, góc C = α = 37o25’. Từ A vẽ các đường cao AH, đường phân giác AD và đường trung tuyến AM.
Tính độ dài của AH, AD, AM.
Tính diện tích tam giác ADM.
(Kết quả lấy với 2 chữ số ở phần thập phân)
B15
Cho tam giác ABC có ba góc nhọn. Chúng minh rằng tổng của bình phương cạnh thứ nhất và bình phương cạnh thứ hai bằng hai lần bình phương trung tuyến thuộc cạnh thứ ba cộng với nửa bình phương cạnh thứ ba.
Bài toán áp dụng : Tam giác ABC có cạnh AC = b = 3,85 cm ; AB = c = 3,25 cm và đường cao AH = h = 2,75cm.
Tính các góc A, B, C và cạnh BC của tam giác. 
Tính độ dài của trung tuyến AM (M thuộc BC)
Tính diện tích tam giác AHM.
(góc tính đến phút ; độ dài và diện tích lấy kết quả với 2 chữ số phần thập phân.
B16a) Cho h×nh thang c©n ABCD (AB lµ c¹nh ®¸y nhá) vµ hai ®­êng chÐo AC, BD vu«ng gãc víi nhau, AB =15,34 cm, AD =BC =20,35cm. TÝnh diÖn tÝch h×nh thang c©n ABCD vµ c¹nh ®¸y CD.
b) Cho tam gi¸c ABC (A = 900), AB = 3,74 , AC = 4,51;
TÝnh ®­êng cao AH, vµ tÝnh gãc B theo ®é phót gi©y;
§­êng ph©n gi¸c kÎ tõ A c¾t BC t¹ D. TÝnh AD vµ BD.
B17 / Cho nh×nh vu«ng ABCD cã ®é dµi c¹nh lµ a=. Gäi I lµ trung ®iÓm cña AB. §iÓm H thuéc DI sao cho gãc AHI = 90o. 
	a)TÝnh diÖn tÝch tam gi¸c CHD. Tõ ®ã suy ra diÖn tÝch tø gi¸c BCHI.
	b)Cho I tïy ý thuéc AB, M tïy ý thuéc BC sao cho gãc MDI = 45o. TÝnh gi¸ trÞ lín nhÊt cña diÖn tÝch tam gi¸c DMI.
 B18/ Cho h×nh thang ABCD(AB//CD) cã . TÝnh AD;BC vµ ®­êng cao cña ht
B19 / Cho h×nh th·ng c©n ABCD cã hsi ®­êng chÐo vu«ng gãc, ®¸y nhá AB=13,724; c¹nh bªn 21, 827. TÝnh diÖn tÝch h×nh th·ng( chÝnh x¸c ®Õn 0, 0001)
B20 / Cho tam gi¸c vu«ng ABC cã AB = ; AC = . Gäi M , N , P thø tù lµ trung ®iÓm cña BC ; AC vµ AB. TÝnh tû sè chu vi cña DMNP vµ chu vi cña DABC ? ( ChÝnh x¸c ®Õn 6 ch÷ sè thËp ph©n)
B 21/ Cho tam gi¸c ABC cã gãc B = 450, gãc C=60o, BC=5cm. TÝnh chu vi tam gi¸c ABC.
B22 / Cho h×nh thang ABCD (AB//CD) cã ®­êng chÐo BD hîp víi BC mét gãc b»ng gãc DÂB. BiÕt 
AB = a = 12,5cm ; DC = b = 28,5cm. TÝnh:
§é dµi cña ®­êng chÐo BD ?
TØ sè gi÷a diÖn tÝch DABD vµ diÖn tÝch DBCD ?
B23/
Tø gi¸c ABCD cã I lµ giao ®iÓm cña hai ®­êng chÐo. TÝnh AD biÕt r»ng AB = 6; IA = 8; IB = 4; 
ID = 6.
B 24 /
TÝnh c¸c c¹nh cña h×nh ch÷ nhËt biÕt r»ng ®­êng vu«ng gãc kÎ tõ mét ®Ønh ®Õn mét ®­êng chÐo chia ®­êng chÐo ®ã thµnh hai ®o¹n th¼ng cã ®é dµi lµ 9 cm vµ 16 cm ?
B25/: Tam giaùc ABC coù , AB = 6,25cm , BC = 12,50cm . Ñöôøng phaân giaùc cuûa goùc B caét AC taïi D . 
Tính ñoä daøi cuûa ñoaïn thaúng BD .
Tính tyû leä dieän tích cuûa caùc tam giaùc ABD vaø ABC . 
Tính dieän tích tam giaùc ABD ( cho bieát ) 
	Tính vaø ghi keát quaû vaøo oâ vuoâng : 
BD = 
= 
= 
B26:/ Cho tam giaùc ABC coù caùc caïnh AB = 21cm , AC = 28cm , BC = 35cm .
Chöùng minh tam giaùc ABC vuoâng ? Tính dieän tích tam giaùc ABC ? 
Tính caùc goùc B vaø C ( ñoä , phuùt , giaây ) 
Ñöôøng phaân giaùc cuûa goùc A caét caïnh BC taïi D . Tính DB , DC ? 
Ñieàn caùc keát quaû tính vaøo oâ vuoâng : 
a) 
DB = 
DC = 
 B27/: Tính dieän tích xung quanh vaø theå tích cuûa hình choùp töù giaùc ñeàu SABCD , bieát caïnh ñaùy AD = 16,157 cm , caïnh beân SC = 17,504cm ? 
B28/: Cho tam giaùc ABC coù AB = 3,75cm ; BC = 5,95cm vaø . Qua trung ñieåm M cuûa AB vaø N cuûa AC keû MH vaø NK vuoâng goùc vôùi CB . Tính dieän tích töù giaùc NMHK ? 
Ñieàn caùc keát quaû tính vaøo oâ vuoâng : 
B29/: Cho hình thang caân coù hai ñöôøng cheùo vuoâng goùc vôùi nhau . Hai ñaùy coù ñoä daøi 15,34cm vaø 24,35cm . 
Tính dieän tích ht? Tính chu vi ht ?
B30/ : Cho tam giaùc ABC coù ñöôøng cao AH = 21,431cm , HB = 7,384cm vaø HC = 9,318cm.
Tính AB , AC ? 
Tính dieän tích ABC ? 
Tính goùc A ( ñoä , phuùt , giaây ) vaø söû duïng coâng thöùc 
B31/ : a) Cho tam giaùc ABC coù ñöôøng cao AH , bieát AB = 4cm , BC = 5cm , CA = 6cm . Tính AH vaø CH ? 
	 b) Tính dieän tích xung quanh vaø theå tích cuûa hình choùp ñeàu SABC , bieát chieàu cao SO = 12,589 cm ; caïnh ñaùy AB = cm ? 
Ghi keát quaû vaøo oâ vuoâng
 AH =
CH = 
Baøi 32/: a) Tính soá ño caùc goùc cuûa tam giaùc ABC bieát 
	 b) Tam giaùc ABC coù . Tính ñoä lôùn cuûa goùc C ( ñoä , phuùt , giaây ) 
 c) Cho tam giaùc ABC vuoâng taïi B , caïnh BC = 18,6 cm ; hai trung tuyeán BM vaø CN vuoâng goùc vôùi nhau . Tính CN ( chính xaùc ñeán chöõ soá thaäp phaân thöù tö ) ? 
Haõy ñieàn caùc keát quaû tính ñöôïc vaøo oâ vuoâng . 
a) 
b) 
c) CN = 
Cho tam giaùc ABC coù AB = 1,05 ; BC = 2,08 ; AC = 2,33 . Tính ñöôøng cao BH vaø dieän tích tam giaùc ABC gaàn ñuùng vôùi 4 chöõ soá thaäp phaân ? ( Söû duïng coâng thöùc Heâ – roâng trong tam giaùc ABC : vôùi )
Baøi 33/: Cho tam giaùc ABC vuoâng taïi A , coù AB = 6,251cm vaø . 
Tính BC , AC vaø ? 
Tính AH vaø dieän tích tam giaùc ABC ? 
Tính trung tuyeán AM vaø phaân giaùc AD cuûa tam giaùc ABC ? 
Haõy ñieàn caùc keát quaû tính ñöôïc vaøo oâ vuoâng . 
BC = 
AC = 
 = 
AH = 
AM = 
AD = 
Baøi 34/ : Moät hình thoi coù caïnh baèng 24,13cm , khoaûng caùch giöõa hai caïnh laø 12,25cm . 
Tính caùc goùc cuûa hình thoi ? ( ñoä , phuùt , giaây )
Tính dieän tích cuûa hình troøn (O) noäi tieáp hình thoi chính xaùc ñeán chöõ soá thaäp phaân thöù ba ? 
Tính dieän tích tam giaùc ñeàu ngoaïi tieáp ñöôøng troøn (O) ? 
Ghi keát quaû vaøo oâ vuoâng
S(O) = 
Stam giaùc ñeàu = 
Baøi 35/: Cho tam giaùc ABC coù AB = 6,3031cm; AC = 5,9652cm ; BC = 8,35cm. Keû ñöôøng cao AH cuûa tam giaùc ABC . 
Tính BH , HC vaø AH ? 
Tính caùc goùc cuûa tam giaùc ABC ? ( ñoä , phuùt ,giaây ) 
Tính ñoä daøi baùn kính ñöôøng troøn noäi tieáp r cuûa tam giaùc ABC ? 
Haõy ñieàn caùc keát quaû tính ñöôïc vaøo oâ vuoâng . 
BH = 
HC = 
AH = 
r =
B36 /: Cho tam gi¸c ABC cã , AB= 6,25 cm, BC=2AB. §­êng ph©n gi¸c cña gãc B c¾t AC t¹i D.
 a/ TÝnh ®é dµi BD
 b/ TÝnh diÖn tÝch tam gi¸c ABD
B37 /: Tam giaùc ABC vuoâng taïi A AB = c = 23,82001 cm ; AC = b =29,1945 cm. Goïi G laø troïng taâm . 
 A’ ; B’ ; C’ laø hình chieáu cuûa G xuoáng caùc caïnh BC , CA , AB . Goïi S vaø S’ laàn löôït laø dieän tích 
 cuûa hai tam giaùc ABC vaø A’B’C’.
Tính tyû soá 
Tính S’.