Toán 8 - Tiết 25: Kiểm tra chương I

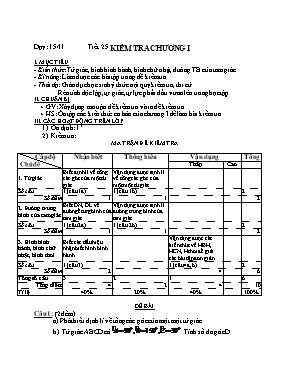
Dạy: 15/11 Tiết 25 KIỂM TRA CHƯƠNG I
I. MỤC TIÊU
- Kiến thức: Tứ giác, hình bình hành, hình chữ nhật, đường TB của tam giác.
- Kĩ năng: Làm được các bài tập trong đề kiểm tra.
- Thái độ: Giáo dục học sinh ý thức nội quy kiểm tra, thi cử.
 Rèn tính độc lập, tự giác, tự lực phấn đấu vươn lên trong học tập. 	
II. CHUẨN BỊ
+ GV: Xây dựng ma trận đề kiểm tra và ra đề kiểm tra.
+ HS: Ôn tập các kiến thức cơ bản của chương I để làm bài kiểm tra.
III. CÁC HOẠT ĐỘNG TRÊN LỚP
Ổn định: 1’
Kiểm tra:
MA TRẬN ĐỀ KIỂM TRA
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
 Vận dụng
Tổng
Thấp
Cao
1. Tứ giác
Biết định lí về tổng các góc của một tứ giác
Vận dụng được định lí về tổng các góc của một một tứ giác
Số câu
1 (câu 1a)
1 (câu 1b)
2
Số điểm
1
1
2
2. Đường trung bình của tam giác
Biết ĐN, ĐL về đườngểtung bình của tam giác
Vận dụng được định lí đường trung bình của tam giác
Số câu
1 (câu 2a)
1 (câu 2b)
2
Số điểm
1
1
2
3. Hình bình hành, hình chữ nhật, hình thoi
Biết các dấu hiệu nhận biết hình bình hành
Vận dụng được các kiến thức về HBH, HCN, Hthoi để giải các bài tập đơn giản
Số câu
1 (câu 3)
1 (câu 4a, b)
2
Số điểm
2
4
6
Tổng số câu
3
2
1
6
Tổng điểm
4
2
4
10
Tỉ lệ
40%
20%
40%
100%
ĐỀ BÀI
Câu 1: (2điểm)
a) Phát biểu định lí về tổng các góc của một một tứ giác.
b) Tứ giác ABCD có . Tính số đo góc D.
Câu 2: (3điểm) 
a) Phát biểu định nghĩa, tính chất đường trung bình của tam giác.
b) Cho tam giác ABC, D là trung điểm của cạnh AB, E là trung điểm của cạnh AC. Tính độ dài cạnh BC, biết DE = 4cm.
Câu 3: (2điểm)
Nêu các dấu hiệu nhận biết hình bình hành.
Câu 4: (3điểm)
Cho tam giác ABC vuông tại A, D là trung điểm của cạnh BC. Gọi M là điểm đối xứng với D qua AB, N là điểm đối xứng với D qua AC. Gọi E là giao điểm của DM và AB. Gọi F là giao điểm của DN và AC.
Tứ giác AEDF là hình gì? Vì sao?
Các tứ giác ADBM, ADCN là hình gì? Vì sao?
ĐÁP ÁN VÀ BIỂU ĐIỂM
Câu
Nội dung
Điểm
1
(2điểm)
a) Định lí: Tổng các góc của một tứ giác bằng 3600.
b) 3600 – (900 + 1500 + 300) = 900 
1đ
1đ
2
(2điểm)
a) Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
 Tính chất : Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nữa cạnh ấy. 
b) DE là đường trung bình của tam giác ΔABC =>BC =2.DE =2.4=8(cm)
0.5đ
0.5đ
1đ
3
(2điểm)
Các dấu hiệu nhận biết hình bình hành: ( 5 dấu hiệu)
1. Tứ giác có các cạnh đối song song là hình bình hành. 
2. Tứ giác có các cạnh đối bằng nhau là hình bình hành. 
3. Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. 
4. Tứ giác có các góc đối bằng nhau là hình bình hành. 
5. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
2đ
4
(4điểm)
GT
	ΔABC,= 900, BD = DC, ABDM = {E}, DE = EM,
 	ABDM, ACDN = {F}, ACDN, DF=FN
KL
 a) Tg AEDF là hình gì? Vì sao?
 b) Các tg ADBM, ADCN là hình gì ? Vì sao?
Giải:
a) Tg EDF là hình chữ nhật 
Vì: = 900; AB ^ DM tại E => = 900, 
 AC ^ DN tại F => = 900	 
b) ΔABC có: AD = BD = DC (trung tuyến bằng nửa cạnh huyền) 
 => ΔABD cân tại D có DE là đường cao => EA = EB
 Mà: DE = EM (D đối xứng với M qua AB) 	
 => Tg ADBM là hình thoi (có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau)
Tương tự tứ giác ADCN là hình thoi.	
0.25
0.75đ
1đ
2đ
Ghi chú: HS làm cách khác đúng vẫn cho điểm tối đa.