Tài liệu máy tính cầm tay 9

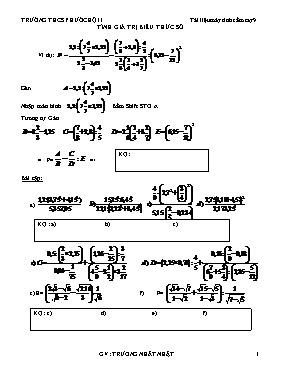
TÍNH GIÁ TRỊ BIỂU THỨC SỐ
	Ví dụ: 
Gán 
Nhập màn hình Bấm Shift STO A 
Tương tự Gán 
KQ : 
P= => 
Bài tập:
KQ : a) 	b) 	c)
a) 
e) E=	f) 	F=
KQ : c) 	d) 	e) f)
Sè thËp ph©n v« h¹n tuÇn hoµn.
 + D¹ng tuÇn hoµn ®¬n: 
+ D¹ng tuÇn hoµn t¹p:
 (bao nhiªu b bÊy nhieu sè 9 bao nhiªu a bÊy nhiªu sè 0)
Nhaän xeùt :
=0,(1); =0,(01); =0,(009); =0,(0009)
KQ : 
Thöïc hieän caùc pheùp tính:
KQ : 
a. 
b. 
KQ : 
c. 
KQ : 
d. 
KQ : 
e. 
KQ : 
f. 
TÍNH GIÁ TRỊ BIỂU THỨC SỐ CÓ CHỨA CĂN 
VD: M = tại x = 4
Giải: 
Nhập màn hình	ˆ ( 6 alpha A + 1 ) x2 	x ( alpha A x2 + 9 ) x3 
bấm	4 shift sto A (gán 4 cho A)
= kết quả: 29
KQ : 
Bài tập:
A = 	tại x = 4	
KQ : 
B = 	tại x = 3	
KQ : 
C = 	tại x = -1/2 	
KQ : 
	D = khi x = 2 + 3	
KQ : 
KQ : 
TÍNH GIÁ TRỊ PHẦN TRĂM CỦA MỘT BIỂU THỨC
KQ : 
a) Tìm 25% của 	Tính tử=A và mẫu =B => (A:B).25%
KQ : 
b) Tìm 15% của 
KQ : 
c) Tìm 2,25% của 	
KQ : 
d) Tìm 5% của 
TÍNH GÍA TRỊ BIỂU THỨC TRONG LIÊN PHÂN SỐ
Tính giá trị của các biểu thức sau và biểu diễn kết quả dưới dạng phân số:
Giải: Ấn 3 x-1 x 5 + 2 =
x-1 x 4 + 2 =
x-1 x 5 + 2 =
x-1 x 4 + 2 =
x-1 x 5 + 3 =
Kết quả: 4,6099644
Vd: E = 
a) 	b) 
KQ : 
KQ : 
KQ : 
KQ : 
c) 	d) 
TÌM x, y TRONG LIÊN PHÂN SỐ
Giải: 15┘17 =
ấn tiếp x-1 = 1┘2┘15
ấn tiếp - 1 = 2┘15
ấn tiếp x-1 = 7┘1┘2
Kết quả: x = 7; y = 2
VD1: 	
Bài tập 1: Tìm a và b
KQ : 
KQ : 
KQ : 
Bài tập 2: tìm x và y
KQ : 
KQ : 
Hướng dẫn: Đặt A = , B = 
Ta có 4 + Ax = Bx. Suy ra .
Bài tập 3: Cho . Viết lại 
Viết kết quả theo thứ tự 
Giải:
Ta có 
 . 
Tiếp tục tính như trên, cuối cùng ta được:
Viết kết quả theo ký hiệu liên phân số 
GIẢI PHƯƠNG TRÌNH
KQ : 
(2,5 + 3x). 1,5 = 4,28 – (4,3 + 5,423)
KQ : 
KQ : 
KQ : 
d) 
KQ : 
e) 
KQ : 
 f) 
KQ : 
 h) 	
KQ : 
i) 	
TÍNH GIÁ TRỊ BIỂU THỨC
Ví dụ: Tính giá trị biểu thức 3x2 + 7x – 5 tại x = 2
	Ấn:	 2 shift sto X
	Ấn:	 alpha X2 x 3 + 7 alpha X - 5 =	Kết quả: 21
KQ : 
Áp dụng:
a) 3x4 – 4x3 – 7x2 – 9x + 2,5	Tại x = 2,15
KQ : 
b) x9 – 3x7 + 2x6 – 2,13x4 + x3 – 3,12x + 13,478	Tại x = -5,123
KQ : 
c) 	Tại x = 
KQ : 
d) 2x10 – 3x8 + 5x7 – 4x5 + x3 – 7x – 3,147	Tại x = 
TÍNH GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC ( CHÍNH XÁC ĐẾN 0,0001)
KQ : 
KQ : 
KQ : 
KQ : 
D = (tg25015’ – tg15027’). Cotg35025’ – cotg278015’ 
KQ : 
E = 	
TÍNH GIÁ TRỊ BIỂU THỨC BIẾT TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN 
KQ : 
	a) Biết sin= 0,3456 	Tính 
KQ : 
	b) Biết cos3= 0,5678	Tính 
c) Biết tg (0< x < 900)
	Tính 
KQ : 
TÌM SỐ DƯ CỦA PHÉP CHIA SỐ NGUYÊN
Khi đề cho số bé hơn 10 chữ số:
 Số bị chia = số chia . thương + số dư (a = bq + r) (0 < r < b)
 Suy ra r = a – b . q
Số dư của A chia cho B bằng A – B * phần nguyên của (A : B).
Ví dụ : Tìm số dư của phép chia 9124565217 : 123456
Ghi vào màn hình 9124565217 : 123456 ấn =
máy hiện thương số là 73909,45128
Đưa con trỏ lên dòng biểu thức sửa lại là
9124565217 - 123456 * 73909 = 
Kết quả: Số dư là 55713
b) Khi đề cho số lớn hơn 10 chữ số:
 Phương pháp: 
Tìm số dư của A khi chia cho B ( A là số có nhiều hơn 10 chữ số)
Cắt ra thành 2 nhóm , nhóm đầu có chín chữ số (kể từ bên trái). Tìm số dư phần đầu khi chia cho B.
Viết liên tiếp sau số dư phần còn lại (tối đa đủ 9 chữ số) rồi tìm số dư lần hai. 
Nếu còn nữa tính liên tiếp như vậy.
Ví dụ: Tìm số dư của phép chia 2345678901234 cho 4567.
Ta tìm số dư của phép chia 234567890 cho 4567: Được kết quả số dư là : 2203
Tìm tiếp số dư của phép chia 22031234 cho 4567.
Kết quả số dư cuối cùng là 26.
Bài tập: Tìm số dư của các phép chia:
983637955 cho 9604325
987896854 cho 698521
143946789034568 cho 134578 
1234567890987654321 : 123456
c) Dùng kiến thức về đồng dư để tìm số dư.
* Phép đồng dư: 
+ Định nghĩa: Nếu hai số nguyên a và b chia cho c (c khác 0) có cùng số dư ta nói a đồng dư với b theo modun c ký hiệu 
+ Một số tính chất: Với mọi a, b, c thuộc Z+
Ví dụ 1: Tìm số dư của phép chia 126 cho 19
Giải:
Vậy số dư của phép chia 126 cho 19 là 1
Ví dụ 2: Tìm số dư của phép chia 2004376 cho 1975
Giải:
Biết 376 = 62 . 6 + 4
Ta có:
Vậy 
Kết quả: Số dư của phép chia 2004376 cho 1975 là 246
Bài tập thực hành:
Tìm số dư của phép chia :
138 cho 27 	Kq : .
2514 cho 65	Kq : .
197838 cho 3878.	Kq : .
20059 cho 2007	Kq : .
715 cho 2001	Kq : .
d/ Tìm soá dö an cho b 
Tuyø vaøo soá muõ cuûa a ñeå phaân tích, tìm moät soá a’ thích hôïp (Khoâng laøm traøn maùy) roài tìm soá dö cuûa a’ cho b. Tieáp tuïc laøm nhö vaäy cho ñeán cuoái cuøng.
Ñeå tìm soá dö an cho b ta laøm nhö nhau:
-Neáu a chia cho b thöông laø q; dö laø r ta coù: a=bq+r 
 (Coâng thöùc naøy khoâng quan taâm ñeán heä soá cuûa caùc soá haïng khi khai trieån)
Vaäy chæ tìm xem rn chia cho b dö laø maáy.
VD: Tìm soá dö cuûa 1112 cho 2001.
Giaûi: 
116=1771561 khi chia cho 2001 dö laø 676.
Vì 1112=(116)2 chia cho 2001 dö laø: 6762:2001 dö laø 748
Vaäy dö cuûa pheùp chia treân laø 784.
Baøi taäp aùp duïng: 
Tìm soá dö trong pheùp chia a cho b:
Ñaùp soá 
Ñaùp soá 
1/ a=736; b=2003.	2/ a=7218 ; b=2009.363
Ñaùp soá 
3/ a= 1318+1320; b=6954
Ñaùp soá 
4/ a=1358+2475 ; b= 3311
CÁC BÀI TOÁN VỀ : “ PHÉP NHÂN TRÀN MÀN HÌNH ”
Bài 1: 
Tính chính xác tổng S = 1.1! + 2.2! + 3.3! + 4.4! + ... + 16.16!.
Giải: 
Vì n . n! = (n + 1 – 1).n! = (n + 1)! – n! nên:
S = 1.1! + 2.2! + 3.3! + 4.4! + ... + 16.16! = (2! – 1!) + (3! – 2!) + ... + (17! – 16!)
S = 17! – 1!.
Không thể tính 17 bằng máy tính vì 17! Là một số có nhiều hơn 10 chữ số (tràn màn hình). Nên ta tính theo cách sau:
Ta biểu diễn S dưới dạng : a.10n + b với a, b phù hợp để khi thực hiện phép tính, máy không bị tràn, cho kết quả chính xác.
Ta có : 17! = 13! . 14 . 15 . 16 . 17 = 6227020800 . 57120
Lại có: 13! = 6227020800 = 6227 . 106 + 208 . 102 nên 
S = (6227 . 106 + 208 . 102) . 5712 . 10 – 1 = 6227 . 106 . 5712 . 10 + 208 . 102 . 5712 . 10 – 1 
 = 35568624 . 107 + 1188096 . 103 – 1 
Tính trên giấy:
3
5
5
6
8
6
2
4
0
0
0
0
0
0
0
1
1
8
8
0
9
6
0
0
0
3
5
5
6
8
7
4
2
8
0
9
6
0
0
0
 = 355687428096000 – 1 
 = 355687428095999.
Bài 2: 
Tính kết quả đúng của các tích sau:
M = 2222255555 . 2222266666.
N = 20032003 . 20042004.
Giải:
Đặt A = 22222, B = 55555, C = 666666.
Ta có M = (A.105 + B)(A.105 + C) = A2.1010 + AB.105 + AC.105 + BC
Tính trên máy:
A2 = 493817284 ; AB = 1234543210 ; AC = 1481451852 ; BC = 3703629630
Tính trên giấy:
A2.1010
4
9
3
8
1
7
2
8
4
0
0
0
0
0
0
0
0
0
0
AB.105
1
2
3
4
5
4
3
2
1
0
0
0
0
0
0
AC.105
1
4
8
1
4
5
1
8
5
2
0
0
0
0
0
BC
3
7
0
3
6
2
9
6
3
0
M
4
9
3
8
4
4
4
4
4
3
2
0
9
8
2
9
6
3
0
Đặt X = 2003, Y = 2004. Ta có:
N = (X.104 + X) (Y.104 + Y) = XY.108 + 2XY.104 + XY
Tính XY, 2XY trên máy, rồi tính N trên giấy như câu a)
Kết quả: 
M = 4938444443209829630.
N = 401481484254012.
Bài 3 : Tính 8567899 * 654787
Giải : Ta có 8567899 * 654787 = (8567 * 103 + 899) * (654 * 103 + 787)
= 8567 * 103 * 654 * 103 + 8567 * 103 * 787 + 899 * 654 * 103 + 899 * 787 
Tính trên giấy:
8567 * 103 * 654 * 103 = 5 602 818 000 000
 8567 * 103 * 787 	 = 6 742 229 000
899 * 654 * 103	 = 587 946 000 
899 * 787 = 707 513
Cộng dọc ta được 5 610 148 882 513 
Bài tập 
Tính chính xác các phép tính sau:
A = 20!. 	Kq : .
B = 5555566666 . 6666677777	Kq : .
C = 20072007 . 20082008	Kq : .
N = 13032006 * 13032007	Kq : .
10384713	Kq : .
201220032	Kq : . 
TÌM CHỮ SỐ HÀNG ĐƠN VỊ, HÀNG CHỤC, HÀNG TRĂM... CỦA MỘT LUỸ THỪA:
Bài 1: Tìm chữ số hàng đơn vị của số 172002 ( tức là tìm số dư của luỹ thừa khi chia cho 10 )
KQ : 
Bài 2: Tìm chữ số hàng chục của số 232005.( tức là tìm số dư của luỹ thừa khi chia cho 100 )
KQ : 
Bài 3: Tìm chữ số hàng trăm của số 232005 ( tức là tìm số dư của luỹ thừa khi chia cho 1000 )
KQ : 
Bài 4: Tìm 2 chữ số cuối cùng của tổng : A = 22000 + 22001 + 22002 
HD : A = 22000 (1 + 21 + 22 ) = 7.22000 ( rồi tìm số dư của luỹ thừa khi chia cho 100)
 KQ : 
Bài 5: Tìm 2 chữ số cuối cùng của tổng : A = 22000 + 22001 + 22002 + 22003 + 22004 + 22005 + 22006 
KQ : 
TÍNH SỐ LẺ THẬP PHÂN THỨ N SAU DẤU PHẨY.
 - Ta tìm chu kỳ của số thập phân là bao nhiêu.
- Tìm số dư của số thập phân thứ n khi chia cho số chu kỳ .
- Số dư chính là vị trí của số thập phân n 
Ví dụ 1: 
Tìm chữ số lẻ thập phân thứ 105 của phép chia 17 : 13
Giải:
Bước 1:
+ Thực hiện phép chia 17 : 13 = 1.307692308 (thực chất máy đã thực hiện phép tính rồi làm tròn và hiển thị kết quả trên màn hình)
Ta lấy 7 chữ số đầu tiên ở hàng thập phân là: 3076923
+ Tiếp theo tìm số dư của phép chia 
17 – 13* 1.3076923= 1.10-7 
Bước 2: 
+ lấy 1 : 13 = 0,07692307692
11 chữ số ở hàng thập phân tiếp theo là: 07692307692
Vậy ta đã tìm được 18 chữ số đầu tiên ở hàng thập phân sau dấu phẩy là:
307692307692307692
Vậy 17 : 13 = 1,(307692) Chu kỳ gồm 6 chữ số.
Ta có 105 = 6.17 + 3 ()
Vậy chữ số thập phân thứ 105 sau dấu phẩy là chữ số thứ ba của chu kỳ. Đó chính là số 7
Ví dụ 2:
Tìm chữ số thập phân thứ 132007 sau dấu phẩy trong phép chia 250000 cho 19
Giải:
Ta có . Vậy chỉ cần tìm chữ số thập phân thứ 132007 sau dấu phẩy trong phép chia 17 : 19
Bước 1: 
Ấn 17 : 19 = 0,8947368421. 
Ta được 9 chữ số đầu tiên sau dấu phẩy là 894736842
+ Lấy 17 – 0, 894736842 * 19 = 2 . 10-9
Bước 2:
Lấy 2 : 19 = 0,1052631579. 
Chín số ở hàng thập phân tiếp theo là: 105263157
+ Lấy 2 – 0,105263157 * 19 = 1,7 . 10-8 = 17 . 10-9
Bước 3:
Lấy 17 : 19 = 0,8947368421.
Chín số ở hàng thập phân tiếp theo là 
+ Lấy 17 – 0,0894736842 * 19 = 2 . 10-9
Bước 4: 
Lấy 2 : 19 = 0,1052631579. 
Chín số ở hàng thập phân tiếp theo là: 105263157
...
Vậy 17 : 19 = 0, 894736842105263157894736842105263157 ...
 = 0,(894736842105263157) . Chu kỳ gồm 18 chữ số.
Ta có 
Kết quả số dư là 1, suy ra số cần tìm là sồ đứng ở vị trí đầu tiên trong chu kỳ gồm 18 chữ số thập phân.
Kết quả : số 8
Bài tập:
Tìm chữ số thập phân thứ 2007 sau dấu phẩy khi chia:
1 chia cho 49 KQ : .
10 chia cho 23 KQ : .
IV. CÁC BÀI TOÁN VỀ ĐA THỨC
Một số kiến thức cần nhớ:
Định lý Bezout
Số dư trong phép chia f(x) cho nhị thức x – a chính là f(a)
Hệ quả: Nếu a là nghiệm của f(x) thì f(x) chia hết cho x – a
Sơ đồ Hor nơ
Ta có thể dùng sơ đồ Hor nơ để thìm kết quả của phép chia đa thức f(x) cho nhị thức x – a.
Ví dụ:
Thực hiện phép chia (x3 – 5x2 + 8x – 4) cho x – 2 bằng cách dùng sơ đồ Hor nơ.
Bước 1: Đặt các hệ số của đa thức bị chia theo thứ tự vào các cột của dòng trên.
a = 2
-5
8
-4
1
Bước 2: Trong 4 cột để trống ở dòng dưới, ba cột đầu cho ta các hệ số của đa thức thương, cột cuối cùng cho ta số dư.
Số thứ nhất của dòng dưới = số tương ứng ở dòng trên
Kể từ cột thứ hai, mỗi số ở dòng dưới được xác định bằng cách lấy a nhân với số cùng dòng liền trước rồi cộng với số cùng cột ở dòng trên
( Ta lấy 2.1+(-5) = -3 ; lấy 2.(-3)+8 = 2 ; lấy 2.2+(-4) = 0 )
a = 2
-5
8
-4
1
1
-3
2
0
Vậy (x3 – 5x2 + 8x – 4) = (x – 2)(x2 – 3x + 2) + 0
* Nếu đa thức bị chia là a0x3 + a1x2 + a2x + a3 , đa thức chia là x – a, ta được thương là b0x2 + b1x + b2 dư là r. Theo sơ đồ Hor nơ ta có:
a1
a3
a2
a0
r
b2
b1
a 
b0
ab2 + a3
ab1 + a2
ab0 + a1
a0
Một số dạng bài tập thường gặp :
1)Tìm số dư trong phép chia đa thức P(x) cho (x – a)
Cơ sở lý luận : P(x) = Q(x) . (x – a ) + r
Khi x = a thì r = P(a)
Ví dụ: Tìm số dư trong phép chia sau: f(x) = x3 – 9x2 – 35x + 7 cho x – 3.
Cách 1 : Tức là ta tính f(3) , số 3 là nghiệm của phương trình x – 3=0.
f(3) = 33 – 9.32 – 35.3 + 7 = -152
Vậy số dư trong phép chia sau: f(x) = x3 – 9x2 – 35x + 7 cho x – 3 là -152.
Cách 2 : Sử dụng sơ đồ Hor nơ
a = 3
-9
-35
7
1
1
-6
-53
-152
Vậy số dư trong phép chia sau: f(x) = x3 – 9x2 – 35x + 7 cho x – 3 là -152.
2) Điều kiện để P(x) chia hết cho (x – a )
P(x) + m (x – a ) 
Ví dụ 1 : 
Tìm giá trị của m để sao cho đa thức P(x) = 3x3 – 4x2 + 5x + 1 +m chia hết cho (x – 2 )
Tìm giá trị của m để đa thức P(x) = 2x3 – 3x2 – 4x + 5 + m chia hết cho (2x – 3)
Giải :a) Gọi P1(x) = 3x3 – 4x2 + 5x + 1 , ta có:
P(x) = P1(x) + m
Vậy P(x) hay P1(x) + m chia hết cho (x – 2) khi m = - P1(2)
Tính P1(2) :
Ấn 3 * 23 – 4 * 22 + 5 * 2 + 1 = 
P1(2) = 19 . Vậy m = - 19 
Gọi P1(x) = 2x3 – 3x2 – 4x + 5 , ta có : 
P(x) = P1(x) + m
Vì P(x) chia hết cho (2x +3) nên ta có P(
Tính P1(
Ấn 2 * - 3 * 
KQ : P1(= -2,5 
Ví dụ 2 : Cho hai đa thức 3x2 – 4x +5 + m và x3 + 3x2 – 5x + 7 + n . Hỏi với điều kiện nào của m và n thì hai đa thức có nghiệm chung a ?
Giải :
Gọi P(x) = 3x2 – 4x +5 ; Q(x) = x3 + 3x2 – 5x + 7.
Đa thức P(x) + m và đa thức Q(x) + n có nghiệm chung là a khi m = - P(a) và n = - Q(a)
Áp dụng vào bài toán trên với nghiệm chung là a = 0,5
KQ : P(0,5) = 3,75 . Vậy m = -3,75
 Q(0,5) = 5,375 . Vậy n = - 5,375.
Bài tập 
Bài 1: Tìm số dư trong phép chia 
a) x3 – 9x2 – 35x + 7 cho x – 12.
b)x3 – 3,256 x + 7,321 cho x – 1,1617.
c) 
 d)
Bài 2: Tìm a để x4 + 7x3 + 2x2 +13x + a chia hết cho x + 6
Bài 3: Cho P(x) = 3x3 + 17x – 625
a) Tính P(.
b) Tính a để P(x) + a2 chia hết cho x + 3
Bài 4: Chứng tỏ rằng đa thức sau chia hết cho x + 3
P(x) = 3x4 – 5x3 + 7x2 – 8x – 465.
Bài 5: Cho hai đa thức P(x) = x4 +5x3 – 6x2 + 3x +m và Q(x) = 5x3 – 4x2 + 3x + 2n.
a) Tìm giá trị của m và n để P(x) và Q(x) cùng chia hết cho x – 3 .
b) Với m và n vừa tìm được , hãy giải phương trình P(x) - Q(x) = 0 
Bài 6: T×m c¸c gi¸ trÞ cña m ®Ó ®a thøc P(x) = 2x3 + 3x2 - 4x + 5 + m chia hÕt cho 
 Q(x) = 3x +2
Bài 7: Cho hai ®a thøc P(x) = 3x2 - 4x + 5 + m; Q(x) = x3 + 3x2 - 5x + 7 + n. 
T×m m, n ®Ó hai ®a thøc trªn cã nghiÖm chung 
Bài 8: Cho phương trình : 2,5x5 – 3,1x4 +2,7x3 +1,7x2 – (5m – 1,7)x + 6,5m – 2,8 có một nghiệm là x = 0,6 . Tính giá trị của m chính xác đến 4 chữ số thập phân
3) TÝnh gi¸ trÞ cña biÓu thøc:
Bµi 1: Cho ®a thøc P(x) = x15 -2x12 + 4x7 - 7x4 + 2x3 - 5x2 + x - 1
 TÝnh P(1,25); P(4,327); P(-5,1289); P()
H.DÉn:
- LËp c«ng thøc P(x) 
- TÝnh gi¸ trÞ cña ®a thøc t¹i c¸c ®iÓm: dïng chøc n¨ng 
- KÕt qu¶: P(1,25) = ; P(4,327) = 
 P(-5,1289) = ; P() =
Bµi 2: TÝnh gi¸ trÞ cña c¸c biÓu thøc sau:
P(x) = 1 + x + x2 + x3 +...+ x8 + x9 t¹i x = 0,53241
Q(x) = x2 + x3 +...+ x8 + x9 + x10 t¹i x = -2,1345
H.DÉn:
- Áp dông h»ng ®¼ng thøc: an - bn = (a - b)(an-1 + an-2b +...+ abn-2 + bn-1). Ta cã:
P(x) = 1 + x + x2 + x3 +...+ x8 + x9 = 
Tõ ®ã tÝnh P(0,53241) = 
T­¬ng tù: 
Q(x) = x2 + x3 +...+ x8 + x9 + x10 = x2(1 + x + x2 + x3 +...+ x8) = 
Tõ ®ã tÝnh Q(-2,1345) = 
Bµi tập: TÝnh gi¸ trÞ biÓu thøc: 
a. A(x) = khi x = 1,23456
b. khi x = 2,18567
c. Q(x) = 1 + x + x2 + x3 +...+ x14 + x15 t¹i x = 1,21
d. R(x) = x2 + x3 +...+ x14 + x15 t¹i x = -2,567
4/ X¸c ®Þnh ®a thøc & tÝnh gi¸ trÞ mét sè gi¸ trÞ cña ®a thøc khi biÕt mét sè gi¸ trÞ kh¸c cña nã:
*Ph­¬ng ph¸p: 	1). Gi¶i hÖ ph­¬ng tr×nh tõ ®ã t×m ®­îc c¸c hÖ sè
	 2). T×m ®a thø phô tr­íc, råi quay l¹i t×m ®a thøc.
 Ví duï: Cho ña thöùc P(x)=x3+ax2+bx+c vaø cho bieát P(1)=4, P(-2)=7, P(3)=12. 
a/ Xác định đa thức P(x).
b/ Tính P(12), P(30).
 Giaûi: Cách 1 : P(1)=4 => 13+a.12+b.1+c =4
 P(-2)=7=> (-2)3+a.(-2)2+b.(-2)+ c = 7
 P(3)=12=> 33+a.32+b.3 + c = 12
Ta có hệ phương trình : 
Giải hệ phương trình 3 ẩn : bấm máy MODE về EQN bấm 3
Sau đó nhập các hệ số a,b,c,d ( hệ số bên vế phải) vào máy
KQ : a = -1; b = -5; c = 9
Vậy P(x)=x3- x2 - 5x + 9 
Sau đó Tính P(12), P(30) ?
Caùch 2 : Ta thaáy :
 P(1)=4=11+3 ; P(-2)=7=(-2)2+3; P(3)=12=(3)2+3
 Xeùt ña thöùc Q(x)=P(x)-(x2+3) = P(x)-x2-3
 Deã thaáyQ(1)=Q(-2)=Q(3)=0. Suy ra x=1, -2, 3 laø nghieäm cuûa Q(x)
 Q(x)=(x-1)(x+2)(x-3)=P(x)-x2-3
 Vì vaäy P(x)=(x-1)(x+2)(x-3)+x2+3
Nhaân ña thöùc vôùi ña thöùc ta tính ñöôïc : P(x)=x3- x2 - 5x + 9 
 Töø ñoù tính ñöôïc P(12), P(30)?
Baøi taäp :
Bài 1 : Cho P(x) = x5 + ax4 + bx3 + cx2 + dx + f . 
Biết P(1) = 1 , P(2) = 4 , P(3) = 9 , P(4) = 16 , P(5) = 15 . Tính P(6) , P(7) , P(8) , P(9)
Giải: 
Ta có P(1) = 1 = 12; P(2) = 4 = 22 ; P(3) = 9 = 32 ; P(4) = 16 = 42 ; P(5) = 25 = 52
Xét đa thức Q(x) = P(x) – x2.
Dễ thấy Q(1) = Q(2) = Q(3) = Q(4) = Q(5) = 0.
Suy ra 1; 2; 3; 4; 5 là nghiệm của đa thức Q(x).
Vì hệ số của x5 bằng 1 nên Q(x) có dạng:
Q(x) = (x – 1)(x – 2)(x – 3)(x – 4)(x – 5).
Vậy ta có Q(6) = (6 – 1)(6 – 2)(6 – 3)(6 – 4)(6 – 5) = P(6) - 62
Hay P(6) = 5! + 62 = 156.
Q(7) = (7 – 1)(7 – 2)(7 – 3)(7 – 4)(7 – 5) = P(7) – 72
Hay P(7) = 6! + 72 = 769
Bài 2:Cho Q(x) = x4 + mx3 + nx2 + px + q . Biết Q(1) = 5 , Q(2) = 7 , Q(3) = 9 , Q(4) = 11 .
a/ Xác định đa thức Q(x).
b/Tính các giá trị của Q(10) , Q(11) , Q(12) , Q(13) 
Hướng dẫn 
Caùch 1 : Ñöa veà heä phöông trình 4 aån :
 giaûi heä phöông trình tìm ñöôïc m = -10; n = 35; p = -48
Thay vaøo tìm q = 4 -m – n - p = 4 – (-10) -35 –(-48) = 27
Q(x) = x4 -10x3 + 35x2 -48x + 27 . 
Caùch 2 : Q(1) = 5 = 2.1 + 3; Q(2) = 7 = 2.2 + 3; Q(3) = 9 = 2.3 + 3 ; Q(4) = 11 = 2.4 + 3
Xét đa thức Q1(x) = Q(x) – (2x + 3)
Bài 3 : Cho P(x) = x5 + ax4 + bx3 + cx2 + dx + e . 
Biết P(1) = 3 , P(2) = 9 , P(3) = 19 , P(4) = 33 , P(5) = 51 . Tính P(6) , P(7) , P(8) , P(9) , P(10) , P(11) . 
Bài 4: Cho P(x) = x4 + ax3 + bx2 + cx + d. Có P(1) = 0,5 ; P(2) = 2 ; P(3) = 4,5 ; P(4) = 8.
a/ Xác định đa thức P(x).
b/ Tính P(2002), P(2003)
Bài 5:Cho P(x) = x4 + ax3 + bx2 + cx + d. Biết P(1) = 5; P(2) = 14; P(3) = 29; P(4) = 50. 
a/ Xác định đa thức P(x). 
b/ Hãy tính P(5) , P(6) , P(7) , P(8)
Bài 6:Cho P(x) = x4 + ax3 + bx2 + cx + d. Biết P(1) = 0; P(2) = 4 ; P(3) = 18 ; P(4) = 48. 
a/ Xác định đa thức P(x).
b/Tính P(2007)
Bài 7 : Cho P(x) = x5 + 2x4 – 3x3 + 4x2 – 5x + m . 
Tìm số dư trong phép chia P(x) cho x – 2,5 khi m = 2003 .
Tìm giá trị của m để P(x) chia hết cho x – 2,5 
P(x) có nghiệm x = 2 . Tìm m . 
Bài 8: Cho P(x) = .
Tìm biểu thức thương Q(x) khi chia P(x) cho x – 5.
Tìm số dư của phép chia P(x) cho x – 5 chính xác đến 3 chữ số thập phân.
Bài 9:Tìm số dư trong phép chia đa thức x5 – 7,834x3 + 7,581x2 – 4,568x + 3,194 cho 
x – 2,652. Tìm hệ số của x2 trong đa thức thương của phép chia trên.
Bài 10:Khi chia đa thức 2x4 + 8x3 – 7x2 + 8x – 12 cho x – 2 ta được thương là đa thức Q(x) có bậc là 3. Hãy tìm hệ số của x2 trong Q(x)
Bài 11:Cho đa thức P(x) = 6x3 – 7x2 – 16x + m .
Tìm m để P(x) chia hết cho 2x + 3
Với m tìm được ở câu a ) , hãy tìm số dư r khi chia P(x) cho 3x – 2 và phân tích P(x) thành tích của các thừa số bậc nhất
Tìm m và n để Q(x) = 2x3 – 5x2 – 13x + n và P(x) cùng chia hết cho x – 2 .
Với n tìm được ở trên , hãy phân tích Q(x) ra tích của các thừa số bậc nhất.
Bài 12: Cho P(x) = x4 + 5x3 – 4x2 + 3x + m và Q(x) = x4 + 4x3 - 3x2 + 2x + n .
Tìm các giá trị của m và n để P(x) và Q(x) cùng chia hết cho x – 2 .
Với giá trị của m và n tìm được , chứng tỏ rằng R(x) = P(x) – Q(x) chỉ có một nghiệm duy nhất
Bài 13 : Cho f(x) = x3 + ax2 + bx + c . Biết : f = ; f = ; f = . 
Tính giá trị đúng và gần đúng của f . 
Bài 14: Xác định các hệ số a, b, c của đa thức:
P(x) = ax3 + bx2 + cx – 2007 để sao cho P(x) chia cho (x – 13) có số dư là 1, chia cho (x – 3) có số dư là là 2, và chia cho (x – 14) có số dư là 3
(Kết quả lấy với hai chữ số ở hàng thập phân)
Bài 15:Xác định các hệ số a, b, c, d và tính giá trị của đa thức 
Q(x) = x5 + ax4 + bx3 + cx2 + dx – 2007 tại các giá trị của x = 1,15; 1,25; 1,35; 1,45
Bài 16: Tìm các hệ số a, b, c của đa thức P(x) = ax3 + bx2 +cx – 2008 biết rằng khi chia P(x) cho nhị thức ( x – 25) thì dư 29542 và khi chia cho tam thức (x2 – 12x + 25) thì có đa thức dư là: 431x – 2933.
HÌNH HOÏC 9
COÂNG THÖÙC TÍNH ÑOÄ DAØI ÑÖÔØNG TROØN
 hay C = 2vì d = 2R.
COÂNG THÖÙC TÍNH ÑOÄ DAØI CUNG TROØN
Vôùi l : laø ñoä daøi cung troøn .
R : Baùn kính ñöôøng troøn .
n : Soá ño ñoä cuûa cung troøn .
COÂNG THÖÙC TÍNH DIEÄN TÍCH HÌNH TROØN 
S = R2. 
•
n0 
A
B
0
R
 COÂNG THÖÙC TÍNH DIEÄN TÍCH HÌNH QUAÏT TROØN 
Dieän tích hình quaït troøn n0
coù hai coâng thöùc :
Vôùi R laø baùn kinh ñöôøng troøn .
 n laø soá ño ñoä cuûa cung troøn .
B
A
O
m
 l laø ñoä daøi cung troøn .
Hình vieân phaân laø phaàn hình troøn giôùi haïn bôûi moät cung vaø cung caêng daây aáy. 
 * Ñeå tính ñöôïc dieän tích hình vie